3. Проверка статистических гипотез

Проблема обнаружения сигнала, несущего информацию, на фоне шумов тесно связана с задачей проверки статистических гипотез в математической статистике. Будем считать, что реализация процесса происходит в дискретные моменты времени. Тогда в нашем распоряжении имеется последовательность случайных величин:

. (3.1)

Реализации шумасчитаем независимыми. Каждая случайная величина (случайный сигнал)принимает значенияиз некоторого множества значений, т.е.

Рассмотрим подробнее проблему принятия решений при проверке гипотез. Под состоянием S источника сигналов будем понимать возможность генерировать один из сигналов или. Если одно из состояний соответствует отсутствию сигнала, скажемS = 0, а другое — состоянию S  0 и требуется определить, в каком состоянии находится источник, то приходим к задаче обнаружения сигналов. Пусть известен закон распределения состояний источника, то есть, с какой вероятностью источник может пребывать в том или ином состоянии, или с какой вероятностью генерируется сигнал в моменты:

. (3.2)

Положим приемник фиксирует реализации случайного сигнала (случайной величины)в моменты времени. В результате имеем набор реализаций=, который называютвыборкой объёма . Каждая реализацияпринадлежит множеству, определенному выше, (). Совокупность случайных величинпринимает значенияиз множества. Все возможные выборки, содержащиеся в этом множество, называютсягенеральной совокупностью. Совместная вероятность ,получить выборку видазависит от состоянияS источника . Эта вероятность, как функция состояния источника, называетсяфункцией правдоподобия. Функция правдоподобия отвечает на вопрос – насколько правдоподобно получить данную выборку при условии, что источник находился в состоянии.

Во время обработки выборочных значений (выборки) производятся определенные операции с ними.Любую функцию от выборки будем называтьстатистикой. Например, статистиками будут среднее от выборки и выборочная дисперсия, соответственно,

, .

Статистика является случайной величиной, так как она – результат обработки какой-то одной совершившейся реализациииз множества возможных случайных реализаций, составляющих множество. В то же время математическое ожидание, дисперсия– не случайные (детерминированные) величины.

Чтобы определить состояние источника, выдвигаются и проверяются гипотезы о том, что источник находится в состоянииили в состоянии. Решение о верности той или иной гипотезы принимается на основе анализа выборок. Ели бы не было шумавсе возможные выборки можно было бы разделить на два непересекающиеся подмножества, одно из которых соответствует состоянию источника- сигнал отсутствует в принятой реализации, другое – состоянию источникасигнал присутствует в принятой реализации.

Разобьем множество выборочных значенийна два подмножестваи(рисунок 3.1). Будем считать, если выборкапринадлежит подмножеству, то источник находится в состоянии. Если, то источник находится в состоянии. Проверку принадлежности выборкитому или иному подмножеству,назовёмправилом принятия решения .

При сложении шума и сигнала, можно ошибочно попасть в область, не соответствующей истинной гипотезе и совершить ошибку при проверке гипотез.

Правила обработки сигнала зависят от целей и требований, на которые рассчитана система. Может существовать несколько правил решения для достижения одной и той же цели. Среди этих правил необходимо выбрать наилучшее в некотором смысле, то есть возникает необходимость в некой функции, определяющей критерий³ качества выбранного правила. Эта функция, достигающая экстремального значения при некоторых условиях, называется критерием принятия решений, или критерием оптимальности.

Рассмотрим пример 3.1. Пусть источник имеет два возможных состояния . Случайная величинаможет принимать два значения — 0 и 1.

Произведено четыре испытания . Генеральная совокупность состоит из различных четырёхразрядных двоичных кодов, общее число которых в данной задаче составляет. Рассмотрим возможные правила принятия решения о состоянии источника. На рисунке 3.2 изображены возможные правила разбиения множества реализаций на подмножестваи. Согласно правилуподмножествосоставлено из двух комбинаций. Все остальные комбинации принадлежат подмножеству. По правилувыборочное пространстворазделено на подмножестваитаким образом, чтосодержит все возможные реализации , а все остальные реализации составляют подмножество. Предложенные правила разбиения множествана подмножестваисубъективны.

Если выборка попадает в область, принимается решениео том, что источник находится в состоянии, т.е. верна гипотеза. Если выборка принадлежит области, принимается решениео том, что источник находится в состоянии.

Если состояние источника S зависит только от одного значения параметра, то проверяемая гипотеза H относительно этого параметра будет простой гипотезой. Если же состояние источника зависит более чем от одного значения параметра, то проверяемая гипотеза H относительно этих параметров будет сложной гипотезой.

Например, состояние источника характеризуется амплитудой напряжения s₀ = 1 V. Гипотеза H о том, что напряжение источника равно 1 вольту, будет простой гипотезой. Но если состояние характеризуется некоторым конечным множеством значений тех же амплитуд, скажем s₀[12), гипотезаH, о том, что напряжение источника может принадлежать интервалу значений от 1 вольта до 2 вольт, будет сложной гипотезой.

Если число гипотез равно двум (), то процедура проверки этих гипотез называетсядвухальтернативной. Если же число гипотез более двух, то процедура проверки совокупности этих гипотез является многоальтернативной.

В дальнейшем понадобится отношение двух функций правдоподобия

, (3.3)

являющейся функцией выборочных значений , и, следовательно, является реализацией некоторой случайной величинысо значениями. Ввиду того, что отношение правдоподобия является функцией от выборки, то она также является статистикой. Отношение правдоподобия «отображает точкуиз многомерного пространства в одномерное с неотрицательными значениями на действительной оси» (Левин Б.Р.).

Если выборочные значения принадлежат непрерывному множеству, описываемому распределением плотности вероятности, то отношение правдоподобия (3.3) примет вид

. (3.4)

Рассмотрим два примера.

Пример 3.2. Пусть случайная величина принимает два значения

но вероятность зависит от состояния источника, и примем:

- в состоянии источника — вероятность генерации символа «1» равна,

- в состоянии источника — вероятность генерации символа «1» равна,.

Произвели N независимых испытаний, в результате которых получили последовательность из нулей и единиц. Пусть в этой последовательности содержится m единиц. Тогда отношение правдоподобия по выражению (3.3) имеет вид

или

. (3.5)

В этом примере множество случайных величин , реализованных в виде выборкии обладающих совместной вероятностью, при помощи статистикипереведено в одномерную случайную величину. Реализацией случайной величиныявляется числоm – сумма числа единиц в выборке объёма N. Распределение суммы числа единиц (одномерная величина) и его числовые характеристики зависят от состояния источника (от вероятностей и).

Пример 3.3. Пусть случайная величина распределена по нормальному закону

. (3.6)

Математическое ожидание зависит от состояния источника. Примем

, если источник в состоянии ,

, если источник в состоянии .

Производится N независимых испытаний и реализуется выборка вида . Совместная плотность распределения вероятности выборки в зависимости от состояния источника равна

. (3.7)

Используя (3.4), запишем отношение правдоподобия

==

= =

=.

Логарифмируя предыдущее выражение, получим

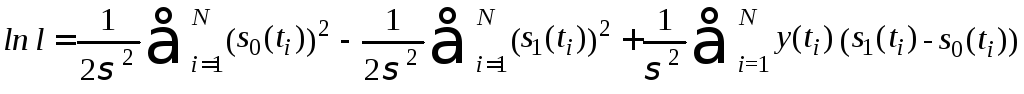. (3.8)

В этом выражении суммы отображают многомерные величины в одномерные величины. Сумма, содержащая реализацию , определяет новую случайную величинус определенным законом распределения плотности вероятности (сумма нормально распределенных случайных величин распределена по нормальному закону) и числовыми характеристиками, зависящими от состояния источника.