Упругие свойства минералов и горных пород Упругие параметры физических тел

Упругость – свойство вещества оказывать влияющей на него силе механическое сопротивление и принимать после её спада исходную форму.

При упругих деформациях вещество восстанавливает свои первоначальные объем и форму после прекращения действия сил, вызывающих их деформацию. В простейших случаях малых деформаций зависимость линейная – и действует закон Гука, на котором основана теория упругости. Согласно этой теории малые деформации пропорциональны приложенной нагрузке:

где Δl/lиΔd/d–относительная продольная и поперечная деформация;- приложенная к телу нагрузка в кг,S – площадь поперечного сечения тела в м²;/S – напряжение.

Количественными характеристиками упругих свойств являются модули упругости.

1. модуль Юнга E (модуль продольной упругости) – это отношение нормального напряжения к относительному удлинению, вызванному этим напряжением в направлении его действия. Модуль Юнга характеризует способность тел сопротивляться деформации растяжения или сжатия:

, где p– нормальное растяжение,- относительное удлинение.

Единица измерения модуля Юнга в системе СИ: Па (паскаль), в системе СГС дин/см².

2) коэффициент Пуассона σ_П (коэффициент поперечного сжатия) – отношение поперечного сжатия тела при одноосном растяжении к продольному удлинению. Коэффициент Пуассона равен абсолютному значению отношения относительной поперечной деформации тела к относительной продольной деформации:

,,

где ε_x , ε_y , ε_z – деформации по соответствующим осям.

В твердых породах коэффициент Пуассона изменяется от 0,1- до 0,4. Чем больше значение коэффициента Пуассона, тем больше порода может деформироваться. Более однородные по минеральному составу породы характеризуются более низкими значениями коэффициента Пуассона.

3. константы Ламе λ:

, где K модуль объемного сжатия.

3. модуль сдвига G. Модуль сдвига определяет способность тел сопротивляться изменению формы при сохранении их объема:

, где r– касательное напряжение;α– угол сдвига.

Модуль сдвига численно равен другой константе Ламе:

В телах под действием механических напряжений возникают деформации и генерируются разные по природе упругие колебания (волны) продольные pи поперечныеs. Продольные волны являются результатом деформации типа сжатия – растяжения, поперечные – сдвига. В свободных газах и жидкостях возникают только продольные волны и отсутствуют поперечные.

Скорость упругих волн равна отношению длины пути соответствующей волны к времени пробега этого пути:

;

Для геофизиков большое значение имеют скорости, которые связаны с модулями упругости и плотностью.

Скорость продольных упругих волн или упругих колебаний, возникающих вследствие деформаций растяжение-сжатие в любой среде:

Скорость поперечных волн или упругих колебаний, возникающих вследствие деформаций сдвига в твердой среде:

Скорости v_pиv_s в принципе независимые величины. Связь между ними осуществляется через коэффициент Пуассона:

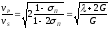
При сейсморазведочных работах вычисляют ряд скоростных параметров разреза: граничную, пластовую, среднюю, эффективную и лучевую скорости.

Распространение упругих колебаний сопровождается затуханием их амплитуды по мере удаления от источника. Амплитуда Aгармонической волны с частотойwубывает с расстояниемl в однородной поглощающей среде по закону:

,

где A₀– амплитуда волны в некоторой фиксированной (начальной) точке;n - показатель расхождения фронта волны;α– коэффициент поглощения.

Коэффициент поглощения динамическая характеристика упругих сред и измеряется в м^-1. Коэффициент поглощения упругих колебаний зависит от свойств среды. Чем ниже скорость распространения упругих колебаний в породе, тем выше значение коэффициента поглощения. С увеличением пористости коэффициент поглощения растет.