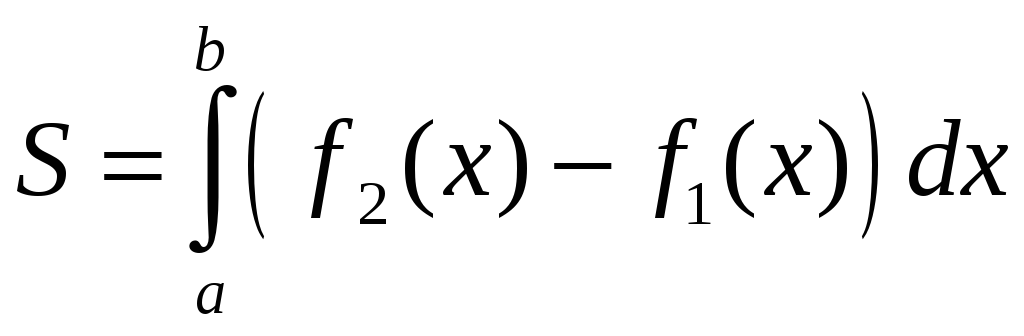Лекция (Интегралы)

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

Первообразная функция. Понятие неопределенного интеграла.

Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу — нахождение самой функции по ее производной или дифференциалу.

Функция называется первообразной функцией для функции на промежутке , если в каждой точке этого промежутка .

Например, 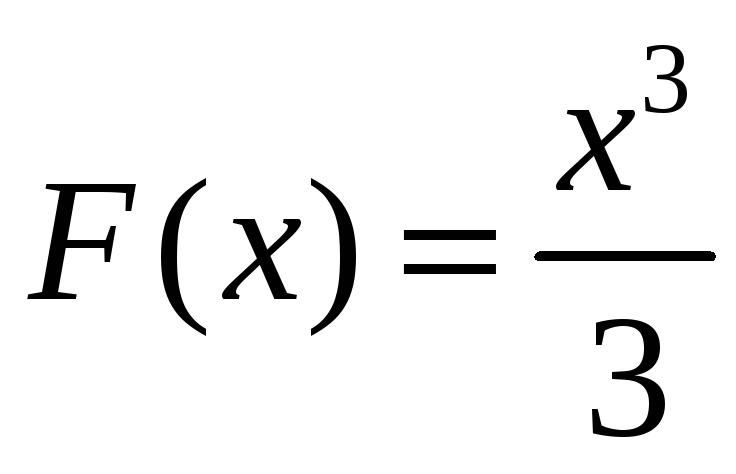является первообразной для функции , так как .

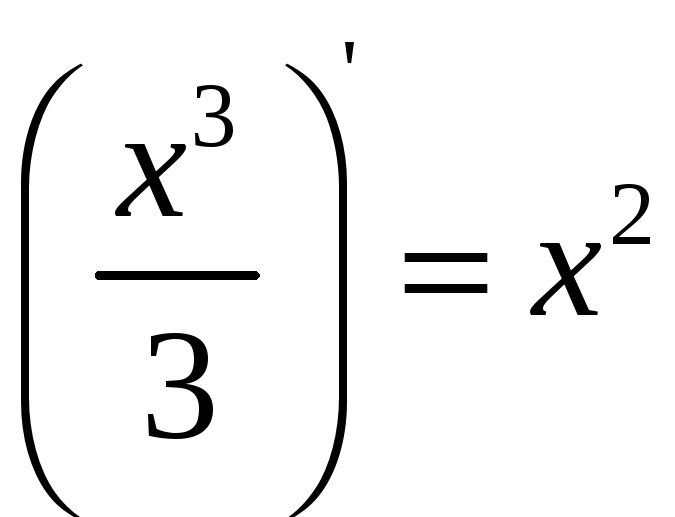Следует отметить, что для заданной функции ее первообразная определена неоднозначно. Дифференцируя, нетрудно убедиться, что все функции 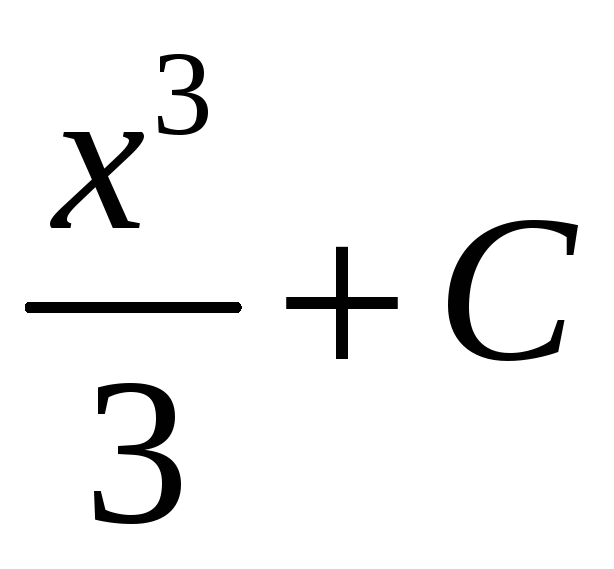, где — некоторое число, являются первообразными для функции .

Аналогично в общем случае, если — некоторая первообразная для , то, поскольку , функции вида , где - произвольное число, также являются первообразными для .

Совокупность всех первообразных для функции на промежутке называется неопределенным интегралом от функции и обозначается , где — знак интеграла, — подынтегральная функция, — подынтегральное выражение. Таким образом,

где — некоторая первообразная для , — произвольная постоянная.

Например, - первообразная для функции , то .

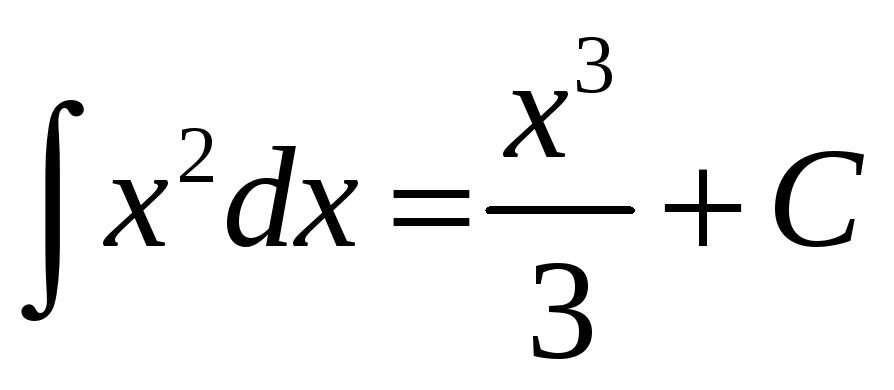Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.

Основные свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е,

.

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.

.

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

где — произвольное число.

4. Постоянный множитель можно выносить за знак интеграла, т.е.

где — произвольное число.

5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.

Перечислим интегралы от элементарных функций, которые в дальнейшем мы будем называть табличными:

.

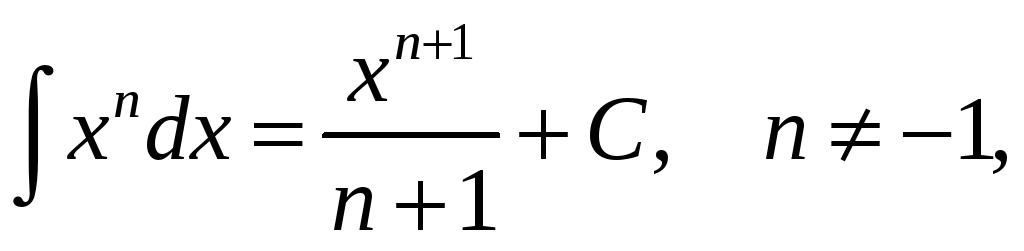
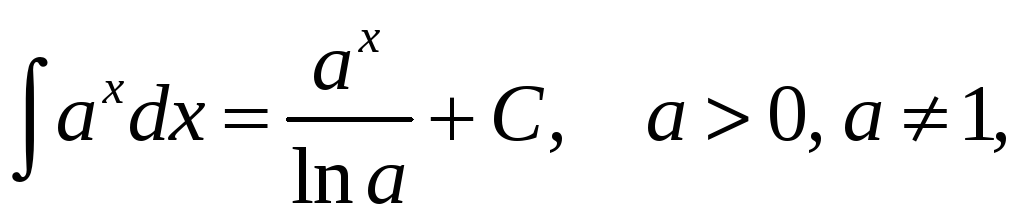
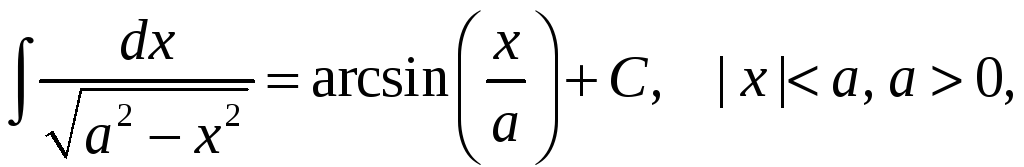
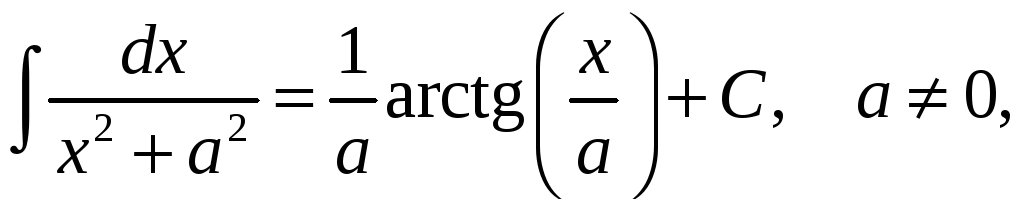
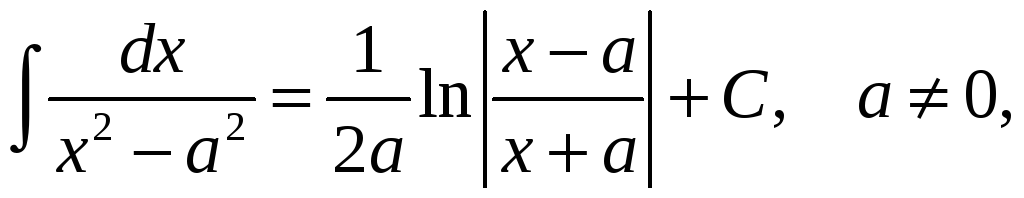
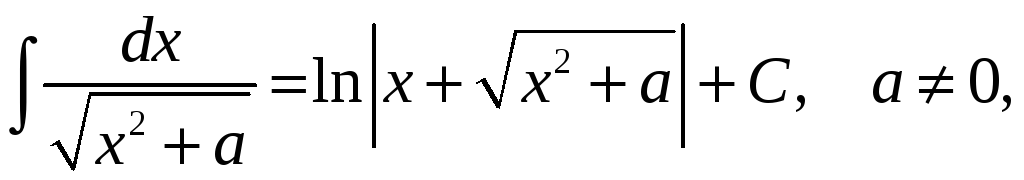
Пример . Найти .

Решение.

=.

Интегрирование заменой переменных (подстановкой).

Одним из основных методов интегрирования является метод замены переменной (или метод подстановки), описываемый следующей формулой:

где — функция, дифференцируемая на рассматриваемом промежутке.

Пример. Найти .

Решение.

.

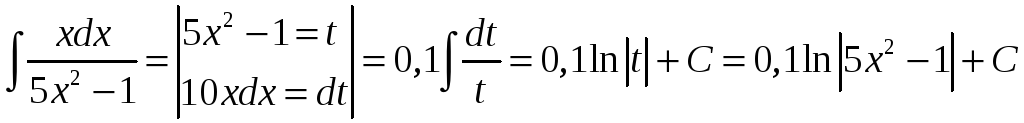Следует отметить, что новую переменную можно не выписывать явно (в таких случаях говорят о преобразовании функции под знаком дифференциала или о введении постоянных и переменных под знак дифференциала). Например,

Тогда

Пример . Найти .

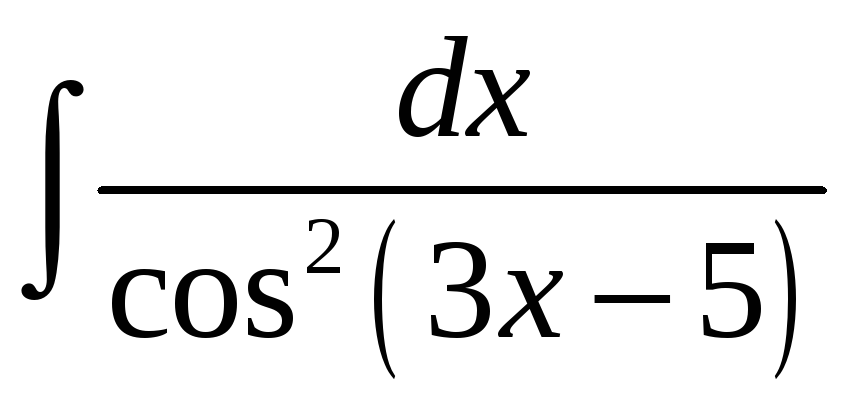Решение.

.

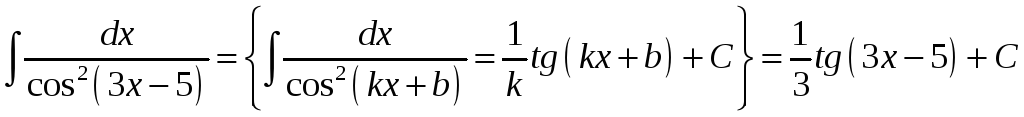Интегрирование по частям.

Пусть и — дифференцируемые функции. По свойству дифференциала

или

.

Интегрируя левую и правую части последнего равенства, получаем формулу интегрирования по частям для неопределенного интеграла

.

Пример . Найти .

Решение.

.

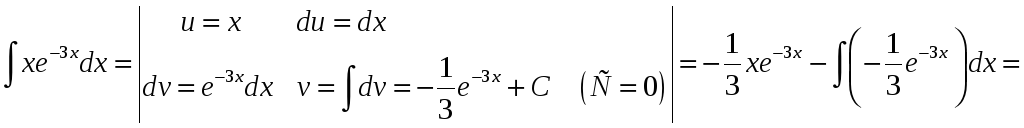
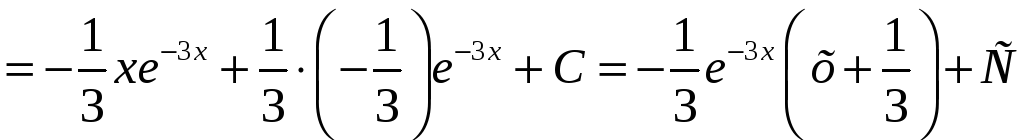Пример . Найти .

Решение.

.

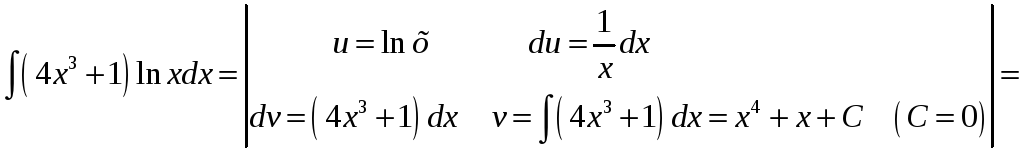
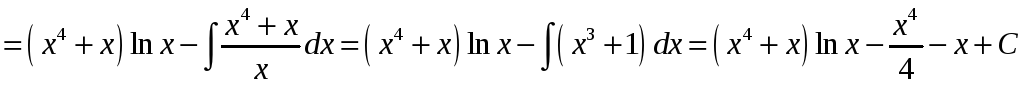Пример. Найти .

Положим Тогда и Применяя формулу интегрирования по частям, получаем

Повторное применение формулы интегрирования по частям приводит к табличному интегралу. Действительно, положим теперь Тогда Следовательно,

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

Задача о площади криволинейной трапеции. Пусть на отрезке задан неотрицательная функция . Требуется найти площадь криволинейной трапеции, ограниченной кривой , прямыми , и осью абсцисс .

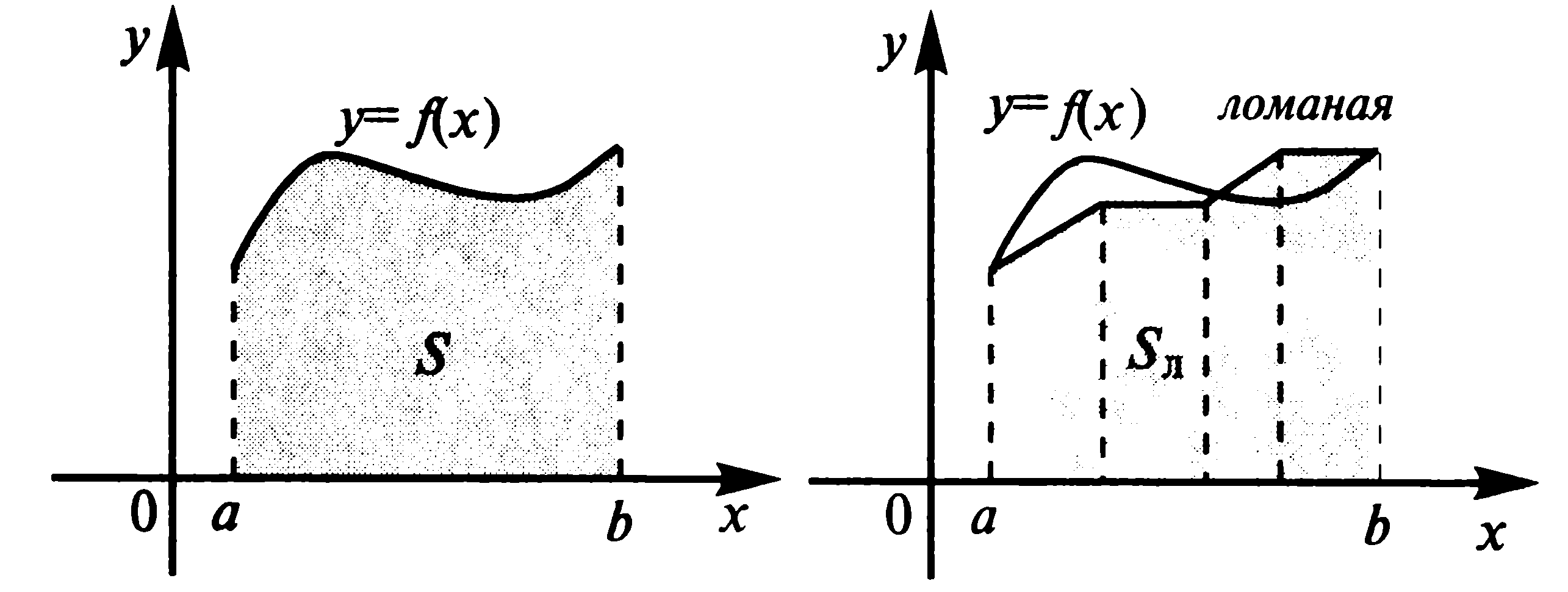
Наметим общий подход к решению этой задачи. Введем в рассмотрение некоторую ломаную, которая расположена достаточно близко к кривой на . Фигура под ломаной состоит из трапеций (прямоугольников), и ее площадь (равная сумме площадей этих трапеций) может быть вычислена с использованием известных формул планиметрии. Поскольку ломаная выбрана достаточно близко к кривой , то справедливо приближенное равенство . Это равенство оказывается тем более точным, чем ближе расположена ломаная к исходной кривой. Поэтому естественно за искомую площадь взять предел площади под ломаной в предположении неограниченного приближения ломаной к заданной кривой.

Понятие интегральной суммы. Пусть на задана функция . Разобьем отрезок на элементарных отрезков точками : .

На каждом отрезке разбиения выберем некоторую точку и положим , где . Сумму вида

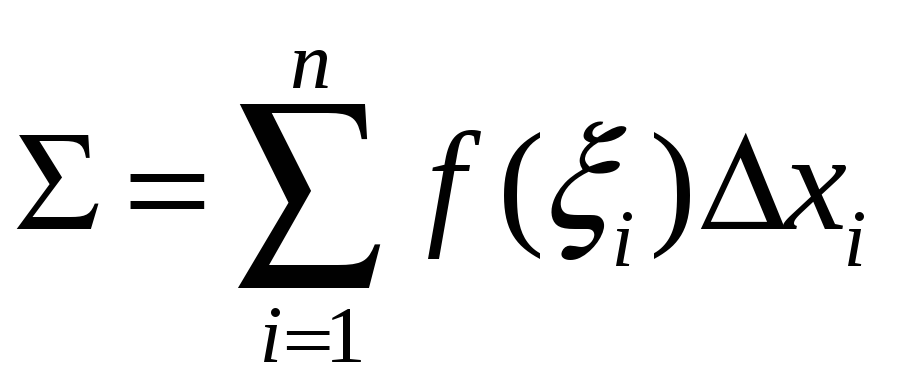
будем называть интегральной суммой для функции на .

Очевидно, что интегральная сумма зависит как от способа разбиения отрезка точками , так и от выбора точек на каждом из отрезков разбиения , .

Геометрический смысл интегральной суммы состоит в том, что она равна площади под ломаной, образованной на каждом из отрезков прямой , параллельной оси абсцисс.

Для избранного разбиения отрезка на части обозначим через максимальную из длин отрезков , где.

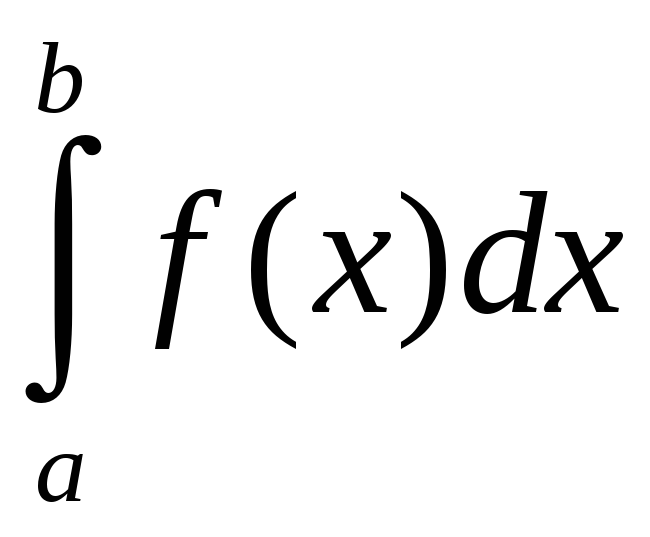Пусть предел интегральной суммы при стремлении к нулю существует, конечен и не зависит от способа выбора точек ,... и точек . Тогда этот предел называется определенным интегралом от функции на , обозначается , а сама функция называется интегрируемой на отрезке , т.е.

.

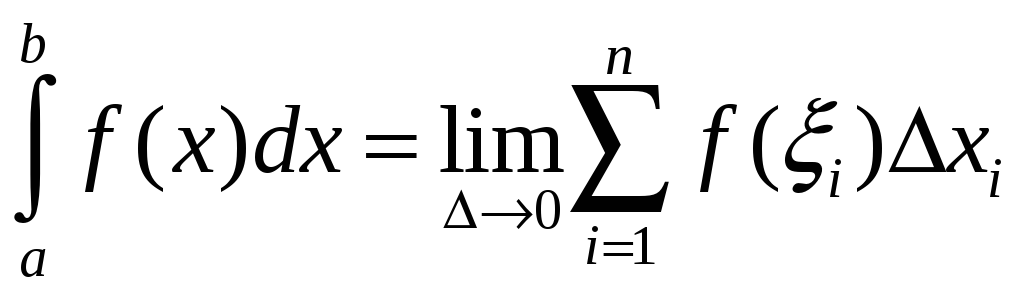При этом число называется нижним пределом, число — его верхним пределом; функция — подынтегральной функцией, выражение - подынтегральным выражением, а задача о нахождении 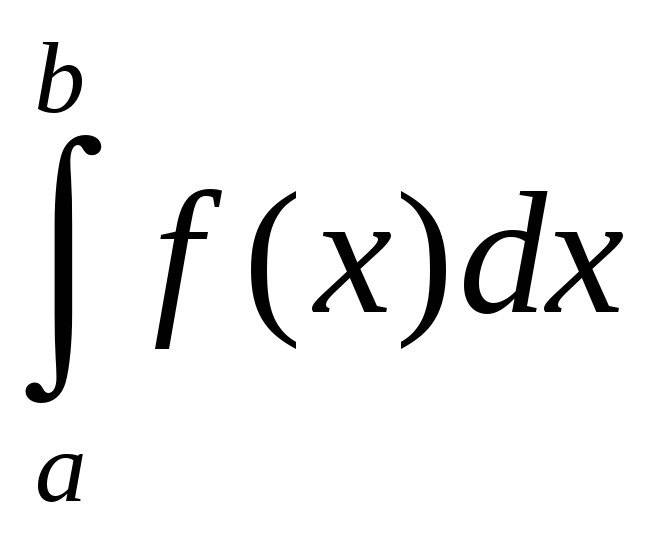— интегрированием функции на отрезке .

Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы существенно различные понятия: в то время как представляет семейство функций, 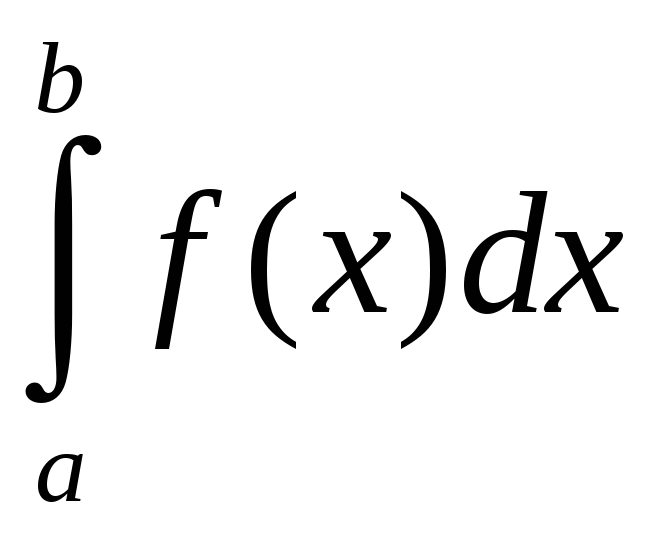есть определенное число.

Во введенном определении определенного интеграла 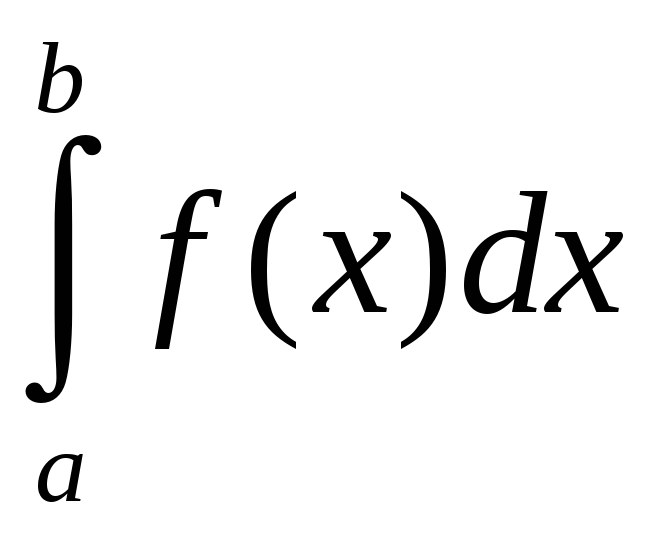предполагается, что . По определению положим

.

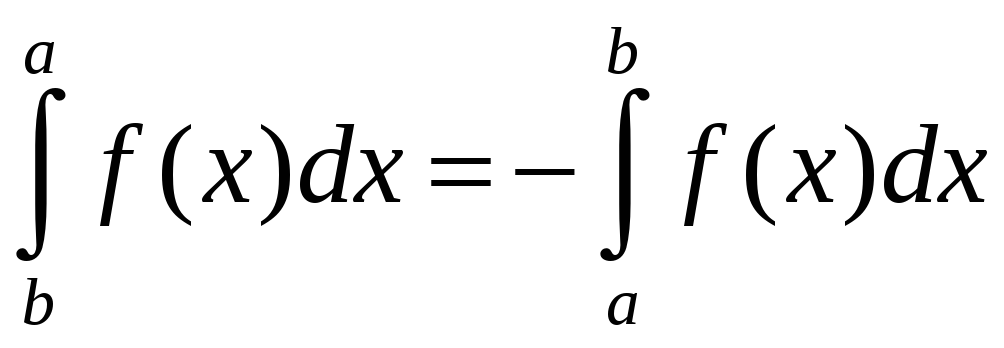Геометрический смысл определенного интеграла. Понятие определенного интеграла введено таким образом, что в случае, когда функция неотрицательна на отрезке , где , 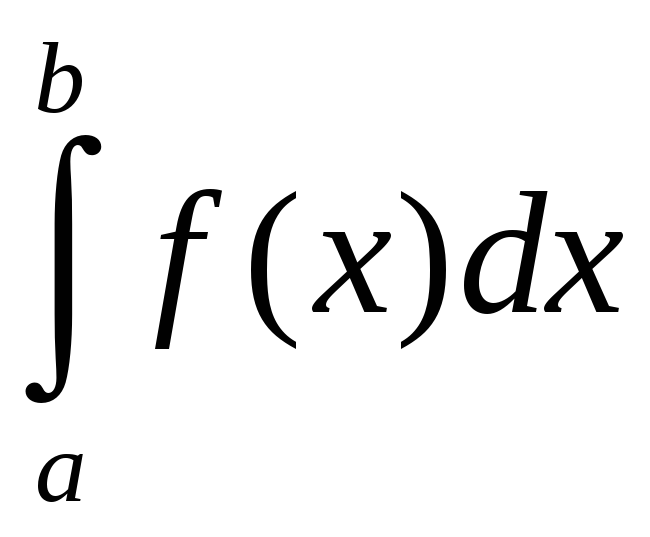численно равен площади под кривой на .

Теорема. (Достаточное условие существования определенного интеграла)

Если функция непрерывна на отрезке , то она интегрируема на этом отрезке.

Свойства определенного интеграла.

1. Постоянный множитель можно выносить за знак интеграла, т.е.

2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е.

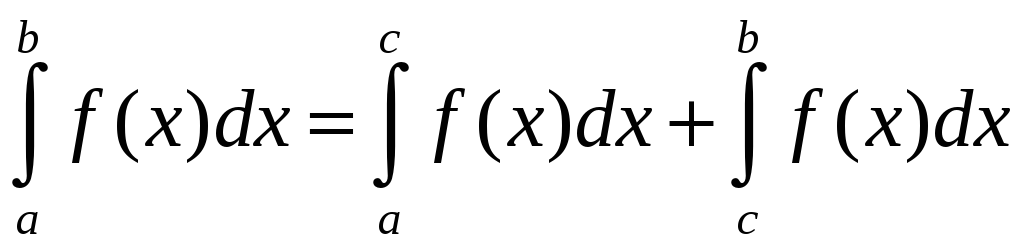
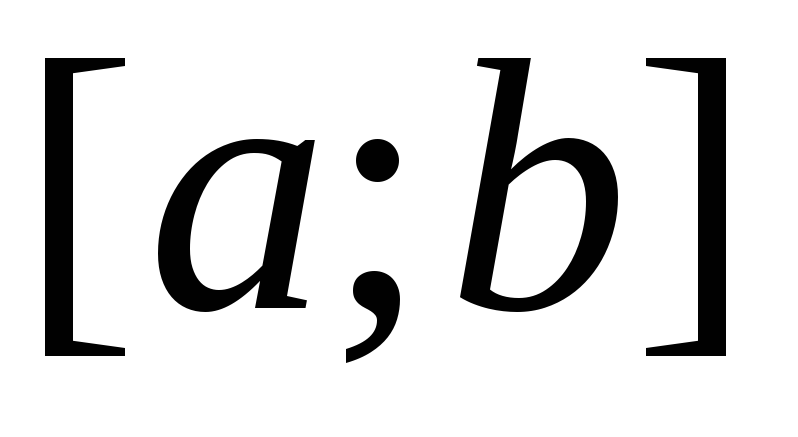
4. Если на отрезке 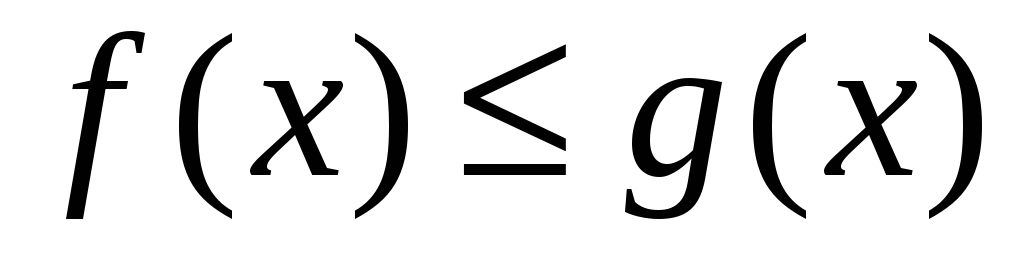, то и

,

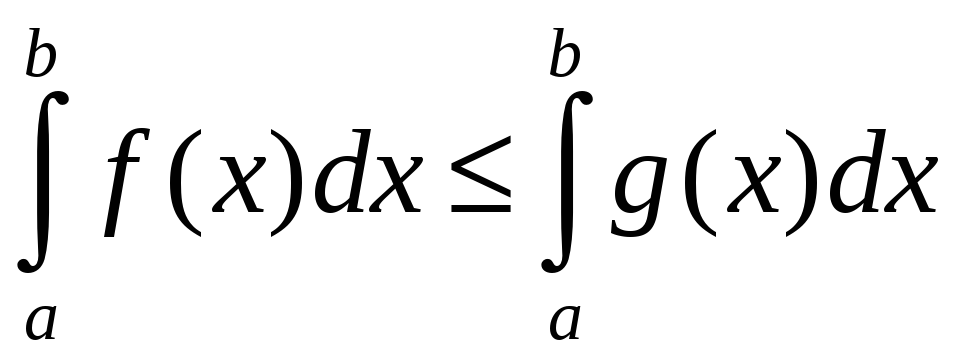т.е. обе части неравенства можно почленно интегрировать.

Основная теорема интегрального исчисления – формула Ньютона-Лейбница.

Теорема. Пусть функция непрерывна на отрезке и — любая первообразная для на . Тогда определенный интеграл от функции на равен приращению первообразной на этом отрезке, т.е.

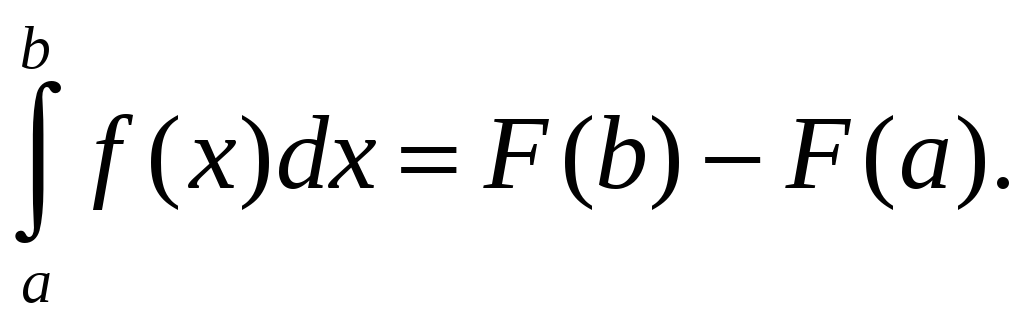
Нахождение определенных интегралов с использованием формулы Ньютона—Лейбница осуществляется в два шага: на первом шаге, используя технику нахождения неопределенного интеграла, находят некоторую первообразную для подынтегральной функции ; на втором применяется собственно формула Ньютона—Лейбница — находится приращение первообразной, равное искомому интегралу. В связи с этим введем обозначение для приращения первообразной, которое удобно использовать при записи решений. По определению положим

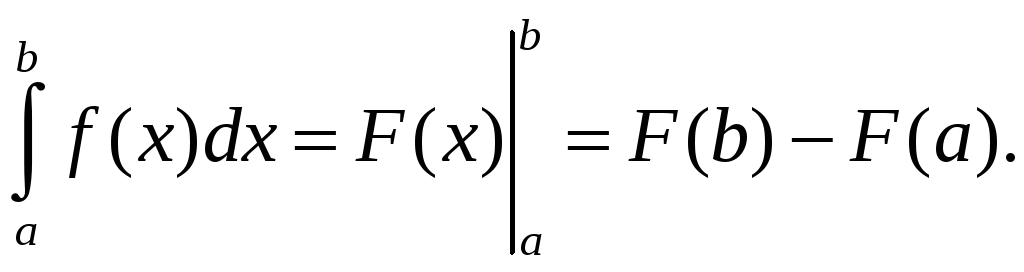
Вычисление определенного интеграла заменой переменных и по частям.

Теорема. Пусть функция имеет непрерывную производную на отрезке , , и функция непрерывна в каждой точке вида , где .

Тогда справедливо следующее равенство

Эта формула носит название формулы замены переменной в определенном интеграле.

Теорема. Пусть функции и имеют непрерывные производные на отрезке . Тогда

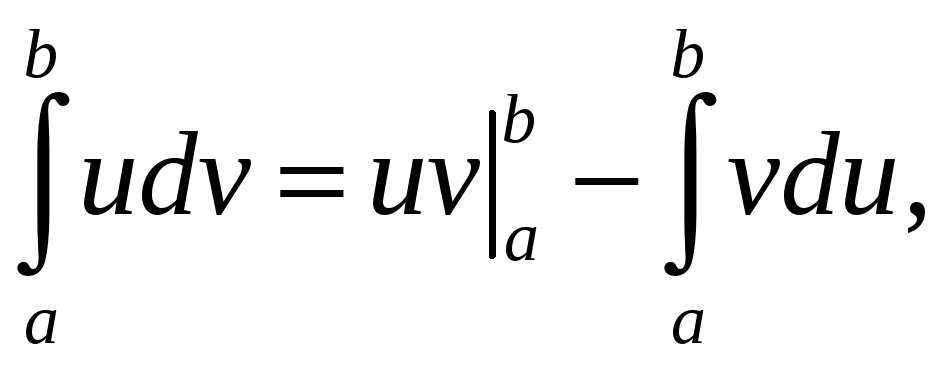где .

Эта формула называется формулой интегрирования по частям для определенного интеграла.

Вычисление площадей плоских фигур.

Пусть функция неотрицательна и непрерывна на отрезке . Тогда по геометрическому смыслу определенного интеграла площадь под кривой на численно равна определенному интегралу 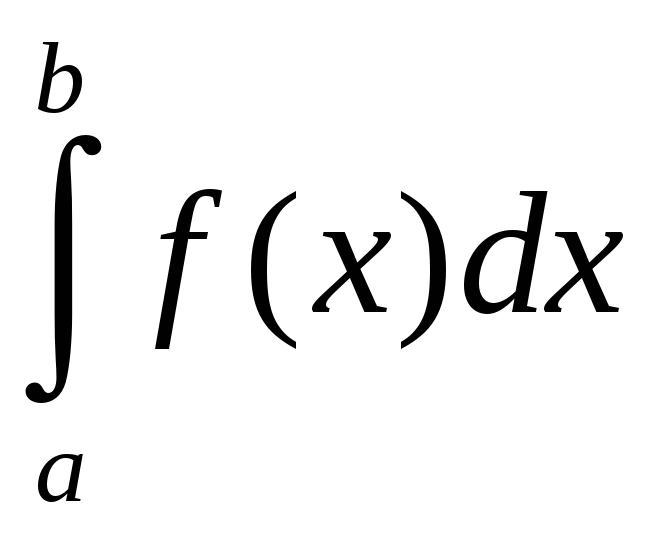, т.е. .

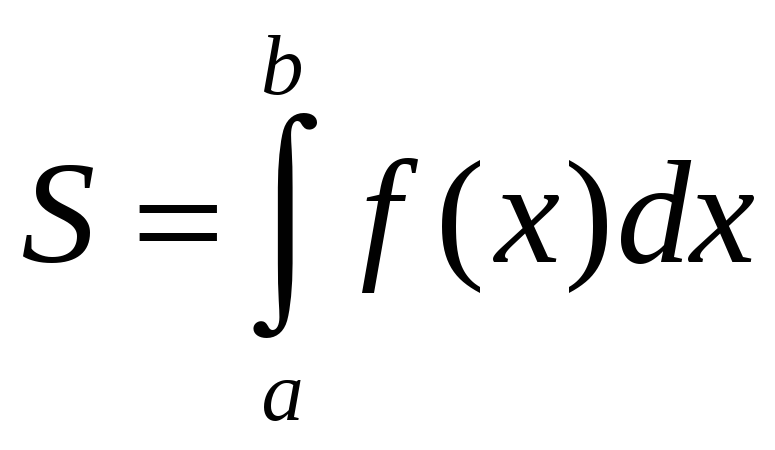Теорема. Пусть на отрезке заданы непрерывные функции и такие, что . Тогда площадь фигуры, заключенной между кривыми и , на отрезке вычисляется по формуле