8Определение ДИ. Свойства ДИ

РАЗДЕЛ VIII. ДВОЙНЫЕ ИНТЕГРАЛЫ

ЛЕКЦИЯ 1. ДВОЙНОЙ ИНТЕГРАЛ: ОПРЕДЕЛЕНИЕ, СВОЙСТВА, ВЫЧИСЛЕНИЕ В ПДСК

З адача, приводящая к понятию двойного интеграла. Определение двойного интеграла. Тело, ограниченное замкнутой областью плоскости , непрерывной над поверхностью , цилиндрической поверхностью, образующая которой параллельна оси , направляющей служит граница области , называется цилиндрическим (рис. 1). Найдём его объём.

Разобьём цилиндрическое тело на элементарных цилиндрических тел с основаниями ( ) произвольной формы (получим столбики с криволинейным верхом). Площадь каждого основания равна . Одно из элементарных цилиндрических тел выделено цветом на рис. 1.

Ясно, что объём цилиндрического тела равен сумме объёмов элементарных цилиндрических тел:

.

Найдём , заменив элементарное цилиндрическое тело цилиндром с основанием . Высота цилиндра равна значению функции в произвольно выбранной точке области (цилиндр имеет вид столбика с плоским верхом; исходное цилиндрическое тело получит ступенчатую поверхность).

Объём элементарного цилиндрического тела приближённо равен объёму цилиндра. Найдём объём цилиндра, умножив площадь его основания на высоту цилиндра :

.

Понятно, что сумма таких произведений выражает объём ступенчатого цилиндрического тела и приближённо равна объёму данного тела:

.

Сумма называется интегральной Римана функции в области .

Конечный предел последовательности интегральных сумм , , …, , …, составленных для различных разбиений области и различного выбора точки в основании , при и ( – наибольшая из хорд оснований ), называется двойным интегралом функции по области .

Обозначение:

.

Читается: (двойной) интеграл по области эф от икс игрэк дэ эс.

называется областью интегрирования, – подынтегральной функцией, и – переменными интегрирования, – элементом площади.

Другое обозначение

с вязано с возможностью разбиения области произвольным образом (рис. 2), в том числе и прямыми, параллельными осям координат и (рис. 3).

Геометрический смысл двойного интеграла состоит в следующем: двойной интеграл функции по области равен объёму цилиндрического тела с основанием , ограниченного сверху поверхностью .

Свойства двойного интеграла. Определения определённого и двойного интеграла очень похожи, поэтому похожи и их свойства.

1. , где и – константы.

2. Если область интегрирования разбита на две непересекающиеся области и такие что , то

.

3. Если в области , то .

Если в области , то .

4. , так как

,

где – площадь области .

5. Если в области выполняется неравенство , то , где – площадь области .

6. В области существует такая точка , что

,

где – площадь области . Величина называется средним значением функции в области .

Вычисление двойного интеграла в прямоугольных декартовых координатах. Пусть область есть прямоугольник, определяемый неравенствами , , и непрерывна в этом прямоугольнике. Тогда двойной интеграл функции равен объёму тела с основанием , ограниченного сверху поверхностью , с боков – плоскостями , , , :

.

С другой стороны, объём тела по известной площади любого его поперечного сечения (на рис. 4 выделено цветом) находится по формуле , где – площадь сечения данного тела плоскостью, проходящей через точку и перпендикулярной к оси (рис. 4). То есть

.

Так как сечение является криволинейной трапецией, ограниченной сверху графиком функции , где фиксировано, , то по формуле имеем .

Из этих рассуждений следует, что

.

Т аким образом, нахождение двойного интеграла сводится к вычислению двух определённых. При вычислении «внутреннего» интеграла (записанного в квадратных скобках) считается постоянным.

Повторный интеграл можно записать так:

.

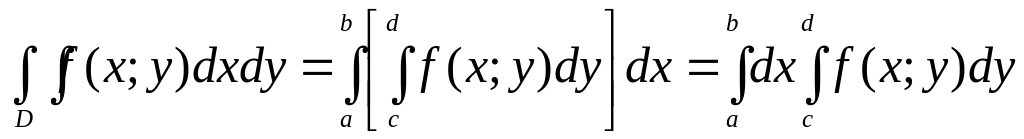Аналогично можно показать, что

,

и записать повторный интеграл следующим образом:

.

Понятно, что

.

Последнее равенство означает, что результат интегрирования не зависит от порядка интегрирования.

► Пример. Вычислить двойной интеграл , где область определяется неравенствами , , в различном порядке интегрирования.

Р ешение. Область построена на рисунке 5.

Первый способ:

.

Второй способ:

. ◄

Рассмотрим случай, когда ограничена слева и справа прямыми , соответственно; снизу и сверху кривыми и соответственно; каждая из которых пересекается с прямыми , только в одной точке (рис. 6).

Т огда в сечении получим криволинейную трапецию, ограниченную линиями , где фиксировано, , , (на рисунке 7 сечение выделено цветом).

Площадь этой трапеции находим с помощью определенного интеграла

.

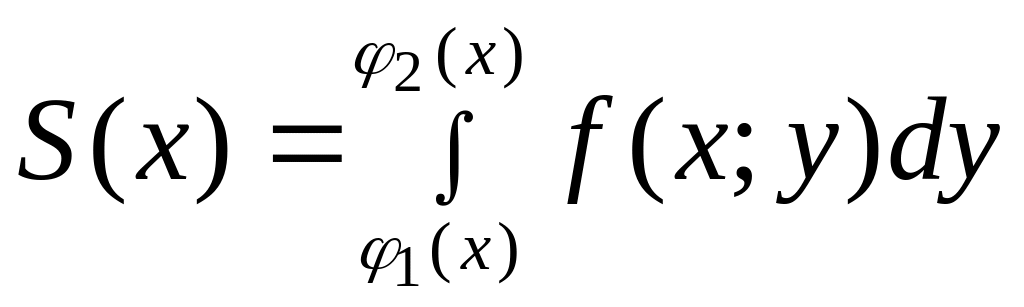Объём цилиндрического тела равен:

.

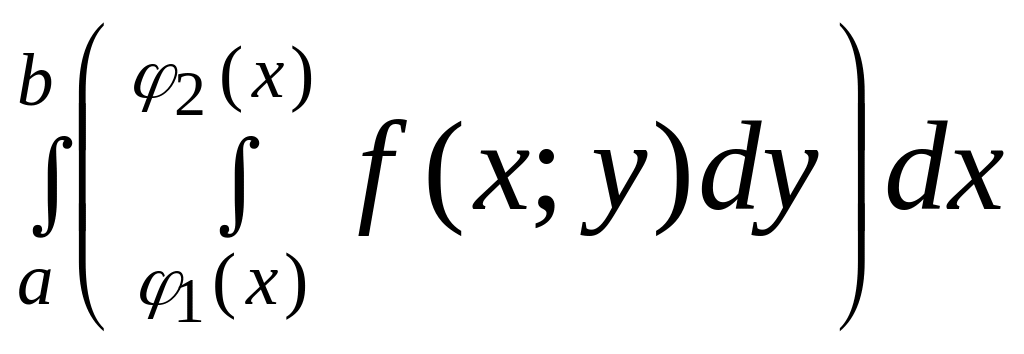Значит,

,

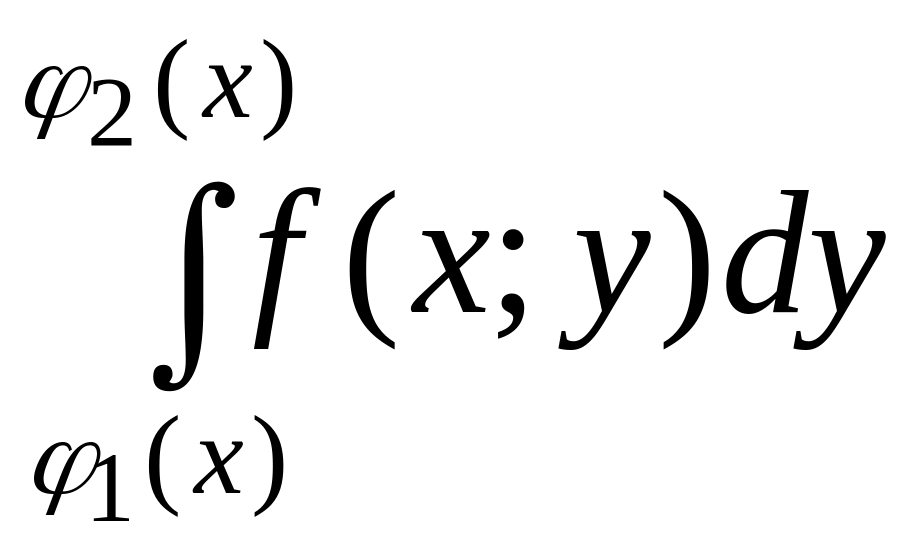г де при вычислении интеграла величину полагают постоянной.

Если область ограничена снизу и сверху прямыми , соответственно; слева и справа кривыми и соответственно; каждая из которых пересекается с прямыми , только в одной точке (рис. 8), то двойной интеграл равен повторному интегралу вида:

,

г де при вычислении интеграла величину полагают постоянной.

Понятно, что

.

► Пример. Вычислить двойной интеграл где область ограничена линиями , .

Решение. Область построена на рисунке 9. Линии , пересекаются в точках и . Полученная область интегрирования является областью первого вида, для которой , , , . Тогда

.

Вычислим сначала внутренний интеграл, стоящий в скобках, считая постоянной величиной:

 =

.

Вычислим внешний интеграл, интегрируя полученную функцию по в пределах от -3 до 3:



.

Итак, . ◄

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Ч то выражает произведение в выражении ?

2. На рисунке 10 показан один из способов уменьшения площади области . Какое требование из определения двойного интеграла не выполняется в этом случае?

3. Выполните рисунки, отражающие свойства 2, 3, 5, 6 двойного интеграла.

4. Двумя способами вычислите по области , ограниченной линиями , , .

7