6Числовые ряды

РАЗДЕЛ IV. РЯДЫ

ЛЕКЦИЯ 1. ЧИСЛОВЫЕ РЯДЫ. РЯД ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ

Для упрощения действий, связанных с интегрированием, Ньютон и Лейбниц выражали подынтегральную функцию в виде многочлена с бесконечным числом слагаемых. Коэффициенты при степенях брались так, чтобы этот многочлен по мере роста порядкового номера слагаемого давал всё более точное значение функции. Например, функцию Ньютон заменял выражением . Если , то слагаемые 1, , , …, образуют бесконечную убывающую геометрическую прогрессию ( , где ), и сумма её равна . Если же , то при сумма не стремится к . Применяя к выражениям функций через многочлены обычные правила алгебры, математики восемнадцатого века сделали множество открытий. Но обнаружилось, что иногда применение этих правил к бесконечным многочленам приводит к ошибкам. Поэтому возникла необходимость в точных формулировках понятий и строгих доказательствах свойств бесконечных многочленов. Эта проблема решена математиками в девятнадцатом веке.

Раздел математики, позволяющий решить любую корректно поставленную задачу с достаточной для практического использования точностью, называется теорией рядов.

Понятие числового ряда. Пусть дана бесконечная последовательность чисел

, где , .

Определение 1.1. Числовым рядом называется сумма членов числовой последовательности:

, (1)

где числа , , …, , – члены числового ряда, – общий член ряда (правило, по которому каждому номеру ставится в соответствие определенное значение функции ).

Если известен общий член ряда , то ряд считается заданным. Например, ряд не задан, так как его общий член не известен, ряд задан: формула описывает его общий член.

Сложим члены числовой последовательности , где , , в данном их порядке:

,

,

,

…,

,

…

Получим новую последовательность .

Определение 1.2. Сумма первых членов ряда (1) называется -ой частичной суммой ряда и обозначается :

.

Например, для числового ряда частичные суммы имеют вид: , , , …, , … . Составим последовательность частичных сумм данного ряда: .

Сходящиеся и расходящиеся числовые ряды

Определение 1.3. Числовой ряд называется сходящимся, если последовательность его частичных сумм имеет конечный предел. Этот предел называется суммой сходящегося ряда:

.

Если же предел последовательности не существует или бесконечен, то числовой ряд называется расходящимся (расходящийся ряд не имеет суммы).

Например, ряд – расходящийся, так как предел последовательности его конечных сумм , , , …, , … бесконечен:

при .

Ряд также расходящийся, так как последовательность его конечных сумм , , , …, … не имеет предела.

Ряд сходящийся, так как предел последовательности его конечных сумм , , , …, равен 0.

Ряд – сходящийся, так как последовательность его конечных сумм , , , …, , … имеет предел, равный 2.

Если отбросить первые членов ряда (1) , то получим ряд:

, (2)

который сходится (расходится), если сходится (расходится) ряд (1). Поэтому при исследовании сходимости ряда можно оставить без внимания несколько начальных членов.

В случае, когда ряд (1) сходится, сумма называется остатком или остаточным членом ряда (1). Таким образом, – первый остаток, – второй остаток и так далее.

Остаток есть погрешность, совершаемая при замене суммы ряда (1) частичной суммой . Сумма ряда и остаток ряда связаны отношением . При остаток ряда стремится к нулю. Если это стремление быстрое, то ряд (1) сходится быстро, иначе – медленно.

Ряд геометрической прогрессии. Ряд

( )

называется рядом геометрической прогрессии.

Исследуем его на сходимость.

Сумма первых членов прогрессии находится по формуле , . Найдём предел этой суммы:

.

Возможны следующие случаи:

1. .

Тогда при . Поэтому , ряд геометрической прогрессии сходится и его сумма равна ;

2. .

Тогда при . Поэтому , ряд геометрической прогрессии расходится;

3. .

Если , то ряд геометрической прогрессии имеет вид . Для него и , ряд расходится.

Если , то ряд геометрической прогрессии имеет вид . Для него при чётном и при нечётном . Значит, не существует, ряд расходится.

Итак, ряд геометрической прогрессии сходится при и расходится при .

► Пример. Показать, что ряд сходится.

Решение. Запишем данный ряд в следующем виде:

Получили ряд геометрической прогрессии, в котором , . Этот ряд сходится, так как

. ◄

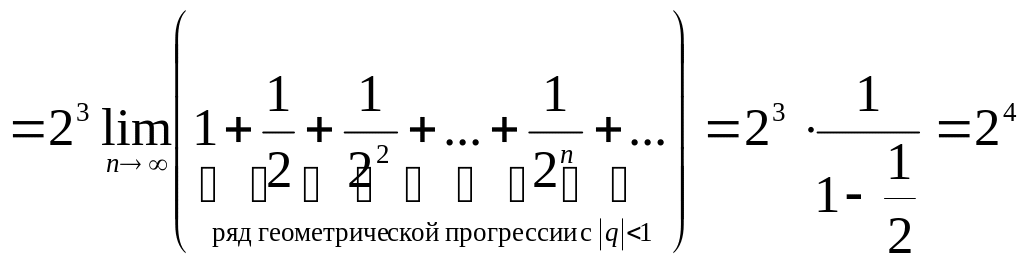Простейшие действия над рядами. Произведением ряда на число называется ряд

.

Суммой (разностью) двух рядов и называется ряд

.

■ Теорема 1.1. Если ряд сходится, то ряд также сходится, причем . Если сходятся ряды и , то сходится ряд , причем . ■

Замечание. Правила действий над рядами не всегда совпадают с правилами действий над конечными суммами. В частности, в конечных суммах можно произвольно менять порядок слагаемых, как угодно группировать члены, сумма от этого не изменится. Слагаемые конечной суммы можно складывать в обратном порядке, для ряда такой возможности нет, так как у него не существует последнего члена.

В ряде не всегда можно группировать члены. Например, ряд является расходящимся. После группировки его членов получаем сходящийся ряд, его сумма равна нулю. При другой группировке членов получаем сходящийся ряд, сумма которого равна единице.

102