5МНК

ЛЕКЦИЯ 5. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК)

При обработке результатов наблюдений можно столкнуться со следующей проблемой: получен ряд значений переменных и , требуется определить характер функциональной зависимости между ними. Формулы, полученные при решении подобных задач, называются эмпирическими. Одним из методов получения эмпирических формул является метод наименьших квадратов. Рассмотрим принцип его действия.

Пусть имеются последовательные значения независимой переменной :

, , …,

и соответствующие им значения зависимой переменной :

, , …, .

Предположим, что, исходя из теоретических соображений, известен вид функциональной зависимости между этими переменными:

, (1)

где , , …, ( ) – неизвестные параметры, которые нужно определить.

Требуется на основании опытных данных определить значения этих параметров так, чтобы заданная функция наилучшим образом описывала изучаемую зависимость (то есть наилучшим образом «вложить» известные пар значений в формулу (1)). Для этого сумма квадратов отклонений эмпирических данных , , от вычисленных по формуле , должна быть наименьшей. Значит, нужно исследовать на минимум функцию:

. (2)

Для определения неизвестных параметров , , …, применим необходимое условие существования экстремума функции нескольких переменных, согласно которому значения параметров находятся из системы уравнений с неизвестными (нормальная система МНК):

(3)

Рассмотрим некоторые частные случаи предполагаемой функциональной зависимости.

1. Если переменные и связаны линейной зависимостью

, (4)

то частные производные функции (2)

по параметрам , имеют вид:

,

.

Приравняем их нулю и преобразуем. Получаем нормальную систему МНК, из которой находим параметры , :

(5)

Для определения коэффициентов системы (5) удобно составлять вспомогательную таблицу (см. таб. 1). В последней строке запишем суммы элементов каждого столбца, которые и являются коэффициентами системы (5).

Таблица 1

1
2
…	…	…	…	…

2. Если переменные связаны зависимостью вида

, (6)

то частные производные функции (2)

по параметрам , , имеют вид:

,

,

.

Приравняем их нулю и преобразуем. Получаем нормальную систему МНК для нахождения , , :

(7)

3. Если переменные связаны зависимостью вида

, (8)

то частные производные функции

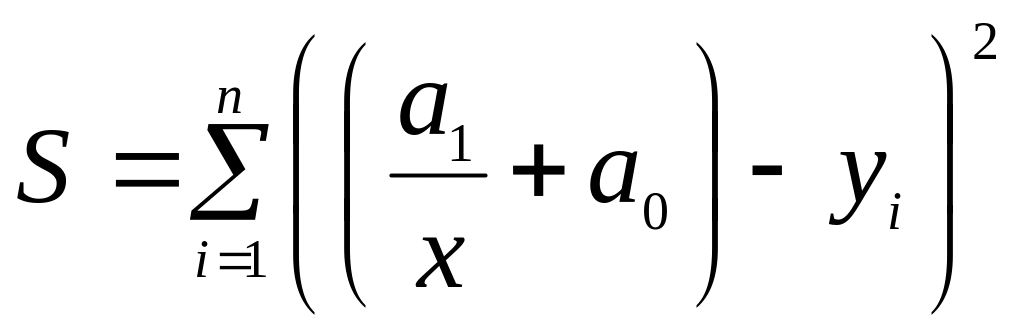
по параметрам , имеют вид:

,

.

Приравняем их нулю и преобразуем. Получаем систему:

(9)

► Пример. Рост производства химволокна по годам представлен в таблице 2.

Год х	1-й	2-й	3-й	4-й
Количество химволокна y тыс.т.	623	676	746	829

Таблица 2

Предполагая, что между переменными и существует линейная зависимость, найти эмпирическую формулу вида .

Решение. Для составления нормальной системы (5) необходимые результаты вычислений занесем в таблицу 3.

Таблица 3

1	1	623	623	1
2	2	676	1352	4
3	3	746	2238	9
4	4	829	3316	16
	10	2874	7529	30

Подставив найденные значения сумм, получим нормальную систему вида:

Решая эту систему, получим , . Искомая эмпирическая формула имеет вид: .

Изобразим в системе координат эмпирические точки и график полученной линейной зависимости. ◄

4