3Производная по направлению вектора

ЛЕКЦИЯ 3. ПРОИЗВОДНАЯ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ ПО НАПРАВЛЕНИЮ ВЕКТОРА

Производная функции двух переменных по направлению вектора. Рассмотрим в области упорядоченных пар чисел функцию и точку .

Проведем из точки вектор , направляющие косинусы которого есть и (рис. 1). На векторе , на расстоянии от его начала, рассмотрим точку . Тогда

.

Предположим, что функция непрерывна и имеет непрерывные производные по своим аргументам в области . Полное приращение функции в точке можно представить в виде:

,

г де , при , (то есть при ).

Разделим все члены равенства на величину :

.

Очевидно, что

, .

Тогда

.

Определение 3.1. Предел отношения при называется производной функции в точке по направлению вектора и обозначается , то есть

.

Таким образом, вычислив частные производные, легко найти производную по любому направлению . Сами частные производные есть частный случай производной по направлению. Например, производная функции в направлении оси , то есть при и , равна:

.

► Пример. Дана функция . Найти производную в точке в направлении вектора .

Решение. Найдем направляющие косинусы вектора :

, .

Найдем частные производные данной функции в точке :

, ;

, .

Получаем:

. ◄

Градиент

Определение 3.2. Градиентом функции в точке называется вектор, координатами которого являются значения частных производных этой функции в данной точке:

или .

Градиент функции в точке характеризует направление и величину самого быстрого роста этой функции в указанной точке, то есть:

1. производная функции в точке в направлении градиента этой функции в указанной точке, имеет максимальное значение по сравнению с производной в точке по любому другому направлению;

2. значение производной функции в направлении градиента этой функции в точке равно .

► Пример. Найти направление наискорейшего роста функции из предыдущего примера и указать значение производной этой функции в этом направлении в точке .

Решение. Самый быстрый рост функции в точке происходит в направлении градиента этой функции в данной точке. Координатами градиента функции в точке являются значения частных производных данной функции в данной точке, то есть

.

Угловой коэффициент градиента равен

.

Следовательно, искомое направление составляет угол с осью .

Производная по направлению, составляющему угол с осью , в точке равно длине , то есть

. ◄

Существует четкая связь между линиями уровня функции и направлением градиента этой функции.

■ Теорема 3.1. Пусть задана дифференцируемая функция и величина градиента этой функции, отличная от нуля, в точке . Тогда градиент в точке перпендикулярен касательной к линии уровня, проходящей через эту точку. ■

► Пример. Для функции построить линию уровня, проходящую через точку и найти градиент в данной точке.

Решение. Уровень в исследуемой точке равен . Линия уровня определяется формулой или . Таким образом, линией уровня является гипербола.

Для отыскания градиента найдем частные производные функции в исследуемой точке:

,

.

Отсюда следует выражение для градиента функции в исследуемой точке:

.

Из полученной формулы видно, что градиент в исследуемой точке находится в первой четверти и проходит под углом 45° к осям и .

Модуль градиента равен:

. ◄

Дифференцирование сложных функций. Пусть дана функция , но переменные , , зависят, например, от переменных и :

, , , .

Тогда – сложная функция и .

Например, функция , где , .

Полный дифференциал сложной функции переменных и равен сумме частных дифференциалов переменных , , :

,

где

, , .

Следовательно,

.

Таким образом, частная производная сложной функции по одной из независимых переменных равна сумме произведений её частных производных по промежуточным аргументам на частные производные этих аргументов по данной независимой переменной.

Если все промежуточные аргументы являются функциями одной независимой переменной (например, , где , ), то является сложной функцией , а её производная называется полной. Полная производная находится по формуле

.

► Пример. Найти функции , где , .

Решение. Функция зависит от двух промежуточных аргументов и . Поэтому

.

Имеем

. ◄

Неявная функция и её дифференцирование. Пусть функция имеет вид

.

При подстановке в уравнение получим тождество по :

.

В этом случае функция называется заданной неявно в виде уравнения .

Например, , , .

Для вычисления производной надо зафиксировать и дифференцировать обе части уравнения , учитывая, что зависит от . По правилу дифференцирования сложной функции получим

или ,

откуда

.

Аналогично получим

.

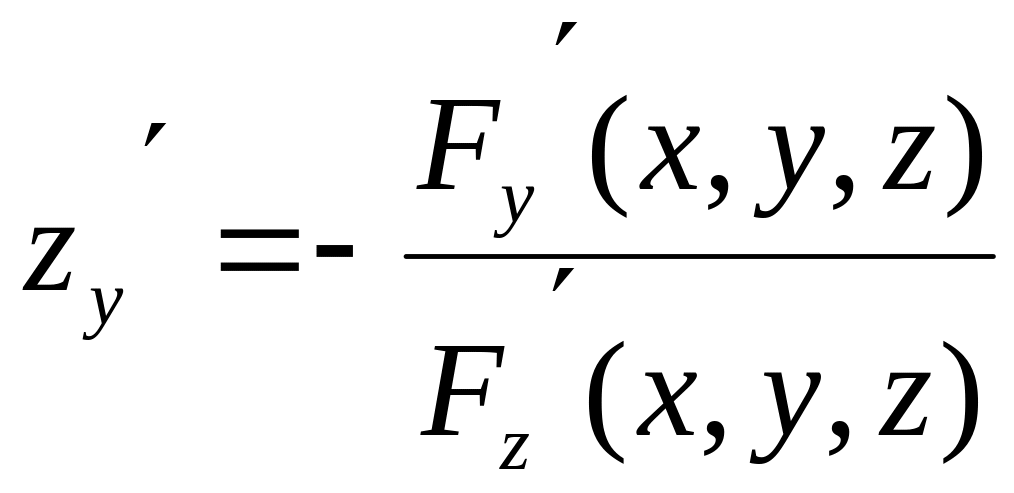Естественным требованием является следующее

.

Оно является условием существования неявной функции .

► Пример. Найти частные производные первого и второго порядков функции , .

Решение. Продифференцируем данное уравнение по и по :

, . (*)

Отсюда

, .

Продифференцируем первое из соотношений (*) по , а второе – по :

, .

Отсюда с учётом и имеем:

, .

Дифференцируем первое из уравнений (*) по (или второе – по ):

.

Отсюда

. ◄

6