2Частные производные, полный дифференциал

ЛЕКЦИЯ 2. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

Частные производные функции двух переменных. Зафиксируем значение одной из переменных функции , тогда становится функцией этой одной переменной и по ней можно брать производную или дифференциал (если они существуют). Такие производные и дифференциалы называются частными.

Определение 2.1. Частной производной первого порядка функции по переменной ( ) в точке называется предел отношения приращения функции по ( ) к приращению самой переменной при стремлении последнего к нулю:

( ).

Таким образом, частной производной по аргументу функции является производная этой функции по при постоянном , а частной производной по аргументу – производная этой функции при постоянном .

Обозначения: , , , .

Частная производная функции по переменной выражает скорость изменения функции в данном направлении ( ), или скорость изменения функции одной переменной .

Определение 2.2. Частными производными второго порядка функции называются частные производные от её частных производных первого порядка.

Они обозначаются: , , , , , , , .

Частные производные , называются смешанными частными производными второго порядка.

Отметим, что смешанные частные производные второго порядка равны между собой. Это замечание справедливо для смешанных производных любого порядка.

Таким образом, частная производная -го порядка функции есть первая частная производная от её частной производной -го порядка.

Аналогично определяются и вычисляются частные производные второго и высших порядков от функции трёх и большего числа переменных.

► Пример. Найти частные производные второго порядка функций:

а) ;

б) ;

в) в точке .

Решение. а) Найдем частные производные первого порядка:

; .

Найдем частные производные второго порядка:

; ; ; .

Действительно,

. ◄

Геометрический смысл частных производных функции двух переменных. Графиком функции является некоторая поверхность (рис. 1). Уравнение задаёт плоскость, параллельную координатной плоскости . Линию пересечения функции и плоскости описывает функция или (функция одной переменной). Её производная в точке имеет вид:

.

Геометрический смысл этой производной:

,

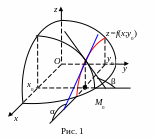где – угол между осью и касательной к кривой в точке .

Аналогично, , где – угол между осью и касательной к кривой в точке .

Полное приращение и полный дифференциал функции двух переменных

Определение 2.3. Полным приращением функции двух переменных называется изменение функции при заданных приращениях всех переменных.

В частности, полным приращением функции в точке является разность

.

Представим эту разность следующим образом:

.

Рассмотрим частную производную функции в точке по переменной : . По определению 2.1 частных производных

.

Тогда

,

где при .

Преобразуем последнее равенство:

,

где при , при .

Далее

,

где при , .

В итоге получаем

,

где при , .

Аналогично

,

где при , .

Запишем полное приращение функции в точке с учетом проведённых преобразований:

,

где , при , .

Сумма первых двух слагаемых в последнем равенстве представляет собой главную часть приращения функции.

Определение 2.4. Полным дифференциалом в точке функции называется главная линейная относительно и часть полного приращения функции в этой точке:

.

Дифференциалы независимых переменных равны их приращениям:

, ,

поэтому полный дифференциал функции находится по формуле:

,

где – частный дифференциал функции по переменной , – частный дифференциал функции по переменной .

Аналогично определяется полный дифференциал функции любого числа переменных. Функция, имеющая полный дифференциал в данной точке, называется дифференцируемой в этой точке. Таким образом, если в данной точке и некоторой её окрестности частные производные функции непрерывны, то функция дифференцируема в этой точке (обратное также верно).

Полным дифференциалом второго порядка функции называется полный дифференциал её полного дифференциала:

.

Таким образом, получаем

.

► Пример. Найти полные дифференциалы первого и второго порядков функции .

Решение. Находим частные производные первого порядка:

, .

Полный дифференциал первого порядка данной функции имеет вид:

.

Находим частные производные второго порядка:

,

,

.

Полный дифференциал второго порядка данной функции имеет вид:

.◄

При достаточно малых и для дифференцируемой в точке функции верно приближенное равенство

или

,

откуда

Последняя формула для приближенных вычислений значения функции в точке .

► Пример. Найти изменение объема конуса с высотой 30 см и радиусом основания 10 см при увеличении этих измерений на 3 мм и на 1 мм соответственно.

Решение. Объем конуса есть функция двух переменных и . Для решения задачи используем приближенное равенство:

или .

Найдем значения частных производных и в точке :

, ;

, .

Так как см и см, то

(см³). ◄

5