Файловый архив студентов. Файловый архив студентов.
1264 вуза, 4634 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Полоцкий Государственный Университет
Предмет:
Физика
Файл:
С.А.Вабищевич, В.А.Груздев, Г.А.Дубченок, В.Г.Залесский, Г.М.Макаренко Учебно-методический комплекс по общей физике. Часть 2.pdf
Скачиваний:
12
Добавлен:
18.02.2023
Размер:
4.32 Mб
Скачать
☆
►Содержание►

3.4. Примеры решения задач

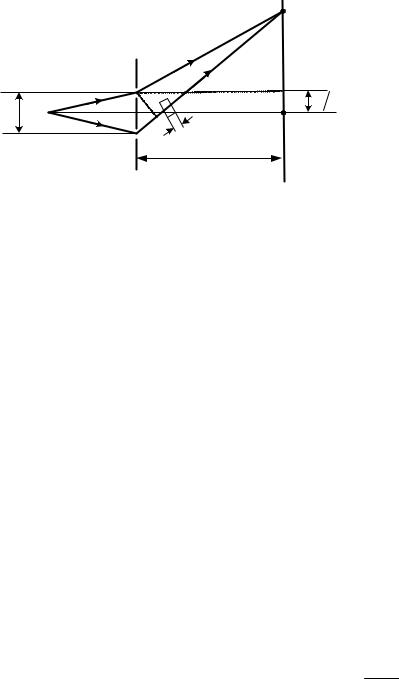
Пример 1. В опыте Юнга на пути одного из интерферирующих лучей помещалась тонкая стеклянная пластинка C , вследствие чего центральная световая полоса смещалась в положение, первоначально занятое пятой светлой полосой (не считая центральной). Луч падает на пластинку перпендикулярно. Показатель преломления пластинки 1,5.

Длина световой

волны

0 600 нм. Какова

толщина

пластинки h?

 

 

A

 

(Уровень 4).

 

 

 

 

 

 

Решение.

Рассмотрим

 

 

1

 

 

 

l1

 

схему опыта Юнга (см.

рис.

 

2

 

 

 

3.15). В некоторой точке А, где

S

l2

 

 

 

складываются

колебания

1

C

 

d 2

d S*

B

световых лучей 1 и 2, будет

S2

h

l

 

наблюдаться световое пятно (m-

 

ный

максимум),

если

П

 

Э

 

оптическая разность хода лучей

 

 

 

 

равна m 0 .

 

 

 

Рис. 3.15

 

Луч 1 проходит через воздух –

 

 

 

 

его

оптическая

длина

пути

равна геометрической длине пути l1. Луч 2 проходит часть пути в стеклянной пластинке толщиной h. Его оптическая длина пути будет равнаl2 h hn. Оптическая разность хода лучей 1 и 2 в этом случае равна

/ l

h hn l .

 

 

 

 

 

(1)

 

2

 

 

1

 

 

 

 

 

 

Если стеклянную пластинку С убрать, то оптическая разность хода

выбранных лучей

l2 l1 .

 

 

 

 

 

 

(2)

 

 

 

 

 

 

 

По условию задачи интерференционная картина при наличии

пластинки C смещается на пять полос, то есть, если

 

 

 

 

 

 

то

l2 l1 m 0 ,

 

 

 

 

 

(3)

 

 

 

 

 

 

 

 

 

 

/ l

h hn l

m 5

0

.

 

 

 

(4)

2

 

1

 

 

 

 

 

 

 

Вычитая из (4) выражение (3), получим

 

 

 

 

 

 

/ l h hn l l l

m 5

0

m

0

,

2

1

2

1

 

 

 

 

 

или

n 1 h 5 0 , и h 5 0 . n 1

276

Толщинапластинкиh равна6микрометрам.Этазадачаиллюстрирует один

извозможныхспособовопределения толщинысветопрозрачныхматериалов.

Ответ:h =6кмк.

 

 

 

 

 

 

 

Пример 2. Для наблюдения колец Ньютона плосковыпуклая линза

положена выпуклой стороной на стеклянную пластинку. Найти радиус

кривизны линзы, если радиусы четвертого и одиннадцатого темных колец,

наблюдаемых в отраженном свете, равны соответственно 0,15 мм и 6,7 мм.

Длина световой волны 0 = 700 нм (Уровень 4).

 

 

 

 

 

 

 

Решение.

Рассмотрим

схему

 

 

 

наблюдения

 

интерференционной

 

 

O

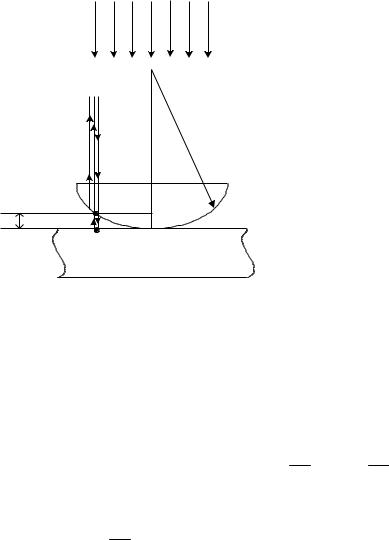
картины (см. рис. 3.16). Световые лучи

 

 

падают

на

плосковыпуклую

линзу

 

 

перпендикулярно

поверхности

MN.

 

211

 

 

 

 

Наблюдая интерференционную картину

 

 

R

в отраженном свете, можно видеть

 

 

 

набор

светлых

и

темных

 

 

 

концентрических колец (в проходящем

d

A

D

свете их также возможно наблюдать).

2

C

Разделение светового пучка (луч 1) на

 

A1

два происходит за счет того, что часть

 

 

 

 

 

 

 

 

 

 

 

 

 

светового потока (луч 1 ) отражается от

 

Рис. 3.16

границы линза – воздух (точка А на

 

рис3.16), а вторая часть пучка проходит

через воздушный интервал АА1 и отражается от границы воздух–стекло (точка

А1 – см. рис. 3.16). Так как радиус кривизны линз в таких схемах порядка

нескольких

метров, а зазор

между

линзой

и

пластинкой

достаточно мал

(несколько миллиметров), то лучи, отраженные от точек А и А1 пойдут по одной

прямой.Оптическаяразностьходаэтихлучей

 

 

 

 

 

 

 

2АА 0 2d 0 ,

 

 

(1)

 

 

 

1

2

 

2

 

 

 

 

 

 

 

 

 

 

 

где d – величина зазора АА1 (см. рис), и учитывается дополнительная

разность хода 0 , так как при отражении от более плотной среды (в точке

 

 

2

 

 

 

 

 

 

 

A1) один луч теряет половину длины волны.

 

 

 

 

 

Предположим, что при наложении лучей, отраженных от точек А и

А1, наблюдается m-ный минимум. Тогда расстояние AD (см. рис. 3.16) или

А1С есть радиус m-го темного кольца rm. Из треугольника AOD, учитывая,

что АO = R – радиус кривизны линзы, получим

 

 

 

 

277

r2

R2 R d 2 2Rd

d2

.

 

 

 

m

 

 

 

 

4

 

 

Так как d R

 

 

 

 

 

 

(таковы требования

к этой

схеме получения

интерференционной картины), величиной

 

d

2

 

можно

пренебречь, как

4

 

очень малой. Учитывая это, получим

 

 

 

 

 

 

 

 

 

 

 

 

r2

2Rd , и d

rm2

.

 

 

 

(2)

 

 

 

 

 

 

m

 

2R

 

 

 

 

 

 

 

 

 

 

 

 

 

Подставляя формулу (2) в (1), получим оптическую разность хода интерферирующих лучей

rm2 0 .

R 2

Если эта оптическая разность хода равна нечетному числу полуволн, получим условие m-го минимума

 

r2

 

0

2m 1

 

0

 

r2

 

m

 

 

 

, или

m

m 0 .

 

2

2

 

 

R

 

 

R

Тогдадля четвертого иодиннадцатого темныхколецполучим условия:

 

r2

 

 

4

 

4 0 ,

(3)

 

 

 

 

R

 

r2

 

 

11

11 0 .

(4)

 

 

 

R

 

Вычитая из уравнения (4) выражение (3), получим

r2

r

2

 

 

r2

r2

 

11

4

7 0 или

R

11

4

.

(5)

 

R

 

 

 

 

 

 

 

7 0

 

Подставляя в формулу (5) данные в системе СИ, получим

 

 

3

 

2

3

 

2

м

2

 

 

6,7 10

 

0,15 10

 

 

 

 

R

 

 

 

 

 

 

 

 

 

9,1 м.

 

7 7 10 7 м

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: R = 9,1 м.

 

 

 

 

 

 

 

 

 

Пример 3. На мыльную пленку падает белый свет под углом i = 450 к поверхности пленки. При какой наименьшей толщине пленки отраженные лучи будут окрашены в желтый цвет ( 0 = 600 нм)? Показатель преломления мыльной водыn = 1,33 (Уровень 3).

278

Рис. 3.17

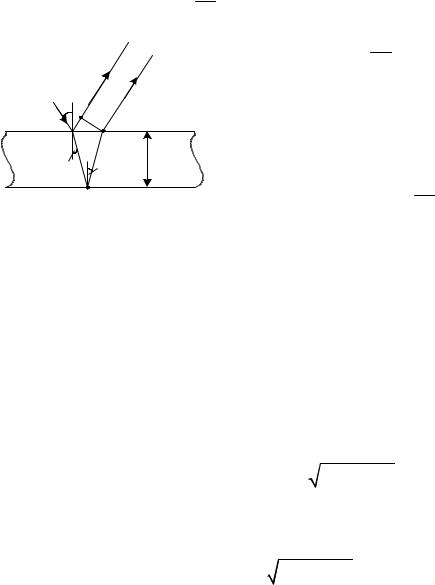
Решение. По условию отраженные лучи окрашены в желтый цвет. Это означает, что максимум отражения наблюдается в желтой части спектра. Максимум отражения наблюдается, когда световые волны, отраженные от обеих поверхностей пластинки, усиливают друг друга. Для этого оптическая разность хода пучков 1 и 2 должна быть равна целому числу m длин волн

 

 

 

 

0 n(AC BC) AD m 0 .

 

 

 

 

 

2

 

 

 

 

 

 

 

 

Слагаемое

0

учитывает, что

при

 

 

 

 

 

2

 

 

 

 

1

 

отражении пучка 1 от оптически более плотной

 

i D

 

2

 

 

среды фаза колебаний электромагнитного поля

 

1

 

 

 

A

 

изменяется

на

противоположную,

т.е.

n

B

 

r

r

h

возникает такое же изменение фазы, как при

 

 

С

 

прохождении

пути

0 . Множитель

n

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

учитывает уменьшение скорости света в среде

– на пути s в среде возникает такое же изменение фазы ,какнапути ns ввакууме

 

 

 

 

2 ns

 

 

2

.

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

Используя соотношения

 

 

 

 

 

 

 

 

 

 

 

 

 

 

AC BC

 

 

 

h

 

;

 

 

 

 

 

AD 2hsini tgr ,

 

cosr

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а также, применяя закон преломления, получаем

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n2 sin2 i ,

m

 

 

 

 

0

2h

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

откуда

 

 

 

 

 

 

 

m 1/ 2 0

 

 

 

 

 

h

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

n2 sin2 i

 

 

 

 

 

 

 

 

 

 

 

 

При m = 1 минимальная толщина пленки hmin = 0,13 10–6 м.

Ответ: hmin = 0,13 10–6 м.

Пример 5. На поверхность стеклянного объектива (n1 = 1,5) нанесена тонкая пленка, показатель преломления которой n2 = 1,2 (просветляющая пленка). При какой наименьшей толщине d этой пленки произойдет

279

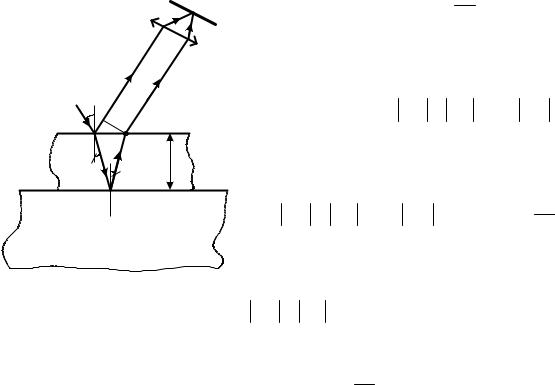
максимальное ослабление отраженного света в средней части видимого спектра ( 0 552 нм)? (Уровень 3).

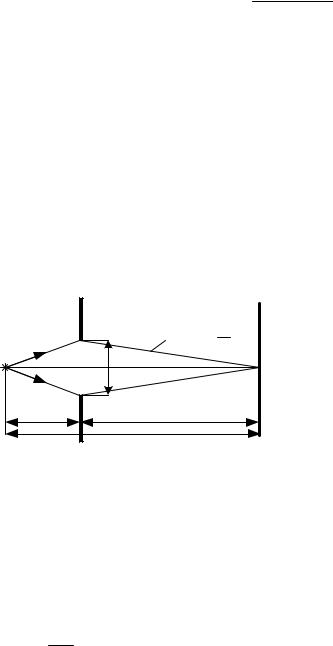
Решение. Из световой волны, падающей на пленку, выделим узкий пучок SB. В точках В и C падающий пучок частично отражается и частично преломляется. Отраженные пучки света 1 и 2 падают на собирающую линзу, пересекаются в ее фокусе и интерферируют между собой. Т.к. показатель преломления воздуха (n = 1) меньше показателя преломления вещества пленки n2 , который, в свою очередь, меньше показателя преломления

стекла n1 , то в обоих случаях (в точках B и C ) отражение происходит от среды оптически более плотной, чем та среда, в которой идет падающая волна. Поэтому фаза колебания пучка света 1 при отражении в точке B изменяется на и точно так же на изменяется фаза колебаний пучка света 2 при отражении в точке С. Следовательно, результат интерференции этих пучков света при пересечении в фокусе линзы будет такой же, как если бы никакого изменения фазы колебаний ни у того ни у другого пучка не было. Условие максимального ослабления света при интерференции в тонких пленках состоит в том, что оптическая разность хода интерферирующих волн должна быть равна нечетному числу полуволн

 

 

 

 

(2m 1)

 

 

0

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

Э

 

2

 

 

 

 

 

 

L

 

 

 

 

 

 

 

 

 

Как видно из рис. 3.18, оптическая

 

 

1

2

разность хода

 

 

 

 

 

 

S* i

D A

l2n2 l1n BC CA n2 AD n .

 

n

1

 

 

 

 

 

 

 

 

B

2

d

Следовательно, условие

минимума

 

2

интенсивности света приметвид

 

 

 

r

r

 

 

 

 

 

 

n n

С

 

BC CA n2 AD n (2m

0

 

1

2

 

 

1)

.

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

Если угол падения i будет

 

Рис.3.18

 

уменьшаться, стремясь к нулю, то АD 0 и

 

 

BC CA 2d , где d – толщина пленки. В

 

 

 

 

пределе при i = 0 получим

 

 

 

 

 

 

 

2dn2 (2m 1) 0 ,

2

откуда искомая толщина пленки

280

d (2m 1) 0 . 4n2

Минимальное значение dmin соответствует значению m = 0.

Подставляя числовые данные, получим dmin = 115 10–9 м.

Ответ: dmin = 115 10–9 м.

Пример 5. Точечныйисточниксвета,излучающий свет длиной

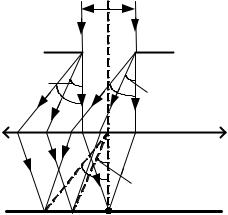
= 550 нм, освещает экран, расположенный на расстоянии l = 11 м от источника. Между источником и экраном на расстоянии b = 5 м помещена ширма (преграда П) с круглым отверстием диаметром d = 4,2 мм. В каком случае (с ширмой или без нее) интенсивность в центре экрана будет больше? (Уровень 3).

 

 

 

Решение.

Рассмотрим

 

 

b m

дифракцию

Френеля

на

круглом

 

 

2

отверстии. Оценим интенсивность в

S

 

 

центре экрана (точка Р – рис. 3.19)

 

 

в случае, когда ширма П убрана, то

a

 

b

 

есть волновая поверхность световой

 

П

Э

волны

полностью

 

открыта.

 

 

Рассчитаем

результирующую

 

 

 

 

Рис. 3.19

 

амплитуду колебаний в точке Р.

 

 

 

Учитывая

монотонное

убывание

амплитуды с увеличением номера зоны m, можно считать, что результирующая

амплитуда колебаний А в центре экрана равна согласно (26)

 

 

A

A1

 

Am

 

A1

(1)

 

2

 

2

 

2

 

(так как Am 0 для бесконечно большого числа m).

2

В этом случае интенсивность в центре экрана I будет равна

I ~ A2

A12

.

(2)

 

4

Если на пути световой волны поставить ширму с круглым отверстием, то число зон Френеля, открытых отверстием, можно рассчитать по формуле (27). По условию b = 5 м, а а = l – b = 6 м. Подставив данные задачи в формулу (27), получим

281

m

4,2

2 10 6 м2

11 м

 

 

 

2,94 3.

4 5,5 10 7 м 5

 

 

м 6 м

Число зон Френеля, открытых отверстием, равно трем. Пользуясь формулой (26), оценим амплитуду А и интенсивность I в центре экрана

A

A1

 

A3

;

 

(3)

 

 

 

 

 

2

 

2

 

2

 

I ~ A2

 

 

A

 

 

A

 

 

1

 

3

.

(4)

2

 

 

 

 

2

 

 

Сравнивая формулы (4) и (2), делаем вывод, что интенсивность в центре экрана будет больше в случае, когда на пути световой волны стоит ширма с круглым отверстием.

Ответ: Интенсивность в центре экрана будет больше в случае, когда на пути световой волны стоит ширма с круглым отверстием.

 

a

 

1

 

1

2

2

 

 

O

L

2 1

A2 A1 A

Э

 

Рис. 3.20

для границ видимого спектра (от

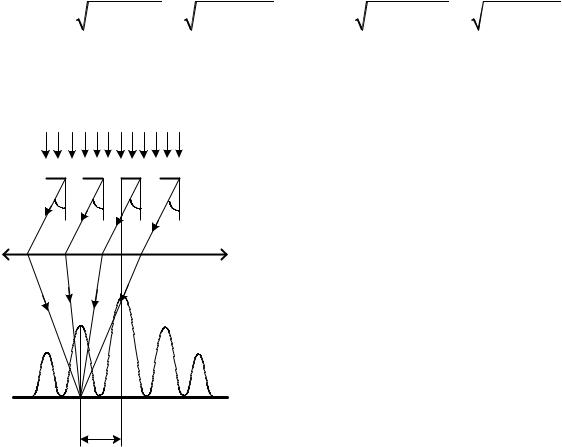
Пример 6. На щель шириной а = 30 мкм нормально падает белый свет. Спектр проецируется на экран с линзой с фокусным расстоянием f = 195 см. Определить ширину спектра десятого порядка, если границы видимого спектра лежат от 400 нм до 780 нм (Уровень 4).

Решение. Обозначим углы дифракции для минимальной и максимальной длин волн в спектре десятого порядка, соответственно, 1 и

2 (см. рис. 3.20).

Условие минимума m-го порядка1 до 2 ) можно записать

asin 1

m 1,

(1)

asin 2

m 2 .

(2)

Так как экран стоит в фокальной плоскости линзы (расстояние ОА = f), (см. рис. 3.20), то лучи с длиной волны 1 , дифрагирующие под углом 1,

соберутся в точке А1, а лучи с длиной волны 2 в точке А2.

Расстояния от центра экрана А до соответствующих точек А1 и А2 можно рассчитать как

282

 

 

AA1 f tg 1 ,

(3)

 

 

AA2 f tg 2 .

(4)

Если углы 1 и

2

малы, то tg можно заменить на

sin . Тогда

искомое расстояние А1А2 (ширина спектра m-го порядка), используя формулы (1) – (4), получится равным

A A

f tg

2

tg f sin

2

sin

f

m

 

 

2

 

.

(5)

 

1

2

 

 

 

1

1

 

a

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Подставляя данные задачи в формулу (5), получим

 

 

 

 

 

 

A A

1,95

м 10 3,8 10 7 м

25 10 2 м 25 см.

 

 

 

 

 

 

 

 

 

1

2

 

 

3 10 5 м

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для сравнения можно подсчитать ширину спектра первого порядка, она будет в десять раз меньше, то есть 2,5 см.

Задачу можно решить точнее, рассчитав tg 1 и tg 2 по формулам

tg

 

sin 1

 

 

 

m 1

 

и tg

2

 

 

sin 21

 

 

 

m 2

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

1 sin

2

 

 

 

a2 m2 2

 

 

 

1 sin2

 

 

 

a2 m2 2

 

 

 

 

 

 

 

 

 

21

 

 

 

 

 

 

1

 

 

 

1

 

 

 

 

 

 

 

 

2

 

В этом случае ширина спектра получается равной 26 см (погрешность порядка 4 % для приближенного расчета величины А1А2).

Ответ: А1А2 = 25 см.

 

 

 

ДР

 

 

 

 

 

 

 

L

 

 

 

Э

m 2 m 1m 0 m 1 m 2

 

l

 

 

 

Рис. 3.21

 

Пример 7. На дифракционную решетку Д нормально падает монохроматический свет с длиной волны 0,65 мкм. На экране Э, расположенном параллельно решетке и отстоящем от нее на расстояние 0,5 м, наблюдается дифракционная картина (см. рис. 3.21). Расстояние между дифракционными максимумами первого порядка равно 10 см. Определить постоянную дифракционной решетки и общее число главных максимумов, получаемых с помощью этой решетки (Уровень 3).

Решение. Запишем условие главных максимумовдифракционнойрешетки

d sin m ,

(1)

283

где d – постоянная дифракционной решетки, – угол отклонения лучей от нормального направления распространения света; m – порядок главного дифракционного максимума; – длина волны падающего на решетку монохроматического света.

По условию задачи m = 1. Учитывая, что l2 L

sin tg l 2L .

(2)

Подставляя (2) в (1), получим

dl

или d

2 L

.

(3)

2L

 

 

l

 

Подставляя в (3) числовые значения величин, находим

d 2 0,65 10 6 м 0,5 м 6,5 10 6 м 0,65 мкм. 0,1 м

Для определения общего числа главных максимумов, даваемых дифракционной решеткой, исходим из условия, что максимальный угол отклонения лучей от нормального направления распространения не может превышать 90 , т.е. sin90 1, тогда формула (1) примет вид mmax d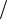 . Производим вычисления mmax 6,5 10 6 м/0,65 10 6м 10.

Общее число максимумов равно n 2mmax 1, т.е. влево и вправо от центрального максимума будут наблюдаться по mmax максимумов:

n 2 10 1 21.

Ответ: n 21.

Пример 8. При каком минимальном числе штрихов дифракционной решетки с периодом d = 2,9 мкм можно разрешить компоненты дублета желтой линии натрия ( 1 = 5890 А и 2 = 5896 А)? (Уровень 3).

Решение. Число штрихов N решетки связано с ее разрешающей

силой R и порядком спектра m , причем N R / m .

Минимальному

значению Nмин соответствует минимальное значение Rмин и максимальное

число m , т.е.

 

Nmin Rmin / mmax .

(1)

Минимальная разрешающая сила решетки Rмин, необходимая для разрешения дублета (двух составляющих) желтой линии натрия, выражается через две величины 1 , 2 по формуле

284

Соседние файлы в предмете Физика
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности