Добавил:

oih07968 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

С.А.Вабищевич, В.А.Груздев, Г.А.Дубченок, В.Г.Залесский, Г.М.Макаренко Учебно-методический комплекс по общей физике. Часть 2.pdf

Скачиваний:

Добавлен:

18.02.2023

Размер:

4.32 Mб

Скачать

☆

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2526 / 3526 27 28 29 30 31 32 33 34 35 > Следующая >>>

2.4. Примеры решения задач

Построение изображения в тонких линзах

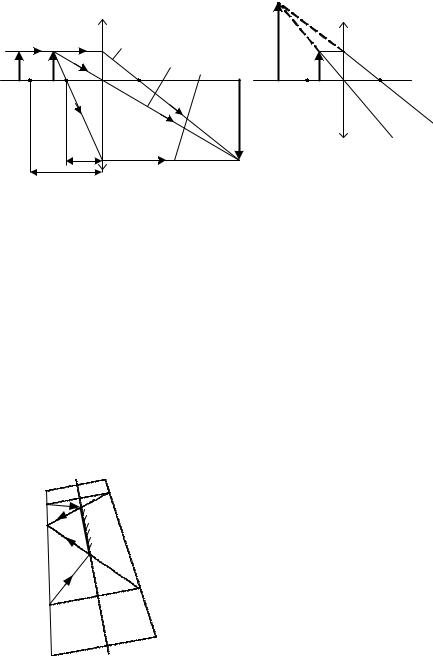
Изображение любой точки предмета в линзе находится в точке

пересечения двух лучей (или их продолжений), вышедших из этой точки

предмета и прошедших через линзу. Обычно для построения изображения

используются два из трех лучей (рис. 2.17 а)): луч 1, проходящий без

преломления через оптический центр линзы; луч, падающий параллельно

главной оптической оси; после преломления в линзе этот луч (или его

продолжение) проходит через задний (относительно предмета) главный

фокус;

луч (или

его

продолжение),

который

проходит через

передний

главный

фокус

после

преломления идет

параллельно

главной

оптической оси.

Ход

луча

одинаков

во

всех

а)

б)

двух

случаях,

Рис. 2.17

луч

идет

или

под

большим

углом к оси (если расстояние от центра линзы до предмета меньше 2f, но

больше f), или под меньшим (если расстояние больше 2f). Изображение

получается действительное, перевернутое и либо уменьшенное, либо

увеличенное.

Если предмет (стрелка АВ на рис. 2.17 б)) расположен между

фокусом и линзой, то лучи BDF и ВО не пересекаются. Поэтому нужно

строить

пересечение

их

продолжений

(см.

пунктир на

рис.

2.17,

б).

Изображение

мнимое (пересекаются не лучи,

а их продолжения),

A B

увеличенное, прямое.

Пример

Человек

смотрится

зеркало,

висящее на

стене

небольшим

наклоном. Постройте изображение человека

в зеркале. Какую часть своего тела будет

видеть

человек?

При

построении

можно

изобразить человека

в виде

отрезка

АВ,

Рис. 2.18

238

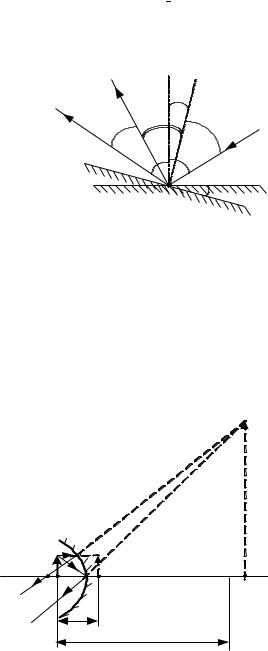
расположив глаз в точке С. (Уровень 2).

Решение. Построим (рис. 2.18) изображение крайних точек человека

А и В.Для этого на плоскость зеркала опускаем перпендикуляры AD и ВЕ и

продолжаем их за зеркало на расстояния, равные соответственно А1D =AD

и B1E=BE.

A1B1 - мнимое изображение человека АВ. Человек увидит только ту часть тела, лучи от которой после отражения попадут в глаз C, т.е. K1L1=KL.

Ответ: K1L1=KL.

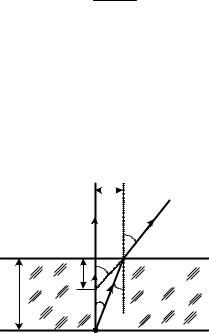
Пример 2. На сколько градусов отклонится отраженный от зеркала

луч, если зеркало повернуть на 15°? (Уровень 2).

Решение: Пусть АО – падающий луч, MN – плоское зеркало. Угол АОС = α

						– угол падения луча, угол СОВ = γ –
	B	C		C		угол отражения. По закону отражения
B		1				γ = α. Следовательно, АОВ = 2α.
				1		γ = α. Следовательно, АОВ = 2α.
					A	Повернем зеркало вокруг точки О
					A	Повернем зеркало вокруг точки О
	N					на угол φ. M'N' – новое положение
	N				M	на угол φ. M'N' – новое положение
	N		O		M	зеркала. ОС'	–	перпендикуляр к
						зеркалу. Углы С'ОС и МОМ' – углы с
					M

						соответственно	перпендикулярными
		Рис. 2.19				соответственно	перпендикулярными
		Рис. 2.19				сторонами. Следовательно, C'OC =
						сторонами. Следовательно, C'OC =
φ. После поворота зеркала АОС' = α1– угол падения,								C'OB' = γ1– угол

отражения, α1 = γ1. Из рисунка видно, что α1 = α - φ. Следовательно,

АОВ' = 2α1 = 2(α - φ). Искомый угол β = В'OB = 2α - 2α1 = 2α - 2(α - φ)

= 2φ; β = 30°.

		B1	Ответ: β = 30°.
		B1
			Пример 3. Чему равен радиус
			вогнутого зеркала, находящегося на
		H	расстоянии 2,0 м от предмета, если его
B	B2		прямое	изображение		в	полтора		раза
B	B2		больше,	чем	в	плоском		зеркале,
F	h		больше,	чем	в	плоском		зеркале,
A	A2	A	находящемся на		том	же	расстоянии от
		1	находящемся на		том	же	расстоянии от
2d	d f
	Рис. 2.20		239

Рис. 2.21

предмета? (Уровень 3).

Решение. Так как изображение, даваемое вогнутым зеркалом, прямое и увеличенное, то предмет АВ находится между фокусом и полюсом зеркала. Запишем формулу сферического зеркала:

1	1	1	2	(1)
		F	R
d	f

На рисунке A1В1 – изображение предмета в сферическом зеркале, А2В2 – в плоском зеркале.

Линейное увеличение сферического зеркала

Г	H	f	(2)

1	h	d

Размеры изображения в плоском зеркале всегда равны размерам предмета,

т.е. Г2= 1. Следовательно,	Г1	= Г1 = 1,5.
	Г2

Тогда f = Г1d.

Подставив значение f в формулу сферического зеркала , получим

1	1	2	.
	Г1d
d		R

Откуда R = 2Г1d = 12 м.

Г1 1

Ответ: R = 12 м.

Пример 4. На нижнюю грань плоскопараллельной стеклянной пластинки ( nc 1,5) нанесена царапина. Наблюдатель, глядя сверху, видит царапину на расстоянии 4 см от верхней грани пластинки. Какова толщина

	пластинки? (Уровень 4).
d	Решение: Пусть царапина находится в точке
	А	нижней	поверхности	стеклянной

пластинки. Построим изображение точки А,

	C	D	которое видит	наблюдатель.	Для этого
	h1		рассмотрим два луча: АС – луч, падающий
h	B		рассмотрим два луча: АС – луч, падающий
h	B		перпендикулярно	на верхнюю	поверхность
	A		перпендикулярно	на верхнюю	поверхность
	A

пластинки; AD – луч, падающий на верхнюю поверхность под малым углом α. Из рисунка

видно, что точка В будет мнимым изображением точки А.

240

Рассмотрим ACD : АС = CD , или, поскольку АС = h и CD = d, то tg

h d . Отрезок d найдем из BCD : CD = СВ tg β, или, учитывая, что tg

CD = d и CD = h1, имеем d = h1tg β . Тогда h = h1 tg . Поскольку углы α и β tg

малы, отношение тангенсов этих углов можно заменить отношением их

синусов, т.е.	tg	sin	. Следовательно, h = h1	sin	. Но по закону
	tg

		sin		sin

преломления sin = nв sin nc

ния воздуха nв = l. Тогда

Ответ: h = 0,06 м.

= 1 , так как абсолютный показатель преломле- nc

h = h1nс; h = 0,06 м.

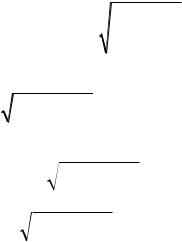
		Пример 5. Луч света падает на переднюю грань трехгранной призмы
	с преломляющим углом φ. После преломления он попадает на заднюю
	грань призмы и выходит в воздух. Определите угол отклонения светового
	луча , если угол падения луча на переднюю грань равен α, а абсолютный
	показатель преломления материала призмы n. (Уровень 4).
					Решение: Ход луча в призме показан на
			B		рисунке.	Как	внешний		угол	к	АЕC угол
					отклонения равен
						(i1 r1) (r2 i2 )					(1)
			E			(i1 r1) (r2 i2 )					(1)
i	A	r1	C	r2	Кроме того, AВC = ADK =						как углы,
i	A	r1	C		Кроме того, AВC = ADK =						как углы,
1		D	i2		образованные		взаимно		перпендикулярными
	K				образованные		взаимно		перпендикулярными
					сторонами .Угол ADK				является		внешним
					сторонами .Угол ADK				является		внешним
		Рис. 2.22			углом к	ADC ,поэтому
		Рис. 2.22					i2 r1				(2)
							i2 r1				(2)
	Из уравнений (1) и (2) получим
					i1 r2						(3)
Согласно закону преломления можно записать
					sini1 n ,		sini2	1 .			(4)
					sin r1		sin r2	n

241

Из уравнения (2) i2 r1 , поэтому

sin r2 nsin n sin cosr1 sin r1 cos .

Подставим в эту формулу значение sin r1 из (4):

	sini						sin	2 i
sin r		1		и cos r		1		1	.
sin r				и cos r		1			.
1	n				1		n2
	n						n2
Тогда

sin r sin			n	2 sin	2 i	cos sini				(5)
2					1			1

Сучетом уравнений (3) и (5) получаем выражение для угла δ:

i1 arcsin sin n2 sin2 i1 cos sini1 .

Ответ: i1 arcsin sin n2 sin2 i1 cos sini1 .

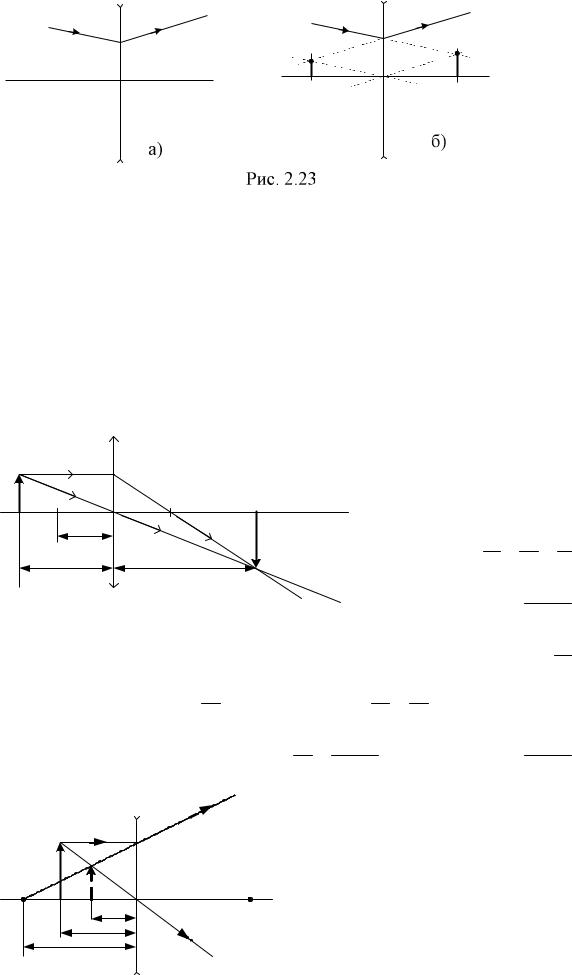
Пример 6. На рисунке 2.23 а) показан ход луча до и после его преломления в рассеивающей линзе. Найдите построением положение главных фокусов линзы. (Уровень 2).

Решение. Проведем побочную ось M M (рис. 2.23 б)), параллельную падающему лучу АВ. В рассеивающей линзе все лучи, параллельные данной оси M M , после преломления пойдут так, что их продолжения пересекутся в одной точке – побочном фокусе F'. Следовательно, если продолжим преломленный луч ВС до пересечения с побочной оптической осью M M , то найдём побочный фокус F'. Проведем через него фокальную плоскость, перпендикулярную главной оптической оси ММ, и

точка пересечения этой плоскости с главной осью и есть главный передний фокус линзы F, так как все фокусы лежат в фокальной плоскости, а

главный фокус - на главной оптической оси.

242

	A
	C
	B
M	M

	A			C
M F				C
M F			B	F M
M	F	M	M	F	M

Для нахождения заднего фокуса проводим побочную ось

M M

параллельную преломленному лучу ВС. Продолжим падающий луч АВ до

и находим соответствующий побочный фокус

пересечения с осью M M

F . Проводим фокальную плоскость и находим задний побочный фокус F.

Пример 7. Предмет высотой 4 м находится на расстояние 6 м от

оптического центра собирающей линзы с фокусным расстоянием 2 м.

Определите

высоту изображения

предмета.

Постройте

ход

лучей.

(Уровень 2).

Решение.

Построение

изображения

H предмета h приведено на

f O

рисунке

2.24.

Формула

тонкой линзы

1 1 .

Откуда

fa1

Рис. 2.24

a1 f

увеличение линзы

Г H .

С другой стороны, Г a2

. Следовательно, H a2 .

Подставим сюда

найденное значение a2 , получим

f .

Откуда

;

a1 f

H= 2 м.

Ответ: H= 2 м.

Пример 8. Предмет находится на

расстоянии

см

от

линзы

243

Рис. 2.25

оптической силой -5 дптр. На каком расстоянии человек, глядя через эту линзу, увидит изображение предмета и каким оно будет? (Уровень 2).

Решение. Так как D<O, то линза – рассеивающая (рис. 2.25). Для рассеивающей линзы формула тонкой линзы имеет вид

D .

a1 a2

Отсюда расстояние от линзы до изображения

1 a D

Подставив числовые значения, получим

a2 = 6 см.

Линейное увеличение

Г =

;

Г = 0,6.

Ответ: Г =

;

Г = 0,6.

Пример 9. Поместив на расстоянии 20 см от линзы свечу, получили на экране изображение свечи, увеличенное в 10 раз. Какое будет увеличение, если вплотную к данной линзе приложить линзу с оптической силой 2,5 дптр? -2,5 дптр? (Уровень 4).

Решение. По формуле тонкой линзы D0	=	1	1	, где D0 –

		a1 a2

оптическая сила первой линзы. Линейное увеличение Г a2 . Отсюда a1

a2 Гa1.

Тогда D0			=	1	1		. Оптическая сила двух собирающих линз
Тогда D0			=				. Оптическая сила двух собирающих линз
				a		Гa
			1		1						1	1
D' = D0 + Dl. Поэтому D0										+ Dl =	1	1				. Подставим вместо D0
D' = D0 + Dl. Поэтому D0										+ Dl =						. Подставим вместо D0
											a		Г a
найденное значение:										1		1			1
найденное значение:																			Г
	1	1	Dl			1		1		. Откуда Г1		=					1		Г		; Г1 = 1,7.
			Dl							. Откуда Г1		=			1						; Г1 = 1,7.
	a Гa					a Г a									1				1 Гa D
1		1			1			1	1					a1				D1	1	1
														a1			Гa	D1
																	1

Оптическая сила во втором случае D" = D0 - D2, где D2 – модуль

244

оптической силы. Тогда D" =			1		1			; D0 - D2 =	1		1		.
оптической силы. Тогда D" =				Г				; D0 - D2 =		Г			.
			a	Г	2	a			a	Г	2	a
	Г		1		2		1		1		2	1
Следовательно, Г2 =	Г		; Г2 = 2,5.
Следовательно, Г2 =	1 Гa D		; Г2 = 2,5.
	1 Гa D
	1	1

Ответ: Г2 = 2,5.

245

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2526 / 3526 27 28 29 30 31 32 33 34 35 > Следующая >>>

Соседние файлы в предмете Физика

#
18.02.202313.78 Кб0Л2.xlsx
#
18.02.2023572.75 Кб10Л3.docx
#
18.02.202317.5 Кб1Л3.xlsx
#
18.02.2023373.66 Кб1Л4.docx
#
18.02.202313.08 Кб1Л4.xlsx
#
18.02.20234.32 Mб12С.А.Вабищевич, В.А.Груздев, Г.А.Дубченок, В.Г.Залесский, Г.М.Макаренко Учебно-методический комплекс по общей физике. Часть 2.pdf
#
18.02.20231.95 Mб6С.А.Вабищевич, Н.В.Вабищевич, Н.А.Опарина Учебно-методический комплекс по общей физике. Часть 3.pdf