1278 / 2А135 / дополнительно / РПЗ часть

СОДЕРЖАНИЕ

Введение…………………………………………………………………………. 4

1 Вертикально – сверлильный станок 2А135…………………………………... 5

2 Кинематический расчёт……………………………………………………… 6

3 Расчёт зубчатых колёс…………………………………………………………14

4 Расчёт опорных реакций, статической и динамической грузоподъёмности подшипников и изгибающих моментов вала…………………………………..22

5 Расчёт сечения сплошного вала на статическую прочность

и выносливость…………………………………………………………………..26

6 Определение деформации кручения…………………………………………35

7 Экономическое обоснование…………………………………………………36

Заключение………………………………………………………………………37

Список использованных источников…………………………………………..38

ВВЕДЕНИЕ

В современном машиностроении большую долю всего оборудования составляют сверлильные станки, они незаменимы для обработки неточных отверстий, для черновой обработки и т.д., поэтому изучение конструкции данной группы станков является одним из важных этапов подготовки инженеров.

Темой курсового проекта предусматривается конструкторская разработка и полный расчёт привода главного движения вертикально – сверлиьного станка 2А135.

Была проведена работа по модернизации станка для использования более мощного двигателя и новых значений частоты вращения шпинделя. Такая модернизация даёт возможность производить сверление отверстий с большим диаметром и вести обработку более прочных материалов.

1 ВЕРТИКАЛЬНО – СВЕРЛИЛЬНЫЙ СТАНОК 2А135

Основные характеристики станка:

- наибольший условный диаметр сверления в стали 25 мм;

- рабочая поверхность стола 400×500 мм;

- наибольшее расстояние от торца шпинделя до рабочей поверхности стола 700 мм;

- вылет шпинделя 250 мм;

- наибольший ход шпинделя 200 мм;

- наибольшее вертикальное перемещение:

- сверлильной головки 170 мм;

- стола 270 мм;

- конус Морзе отверстия шпинделя 3;

- число скоростей шпинделя 9;

- частота вращения шпинделя 15 – 1000 мин^-1;

- число подач шпинделя 9;

- подача шпинделя 0,1…1,6 мм/об;

- мощность электродвигателя привода главного движения 2,0 кВт;

- габаритные размеры:

- длина 915 мм;

- ширина 785 мм;

- высота 2350 мм.

- масса 880 кг.

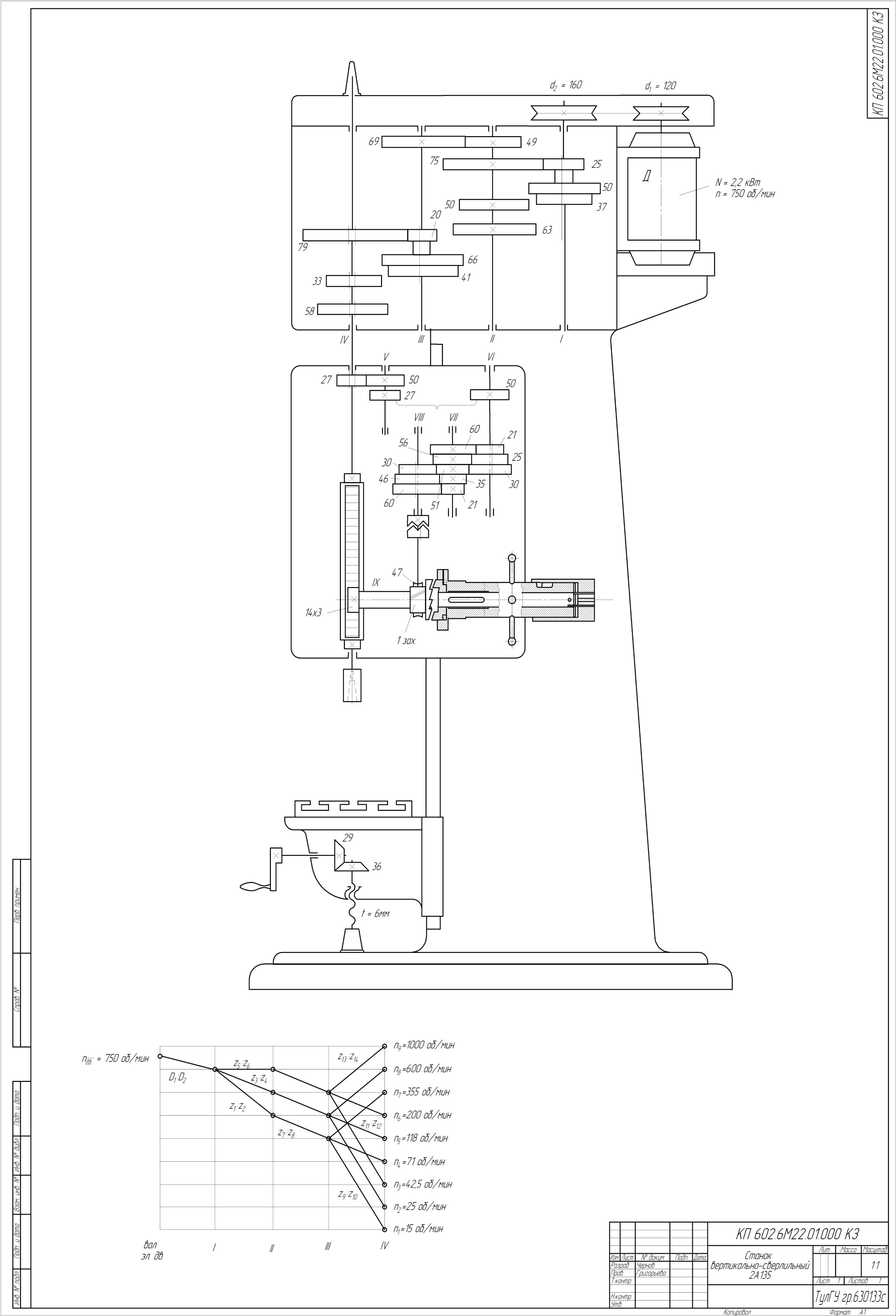
2 КИНЕМАТИЧЕСКИЙ РАСЧЁТ

2.1.Определение показателя геометрического ряда чисел оборотов шпинделя.

Показатель геометрического ряда чисел оборотов шпинделя подсчитывается по формуле:

.

Для n_max=1000 об/мин, n_min=63 об/мин и Z=9:

.

Полученное значение равно стандартному значению – 1,78.

2.2.Выбор структуры привода.

Для случая Z=9 при структуре могут быть два варианта порядка переключения групп передач, чему соответствуют две развёрнутые структурные формулы:

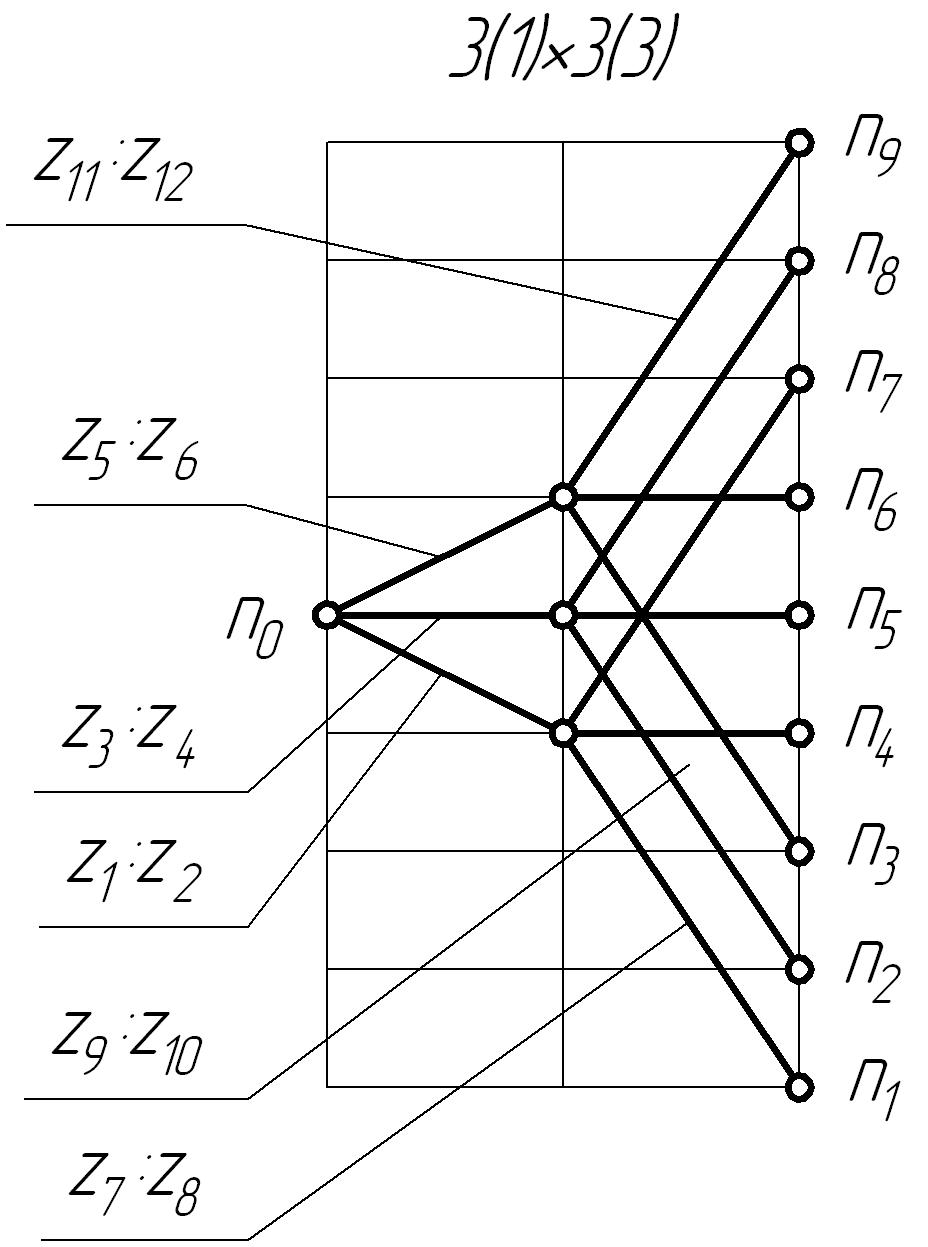
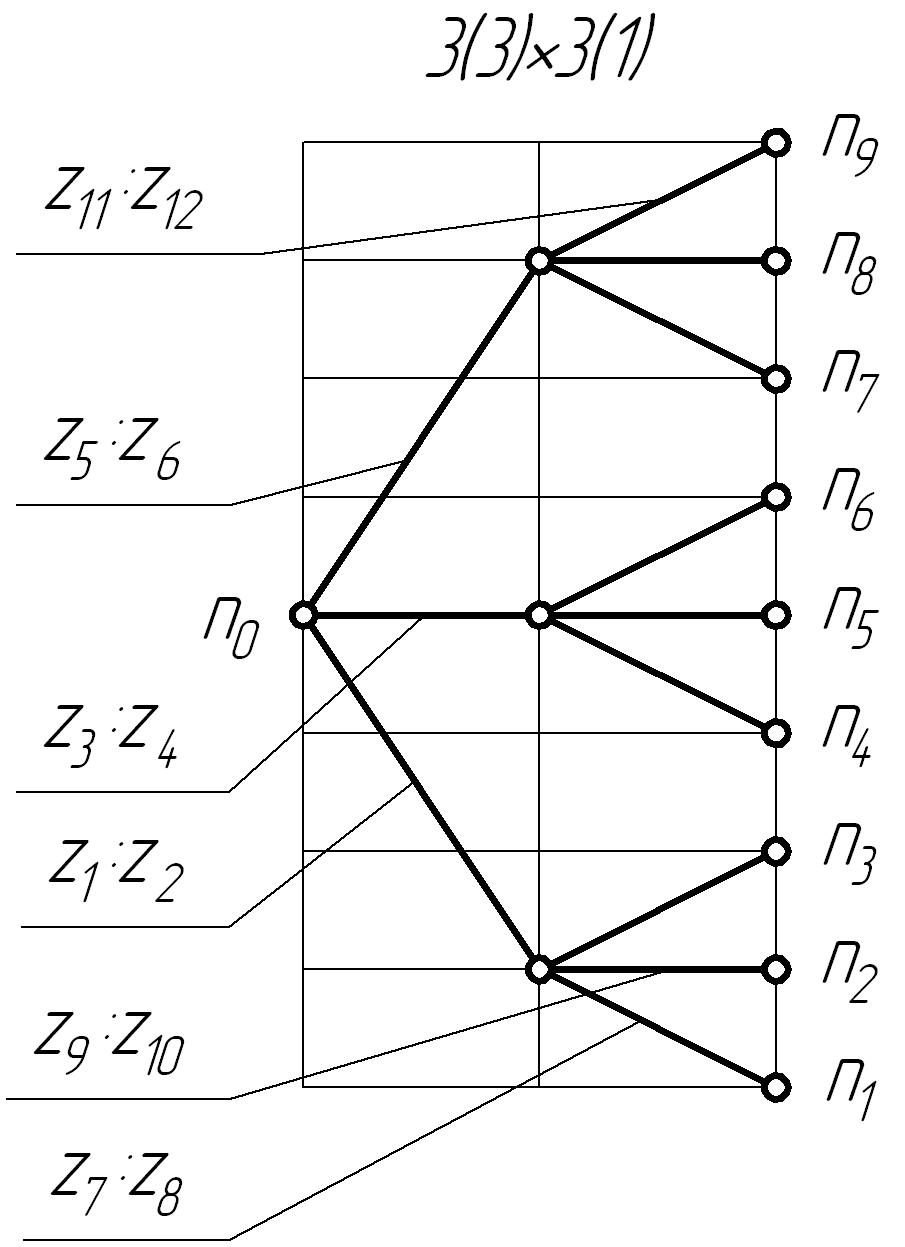
С целью наглядного представления и выбора оптимальной структуры привода следует изобразить возможные структурные сетки для принятой кинематической схемы.

По развёрнутым структурным формулам можно построить следующие структурные сетки.

Рисунок 1	Рисунок 2

Не все возможные варианты структурных сеток позволяют получить при разработке коробки скоростей компактное конструкторское решение. Это зависит от наибольшего значения показателя ряда, допускаемого той или иной сеткой. Поэтому после построения сеток производится анализ их с целью определения наибольшего допустимого каждой сеткой значения показателя . Практикой для коробок скоростей установлены следующие рекомендуемые значения передаточных отношений для любой группы передач:

При выполнении этих условий получаем следующее выражение для :

.

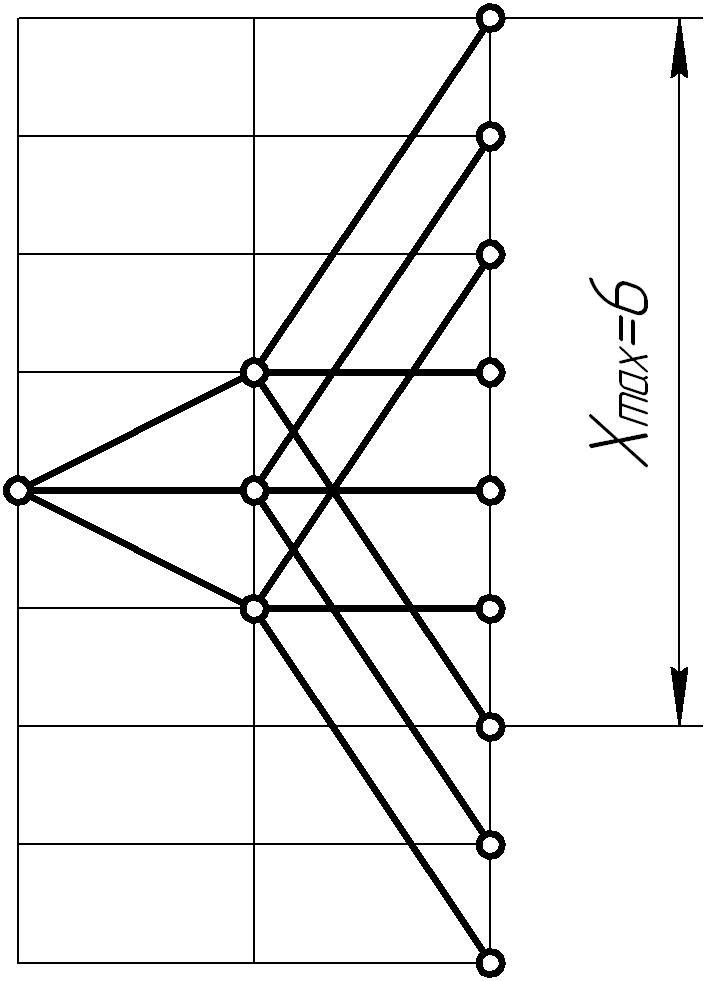
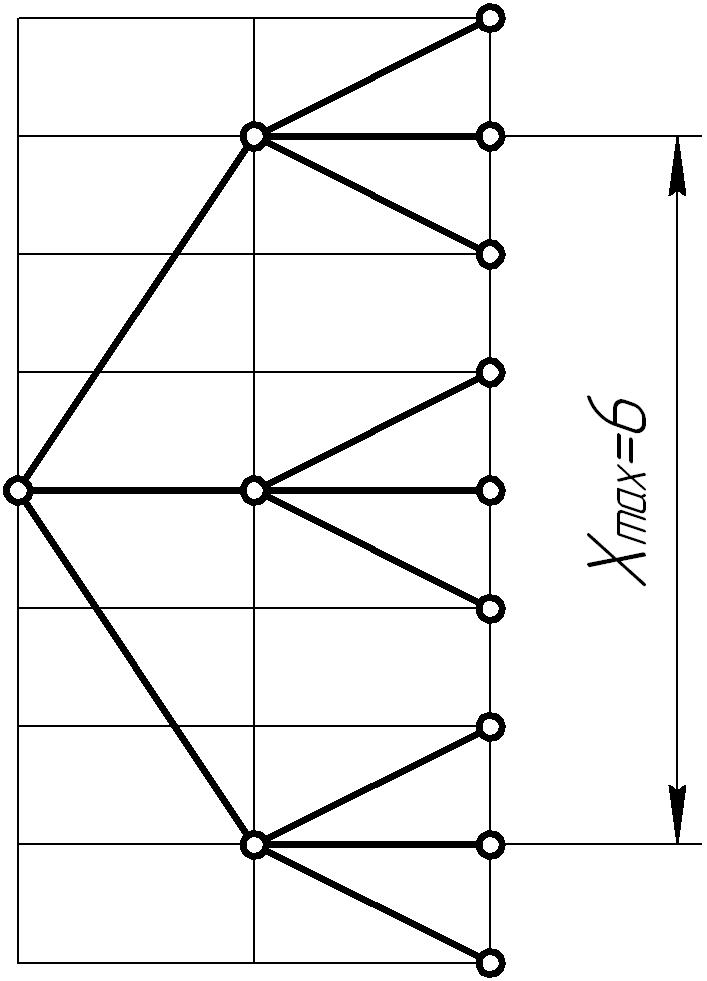
В данном приводе X_max=6, поэтому имеем:

.

Рисунок 3	Рисунок 4

С точки зрения компактного исполнения привода приемлемы сетки, для которых выдерживается условие:

.

Данное условие выполняется, т.к. вычисленный показатель геометрического ряда меньше максимального , т.е. выполняется условие компактного исполнения привода.

2.3.Определение абсолютных величин передаточных отношений.

Для определения действительных чисел оборотов, которые имеют все валы привода, и абсолютных передаточных отношений групповых и одиночных передач строится диаграмма (картина, график) чисел оборотов (ДЧО). ДЧО выполняется на весь привод, т.е. на групповые и одиночные передачи. Построение ДЧО возможно, если известно число оборотов электродвигателя.

2.3.1.Выбор электродвигателя.

Учитывая исходные данные и выбранную структуру привода выбираем электродвигатель112МА8, мощностью P=2,0 кВт, n=750 об/мин.

2.3.2.Производим разбивку передаточного отношения и определяем передаточные отношения.

Разбивка производится для того, чтобы быть уверенным, что минимальное передаточное отношение каждой передачи не выходит за пределы допустимого, т.е.:

Производим разбивку .

Для первой умножающей группы можно построить следующие структурные графики:

Рисунок 5	Рисунок 6	Рисунок 7	Рисунок 8	Рисунок 9

Для основной группы возможен лишь один вариант:

Рисунок 10

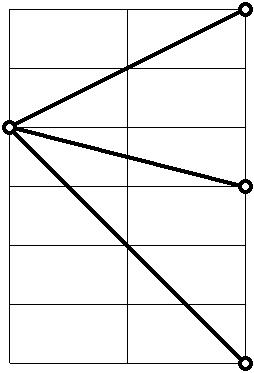
Выбираем для умножающей группы вариант, изображённый на рисунке 6.

Исходя из полученных данных строим ДЧО.

Рисунок 11

Определяем передаточные отношения:

Компоновка привода главного движения:

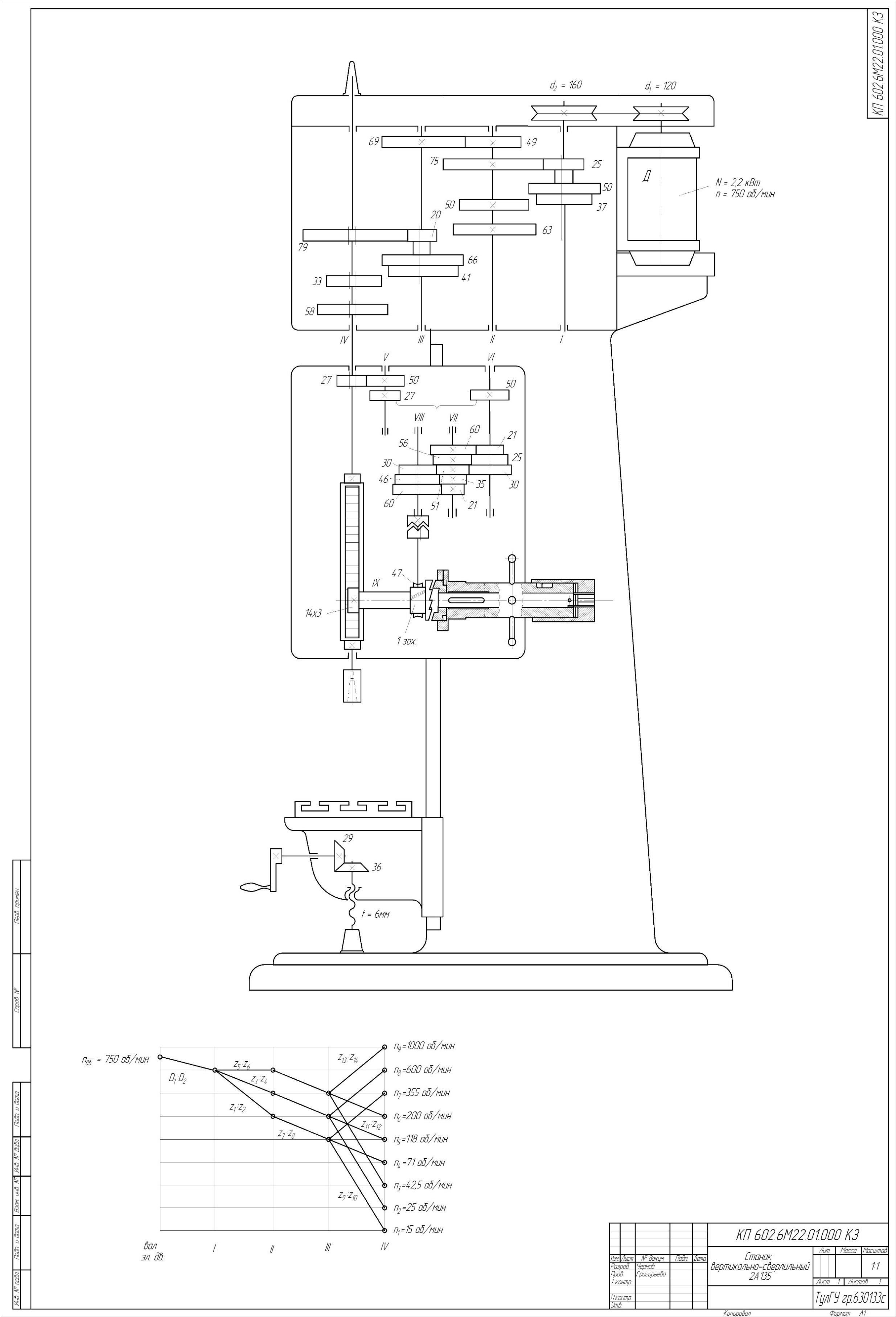
Рисунок 12

2.4. Расчёт диаметров шкивов.

Вал асинхронного двигателя делает меньше оборотов в минуту, чем магнитное поле статора. Поэтому диаметры шкивов ременной передачи подбираются из действительных чисел оборотов.

Исходя из выше приведенного принимаем диаметры шкивов 120 мм и 160мм.

2.5. Расчёт чисел зубьев шестерен.

2.5.1. Расчёт чисел зубьев шестерен.

Существуют несколько методов расчёта чисел зубьев групповых передач:

- метод наименьшего кратного;

- табличный метод;

- расчёт на ЭВМ.

Наиболее простой из трёх представленных это третий метод – расчёт на ЭВМ, поэтому в данном курсовом проекте используем именного его.

Имея в качестве исходных данных передаточные отношения и типы передач производим расчёт чисел зубьев передач (см. выше).

Полученные результаты:

2.5.2. Соотношения между числами зубьев колёс передвижных блоков.

В данном приводе две группы, состоящие из трёх зубчатых передач и их включение и выключение производится посредством передвижного (скользящего) «узкого» тройного зубчатого блока, поэтому найденные числа зубьев этой группы необходимо проверить на возможность свободного перевода блока во все требуемые положения.

Для того, чтобы блок их трёх колёс Z₁> Z₃> Z₅ можно было перевести влево до зацепления Z₁ с Z₂, колесо Z₃ должно свободно пройти мимо колеса Z₆. При некоррегированных колесах «узкий» тройной блок можно переключить во все положения при условии:

.

Для первого тройного блока имеем:

,

следовательно условие успешного переключения соблюдается.

Для второго тройного блока:

,

следовательно условие успешного переключения соблюдается.

13