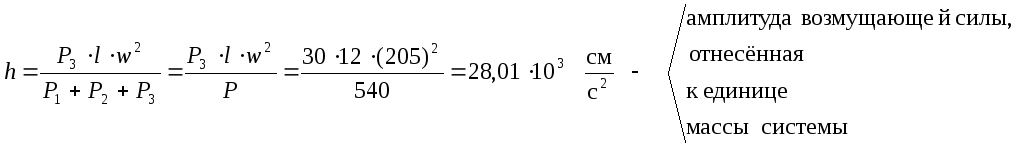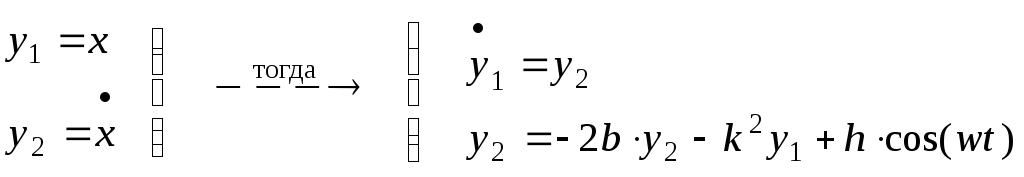RGR_po_TM_33_MOYa_33
.doc|
Исследование прямолинейных колебаний платформы Задание: Дана схема механической системы, состоящей из платформы, электродвигателя, установленного на платформе, эксцентричной массы на валу электродвигателя. Исходные данные приведены в таблице: |
||||||||||||||
|
|
Сила тяжести, Н |
Линейный размер, см |
Коэфф-т жёсткости |
Коэфф-т затухания |
Угловая скорость |
Время работы |
|
|||||||
|
|
P1 |
P2 |
P3 |
a |
l |
c (кН/см) |
b (c –1) |
b (c –1) |
b (c –1) |
(c –1) |
t1 (c) |
|
||
|
|
60 |
450 |
30 |
32 |
12 |
2,4 |
0 |
32 |
52 |
205 |
0,1 |
|
||
|
Требуется:
|
||||||||||||||
|
|
|
|||||||||||||
|
|
||||||||||||||
|
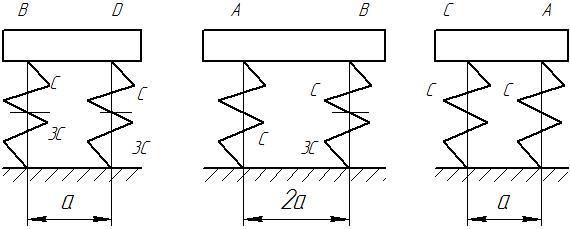
Для четырёх опор эквивалентная пружина имеет жёсткость:
В точке А с платформой свяжем прямоугольную систему координат AX1Y1Z1, оси AY1, AZ1 которой параллельны соответственно осям OY и OZ; ось АХ1 совпадает с осью ОХ.
В положении статического равновесия
упругая сила эквивалентной пружины
уравновесит суммарную силу тяжести
платформы Р1, электродвигателя Р2
и эксцентричной массы Р3, т.е.
Отсюда находим величину статического отклонения платформы:
|
||||||||||||||
|
|
|
|||||||||||||
|
|
||||||||||||||
|
Координаты у2, z2 центра масс электродвигателя находим из условий:
В этом случае расстояние между центром масс электродвигателя и точкой крепления эксцентричной массы определяем по формуле:
|
||||||||||||||
|
|
|
|||||||||||||
|
|
||||||||||||||
|
где а1, а2, а3 – ускорения центров масс платформы, электродвигателя, эксцентричной массы; g – ускорение силы тяжести; FЭ – эквивалентная упругая сила. Проектируя левую и правую части векторного уравнения на ось ОХ, имеем:
Так как в положении статического
равновесия платформы имеет место
равенство:
Поделив
левую и правую части на
|
||||
|
получаем неоднородное дифференциальное
уравнение, описывающее вертикальные
незатухающие колебания платформы:
Дифференциальное
уравнение, описывающее вынужденные
колебания с учётом сопротивления
|
||||
|
|
|
|
||
|
|
|
|||
|
или
где
|
||||
|
|
|
|||
|
|
||||
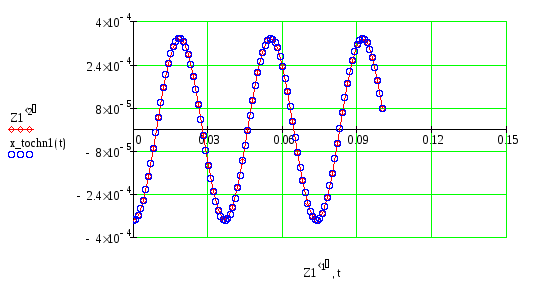
Дифференциальные уравнения, описывающие
прямолинейные колебания платформы,
вызванные возмущающей силой
Для определения закона движения решаем систему уравнений первого порядка. При решении используем программу «Решение системы дифференциальных уравнений методом Рунге-Кутта (прямолинейные колебания платформы)», составленную для персонального компьютера.
Начальными данными для решения
уравнений при t=0
являются:
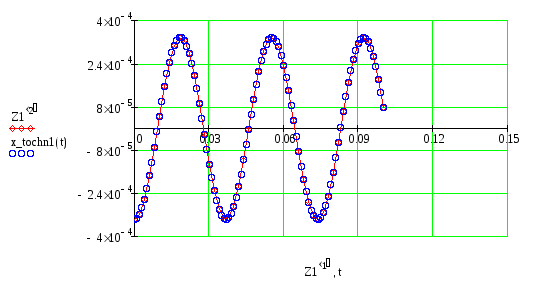
Результат решения используем для построения графика свободных незатухающих прямолинейных колебаний платформы. График представлен в приложении 1.
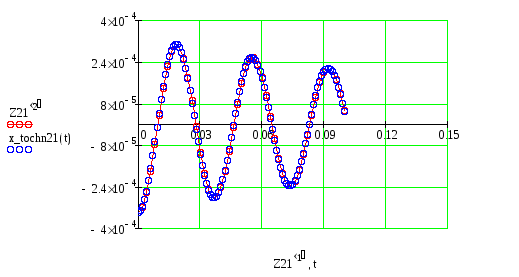
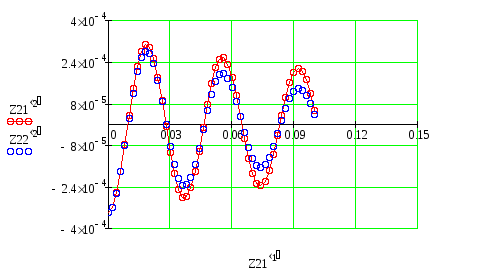
Начальное и конечное значения аргумента: 0 и 0,1. Используя полученное решение строим графики затухающих колебаний платформы при b=32 c–1 и b=52 c–1 (приложение 2).
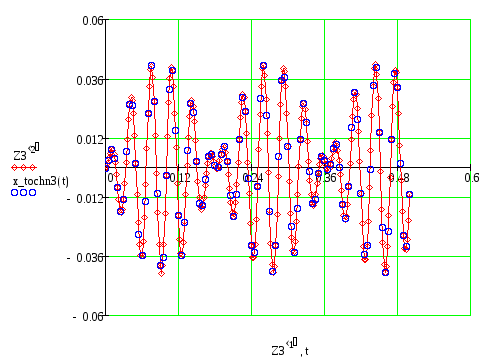
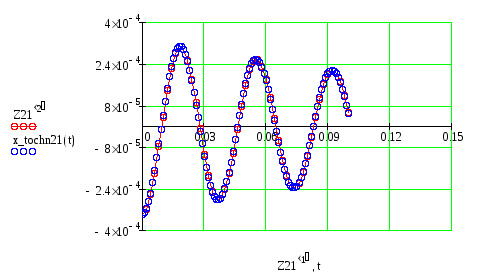
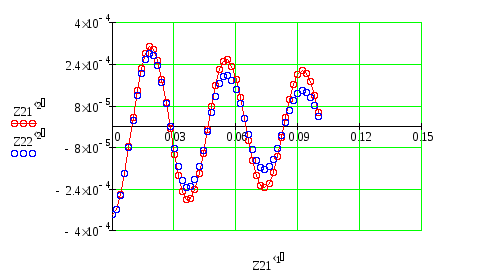
Начальные значения функций у(1) и у(2) при t=0 принимаются равными 0. Результаты решения используем для построения графиков вынужденных колебаний платформы при b=0, b=32 с–1 и b=52 с–1 . Графики представлены в приложении 3.
|
||||
|
|
|
|||
|
|
||||
|
При составлении программы вычислений
коэффициента динамичности колебаний
воспользуемся уравнением
После нескольких преобразований получаем формулы для вычисления коэффициента динамичности и фазовой характеристики
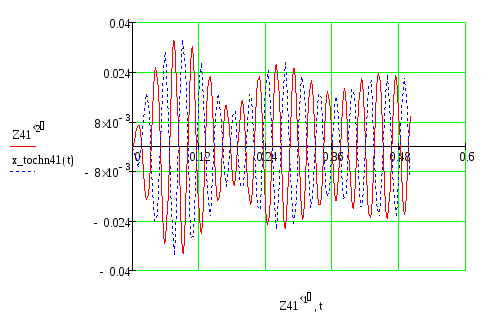
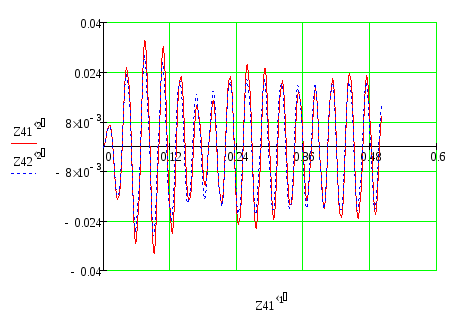
Результаты вычислений и оформляем в виде графиков, представленных в приложениях 4 и 5. Графики коэффициентов динамичности и фазовой характеристики построены для значений b=0, b=32 с–1 и b=52 с–1 .
|
||||
|
|
|
|||
|
|
||||
|
Библиографический список.
Яблонский А.А. и др. Курс теоретической механики. Ч. 2 – М.: Высш. шк., 1971. |
||||
|
|
|
|||
|
|
||||
|
Приложение 1
Продолжение приложения 1
Приложение 2
Приложение 3
Продолжение приложения 3
Продолжение приложения 3
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
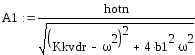
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

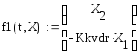
![]()
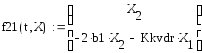
![]()
![]()
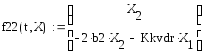
![]()
![]()
![]()
![]()
![]()
![]()
![]()
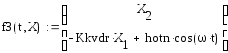
![]()

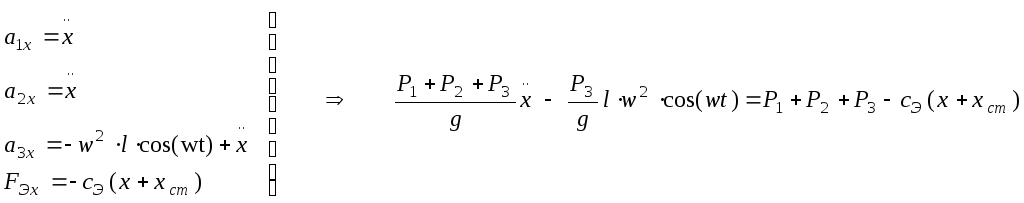

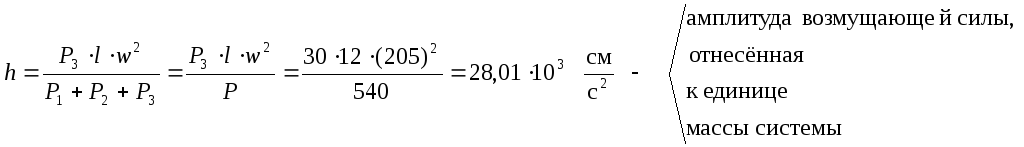 получаем
неоднородное дифференциальное
уравнение, описывающее вертикальные
незатухающие колебания платформы:
получаем
неоднородное дифференциальное
уравнение, описывающее вертикальные
незатухающие колебания платформы: