Наклона: а) в диметрии; б) на эпюре
В
прямоугольном треугольнике АВВ
- катет АВ
= АнВн;
катет ВВ
=
Zв
– Zа
= ∆Z;
гипотенуза АВ
– натуральная величина отрезка, α
– угол наклона прямой АВ
к плоскости Н.
В прямоугольном треугольнике АВА - сторона А В = AvBv; сторона А А = Yа – Yв = ∆Y; сторона АВ – натуральная величина отрезка; β – угол наклона прямой к плоскости V.
2.2.4. Следы прямой линии
Точки пересечения прямой линии с плоскостями проекций называют следами прямой линии (Рис.2.8а, б).
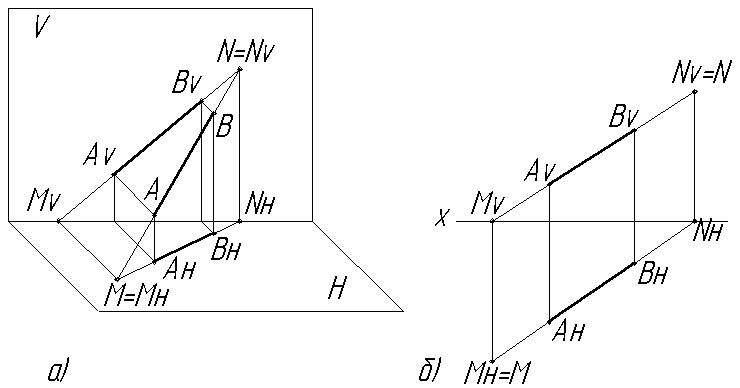
Рис. 2.8. Следы прямой: а) в диметрии; б) на эпюре
Продолжим прямую АВ до пересечения с плоскостью Н. Получим точку М, которая является горизонтальным следом прямой. Продолжая прямую АВ до пересечения с плоскостью V получим точку N – фронтальный след прямой.
Чтобы на эпюре найти горизонтальный след, необходимо продолжить фронтальную проекцию AvBv до пересечения с осью Х; через точку пересечения Мv (фронтальную проекцию горизонтального следа) провести перпендикуляр к оси Х до пересечения с продолжением горизонтальной проекции прямой АнВн. Точка пересечения Мн является горизонтальной проекцией горизонтального следа (она совпадает с самим следом М).
Для нахождения фронтального следа необходимо продолжить горизонтальную проекцию АнВн до пересечения с осью Х; через точку Nн (горизонтальную проекцию фронтального следа) провести перпендикуляр до пересечения с продолжением фронтальной проекции AvBv. Точка Nv является фронтальной проекцией фронтального следа (она совпадает с точкой N – самим фронтальным следом прямой).
2.3. Взаимное положение прямых линий
Если прямые параллельны, то их одноименные проекции параллельны.
Если прямые линии пересекаются, то их одноименные проекции пересекаются между собой в точках, которые являются проекциями точки пересечения этих прямых.
Скрещивающиеся прямые линии не пересекаются и не параллельны между собой, хотя проекции их могут пересекаться или быть параллельными.
Точки пересечения этих проекций не лежат на одной линии связи. Одной точке 1v соответствуют две точки 1н и 1'н. Эти точки лежат на одном перпендикуляре к плоскости V (Рис.2.9а, б, в).
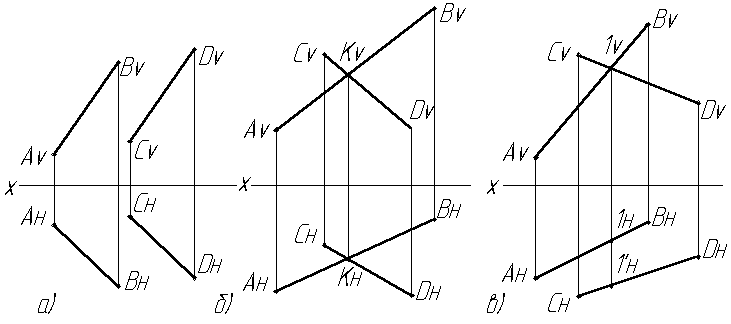
Рис. 2.9. Взаимное положение отрезков на эпюре:
А) параллельные; б) пересекающиеся; в) скрещивающиеся
2.3.1. Конкурирующие точки
Точки, лежащие на одном перпендикуляре к плоскости проекций, называются конкурирующими относительно этой плоскости (Рис.2.10а, б).
По конкурирующим точкам определяется видимость геометрических образов на эпюре. Видимой на данной проекции всегда будет та из конкурирующих точек, которая лежит дальше от этой плоскости проекций, следовательно, ближе к зрителю. Точки А и В являются фронтально конкурирующими. На фронтальной плоскости проекции будет видима точка А, т.к. она дальше от плоскости V и ближе к наблюдателю. Точки А и С – горизонтально конкурирующие. На горизонтальной плоскости проекций будет видима также точка А, т.к. она отстоит от плоскости Н дальше, чем точка С.
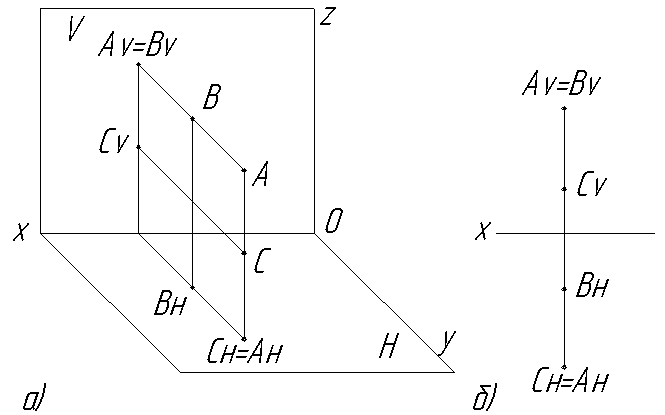
Рис. 2.10. Конкурирующие точки: а) в диметрии; б) на эпюре