2.2.1. Прямые частного положения

К прямым частного положения относятся линии уровня – прямые, параллельные одной из плоскостей проекций, и проецирующие линии – прямые, перпендикулярные к одной из плоскостей проекций.

У куба с вырезом (Рис.2.4) линии, расположенные в гранях куба, параллельны плоскостям проекций будут линиями уровня.

Линия, параллельная горизонтальной плоскости проекций, называется горизонталью и на эпюре обозначается буквой h.

Линия, параллельная фронтальной плоскости проекций, называется фронталью и обозначается буквой f.

Линия, параллельная профильной плоскости проекций, называется профильной прямой и обозначается буквой р.

Ребра куба, стоящего на плоскости Н так, как это показано на рис. 2.4, параллельны двум плоскостям проекций и перпендикулярны третьей. Их направление совпадает с направлением проецирующих прямых при прямоугольном проецировании. В зависимости от перпендикулярности к той или иной плоскости проекций, прямые называются:

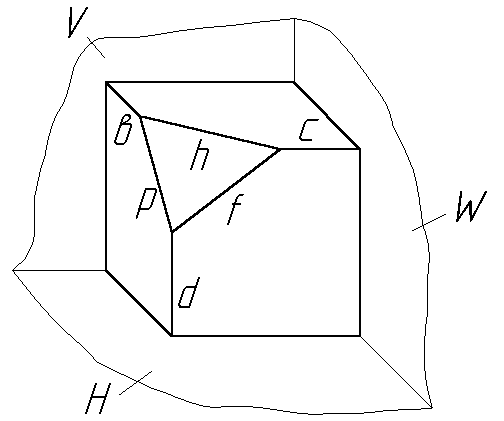
Рис 2.4 Прямые частного положения

• линия, перпендикулярная горизонтальной плоскости проекций Н, называется – горизонтально проецирующей прямой (прямая d);

• линия, перпендикулярная фронтальной плоскости проекций V, называется фронтально проецирующей прямой (прямая в);

• линия, перпендикулярная профильной плоскости проекций W, называется профильно проецирующей прямой (прямая с).

На рис.2.5 даны возможные положения прямых в системе плоскостей проекций в наглядном изображении и на эпюре. Фронтальная проекция горизонтали параллельна оси проекции Х, а на горизонтальной плоскости проекций она изображается в натуральную величину. На горизонтальной же проекции угол наклона горизонтали к фронтальной плоскости проекций изображается в натуральную величину. Аналогичны рассуждения относительно фронтали и профильной прямой.

Угол между прямой и плоскостью определяется углом между прямой и ее проекцией на эту плоскость. Угол наклона прямой к горизонтальной плоскости проекций обозначается - , к фронтальной - , к профильной - .

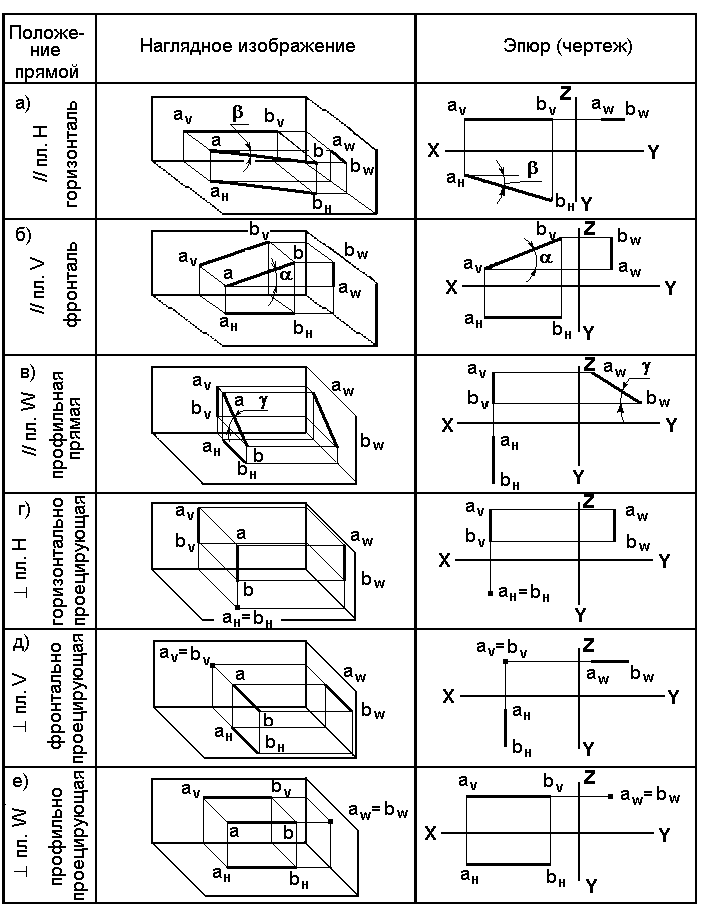
Рис 2.5 Проекция прямой частного положения

2.2.2. Прямая общего положения

Прямая, непараллельная ни одной из плоскостей проекций, называется прямой общего положения (Рис.2.6а, б).

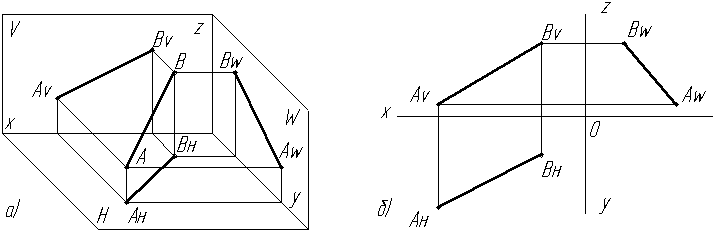
Рис. 2.6 Прямая общего положения:

а)- в диметрии; б)- на эпюре

По проекциям отрезка прямой общего положения можно представить себе положение этого отрезка в пространстве. Однако, ни одна из проекций отрезка прямой общего положения не дает его натуральной величины и углов наклона к плоскостям проекций.

2.2.3 Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций

Натуральная величина отрезка прямой всегда может быть принята за гипотенузу прямоугольного треугольника, одним катетом которого является отрезок, равный и параллельный проекции, а другим – разность расстояний концов отрезка до плоскости проекций (Рис.2.7а, б).

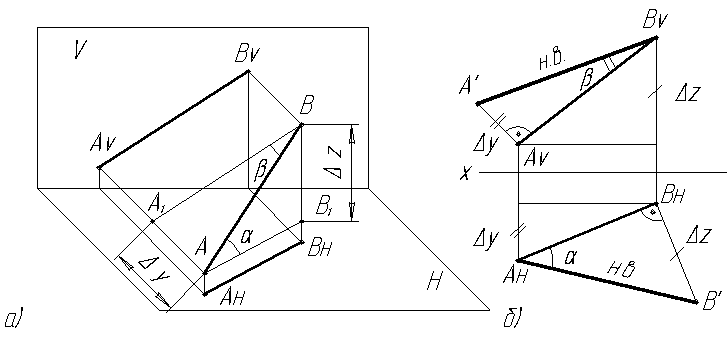
Рис. 2.7. Определение натуральной величины отрезка и углов