Глава 2. Точка, прямая, плоскость

2.1. Ортогональные проекции точки

Прямоугольные проекции на две или три взаимно перпендикулярные плоскости принято называть ортогональными.

Зададим три взаимно перпендикулярные плоскости проекций и точку А в пространстве (Рис.2.1).

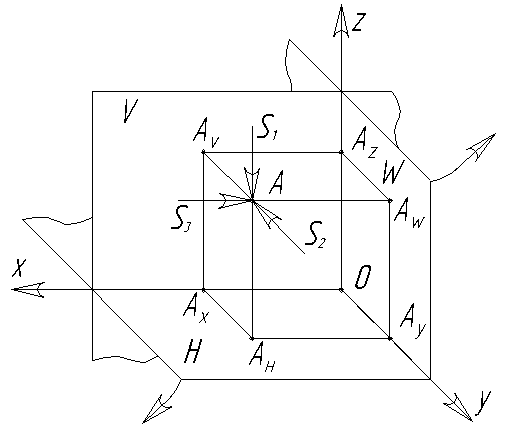
Рис. 2.1. Ортогональные проекции точки

V, H, W – плоскости проекций

V – фронтальная плоскость проекций

H – горизонтальная плоскость проекций

W – профильная плоскость проекций

Линии пересечения плоскостей проекций X, Y, Z – оси проекций.

Для того, чтобы получить три проекции точки А, следует из нее опустить перпендикуляры на плоскости проекций. Точки пересечения перпендикуляров с плоскостью V – фронтальная проекция точки A_v, с плоскостью Н – горизонтальная проекция точки А_н, с плоскостью W – профильная проекция точки А_w.

Для перехода к плоскому чертежу, эпюру (от французского слова epure – чертеж, проект) нужно плоскость Н повернуть вниз вокруг оси Х до совмещения с плоскостью V, а плоскость W совместить с плоскостью V, поворачивая ее вокруг оси Z вправо (Рис.2.2а).

Две ортогональные проекции на взаимно перпендикулярные плоскости лежат на прямых, перпендикулярных к соответствующей оси проекции и пересекают эту ось в одной и той же точке. Эти линии называются линиями связи.

Расстояние от точки до плоскостей проекций называются координатами этой точки и могут быть измерены по осям.

1) Расстояние АА_w(ХА) от профильной плоскости проекций является абсциссой точки А;

2) Расстояние АА_v(YА) точки А от фронтальной плоскости проекций называется ординатой (на рис.2.1 размер оси Y уменьшен в два раза, т.к. во фронтальной диметрии показатель искажения равен 0,5);

3) Расстояние АА_н(ZА) точки А от горизонтальной плоскости проекций называется аппликатой точки А.

Точка может быть задана ее координатами X, Y, Z, например,

А ( , , )

Чертеж, на котором точка или система точек изображаются при совмещенном положении плоскостей проекций называется эпюром или чертежом.

Границы плоскостей проекций на эпюре обычно не показываются. Во многих случаях бывает достаточно двух плоскостей проекций, в этом случае проводится только одна ось проекции Х (Рис.2.2б).

2.1.1. Безосный эпюр

Изображения (проекции) точки, линии, плоской фигуры или пространственной формы на плоскостях проекций не изменятся, если плоскости перемещать по отношению к проецируемому объекту параллельно самим себе. При этом расстояния проецируемого объекта от плоскостей проекций изменяются, но это обстоятельство не имеет никакого значения для решения многих задач. Так, на технических чертежах оси проекций обычно не показывают. Поэтому на эпюре в ряде случаев можно не изображать осей проекций. Пример безосного чертежа точки приведен на рис.2.2в.

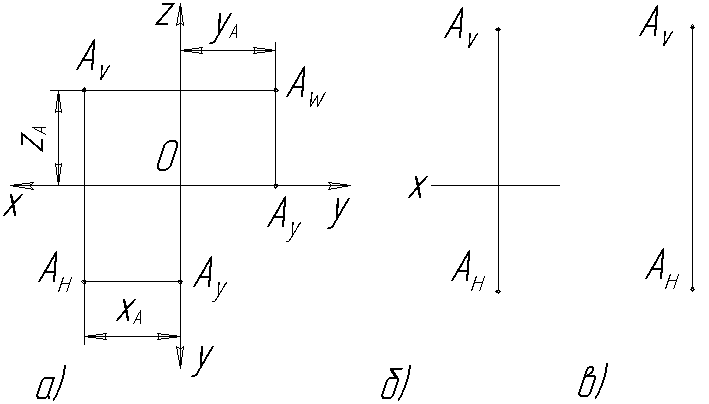
Рис. 2.2. Чертёж (эпюр) точки: а) на три плоскости проекции;

Б) на две плоскости проекции; в) безосный

2.2. Ортогональные проекции прямой

Чтобы построить проекции какой-либо линии, нужно задать проекции двух ее точек и соответствующие проекции этих точек соединить (Рис.2.3). Относительно плоскостей проекций прямые могут занимать частные или общие положения.

Рис. 2.3. Проекции отрезка прямой