1.4. Аксонометрические проекции

Одним из видов обратимых чертежей является аксонометрический чертеж.

Аксонометрическая проекция – это параллельная проекция предмета, связанного с осями координат, на одну плоскость, которая называется плоскостью аксонометрических проекций. Тогда на изображениях осей могут быть нанесены линейные (или числовые) масштабы, пользуясь которыми можно определить размеры оригинала по его изображению (Рис.1.10).

А – аксонометрическое изображение точки А₁; XYZ – аксонометрическое изображение натуральной системы координат X₁; Y₁; Z₁; S – направление проецирования; Р – плоскость аксонометрических проекций.

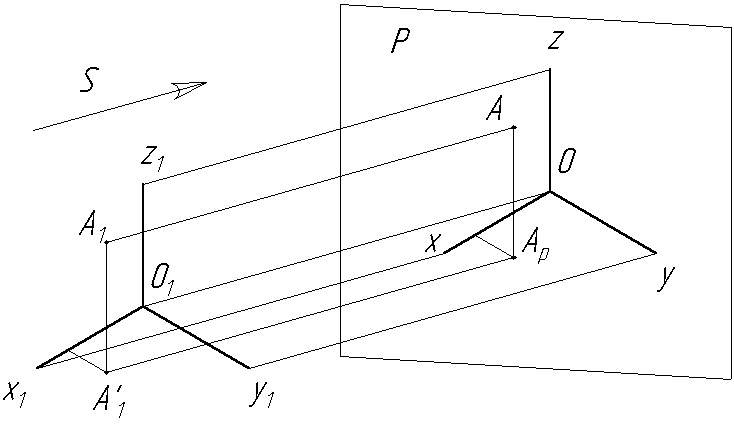
Рис. 1.10. Модель образования аксонометрического

Изображения точки

Аксонометрические проекции относятся к наглядным видам изображений. Для получения наглядности положения предмета относительно плоскости аксонометрических проекций и направление проецирования выбирается так, чтобы на чертеже были получены изображения всех трех измерений аксонометрических осей (Рис.1.11).

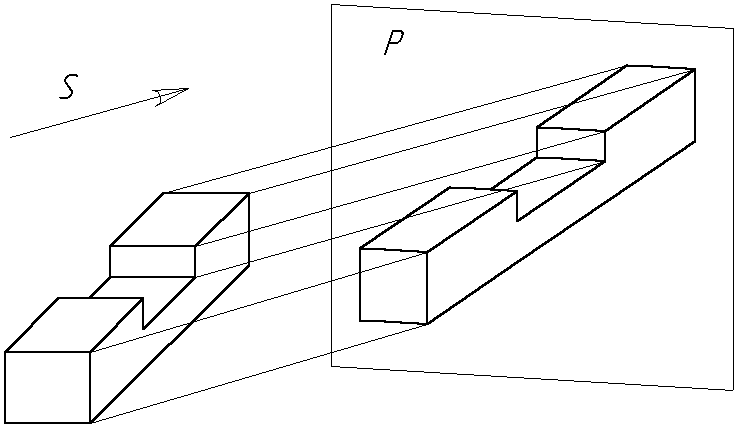
Рис 1.11. Аксонометрическое изображение модели

В зависимости от направления проецирования аксонометрические проекции делятся на прямоугольные и косоугольные.

В зависимости от показателей искажения по осям аксонометрические проекции делятся на изометрию (показатели искажения по всем трем осям одинаковы), диметрию (показатели искажения равны лишь по двум осям) и триметрию (показатели искажения по всем трем осям различны).

Аксонометрия

диметрия

триметрия

прямоугольная

косоугольная

изометрия

1.4.1.Направление аксонометрических осей и показатели

искажения

На рис.1.12. даны направления аксонометрических осей и показатели искажения для стандартных аксонометрических проекций.

Рис. 1.12. Направление аксонометрических осей и показатели искажения: а) изометрия прямоугольная; б) диметрия прямоугольная; в) диметрия косоугольная

XOZ – фронтальная плоскость V;

XOY – горизонтальная плоскость Н;

ZOY – профильная плоскость W.

Плоскости H, V, W в пространстве взаимно перпендикулярны.

Аксонометрическая проекция называется практической (или приведенной), если при ее построении используются практические показатели искажения. При применении практических показателей искажения по осям, в изометрии все изображение пропорционально увеличивается в 1,2 раза, а в диметрии в 1,06 раза.

1.4.2. Построение окружности в аксонометрических проекциях

Во всех аксонометрических проекциях окружности, лежащие в плоскостях проекций или в плоскостях им параллельных, проецируются в виде эллипсов. Только во фронтальной (косоугольной) диметрии окружность, лежащая во фронтальной плоскости, изображается без искажения.

Направление и размеры осей эллипсов в прямоугольных практических изометрии и диметрии приведены на рис.1.13.

Рис. 1.13. Направление осей элипсов в аксонометрии а) в изометрии прямоугольной; б) в диметрии прямоугольной; в) в диметрии косоугольной (фронтальной)

В прямоугольных аксонометрических проекциях большая ось эллипса всегда перпендикулярна отсутствующей аксонометрической оси, а малая – перпендикулярна к большой.