0842 / metod_ukazania_RGR

YF – коэффициент формы зуба, выбирают из таблицы 5.1 по эквивалентному числу зубьев:

61

[ ]F – допускаемое напряжение на изгиб, определяют из выражения (5.18) 6.1.11 Производят проверку прочности зубьев при кратковременных пере-

грузках по контактным напряжениям (5.20) и напряжениям изгиба (5.21). 6.2 Пример расчета конической зубчатой передачи

Рассчитать коническую прямозубую передачу одноступенчатого редуктора при следующих данных: крутящий момент по шестерне Т1 = 126·103 Н·мм; пе-

редаточное число и = 3,15; частота вращения шестерни n = 1000 мин –1; срок службы передачи t = 10000 ч; нагрузка постоянная; степень точности 8; коэф-

фициент кратковременной перегрузки = ТП / ТН = 1,8 .

Решение: материал зубчатых колес - шестерня – сталь 40Х улучшенная,

твердость поверхностей зубьев НВ = 250; колесо – сталь 45 улучшенная, НВ

=200; коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба КН =1,15; коэффициент, учитывающий динамические нагрузки

КНV = 1,2; коэффициент, учитывающий относительную длину зуба bRe =

0,285; число зубьев шестерни z1 = 25; колеса – z2 = 79.

Коэффициент нагрузки

КН = КН · КНV =1,15 ·1,2= 1,35,

коэффициент безопасности [SН] = 1,1;

коэффициен долговечности:

Принимаем КНL1=1.

Допускаемые напряжение на контактную прочность:

н = (2НВ + 70) · КНL1 / SН = (2·250 + 70) · 1/1,1 = 480 МПа .

Внешний делительный диаметр шестерни

de1 2 33352 T1 KH /[ Н ]2 (1 0,5 b Re )2 b Re u ,

62

de1 2 33352 126 103 1,35/ 4802 (1 0,5 0,285)2 0,285 3,15 99,15 мм 100 мм

Модуль зацепления

me = dei /z1 = 100/25 = 4 мм.

Это значение соответствует стандарту.

Геометрические параметры передачи:

углы делительных конусов

и = tg 2 = сtg 1 = 3,15, 1 = 17°34'; 2 = 72°26' ;

внешние делительные диаметры

dei = me · zi ,

de2 = 4 · 79 = 316 мм;

внешние диаметры окружностей выступов

deai = dei + 2 · me · cos i:

dea1 = 100 + 2 · 4 · cos 17°34' = 107,62 мм , dea2 = 316 + 2 · 4 · cos 72°26' = 319,36 мм ;

внешние диаметры окружностей впадин

defi = dei – 2,5 · me · cos i:

def1 = 100 – 2,5 · 4 · cos17°34' = 90,47 мм , def2 = 316 – 2,5 · 4 · сos72°26' = 311,8 мм;

внешнее конусное расстояние

Re 0,5 me z12 z22 0,5 4252 792 166 мм;

длина зуба

b = bRe ·Rе = 0,285 · 166 = 48 мм ;

средний делительный диаметр шестерни

d1 = 2(Re – 0,5b)· sin 1= 2(166 – 0,5·48)·sin17°34' = 85,77 мм .

Усилия в передаче:

окружное

Ft =2T1/d1=2·126·103/85,77 = 2940 Н;

63

радиальное усилие на шестерни равное осевому усилию на колесе

Fr1= –Fa2 = Ft1 · tg · cos 1 = 2940 · tg20° · cos17°34' = 1020 H;

осевое усилие на шестерни равное радиальному усилию на колесе

Fa1 = –Fr2= Ft · tg · sin 1 = 2940 · tg20° · sin 17°34' =322 Н .

Напряжение изгиба, возникающее в зубьях шестерни

F = Ft · КF ·YF / b · m ≤[ F] .

Параметры, входящие в данную формулу: коэффициент, учитывающий не-

равномерность распределения нагрузки по длине зуба КF =1,4; коэффициент,

учитывающий динамические нагрузки КFV =1,33. Поэтому

KF = КF · КFV = 1,4·1,33 = 1,86.

Коэффициент формы зуба YF выбирают по эквивалентному числу зубьев zV1 = z1/cos3 1 = 25 · cos317°34' ≈ 26.

По таблице 5.2 YF = 3,88.

Модуль средний

m = d1/z1 = 85,77/25 = 3,431 мм .

Допускаемое напряжение на изгиб зубьев шестерни

[ F] = 1,8НВ/ SF ' · SF ".

Коэффициент, учитывающий неоднородность материала, SF ' = 1,75, коэф-

фициент, учитывающий вид заготовки - для проката SF " = 1. Поэтому

[ F] = 1,8 · 250/1,75 · 1,0 = 257,143 МПа .

Напряжение изгиба

F = 2940 · 1,86 · 3,88/48 · 3,74 = 128,87 МПа < [ F] = 257,143 МПа .

Прочность на изгиб зубьев шестерни обеспечивается Проверка прочности зубьев при перегрузке:

по контактным напряжениям

Н max H TП /TН Н пр ,

по напряжениям изгиба

64

F max F TП /Т Н F пр.

Рабочее контактное напряжение

н 670Т1 Кн (u2 1) / d12 b u

670126 103 1,35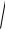3,152 1 / 85,772 48 3,15 476,317 МПа.

Предельные напряжения:

контактные

[ Н]пр = 3,1· Т = 3,1· 690 = 2139 МПа ;

изгиба

[ F]пр = 0,8 · Т = 0,8 · 690 = 552 МПа .

Поэтому

Нmax = 476,317 · 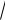1,8 = 339,046 МПа < [ Н]пр = 2139 МПа ;

Fmax = 128,87 ·1,8 = 231,966 МПа < [ F]пр= 552 МПа .

Прочность зубьев при кратковременных перегрузках обеспечивается. 6.3 Конструирование конических зубчатых колес

На рисунке 6.2 приведен чертеж конического колеса, который выполняют в следующей последовательности.

6.3.1 Устанавливают формат чертежа, определяют количество проекций и масштаб изображения конического колеса.

6.3.2 Изображают проекции. Колесо имеет цилиндрическую форму, для его изображения достаточно одной проекции. Но в отверстии колеса имеется шпо-

ночный паз. Для изображения ширины шпоночного паза на второй проекции изображают лишь отверстие со шпоночным пазом.

6.3.3 Выбирают базовую поверхность А − диаметр отверстия.

6.3.4 Выносят размеры колеса. Размерные линии располагают на расстоянии

8...10 мм от поверхности детали и между размерными линиями.

6.3.5 Проставляют шероховатости поверхностей. Базовое отверстия 30 и

профиль зубьев шлифуют с шероховатостью Ra1,25 , боковые грани шпоночно-

65

го паза и торцы зубчатого колеса обрабатывают с шероховатостями Rа2,5 , что достигают протягиванием и тонким точением. Поверхности детали, на которых

не указана обработка, имеют шероховатость Rz 63 изображенная в верхней части поля чертежа. Знак V показывает, что шероховатость на чертеже не ука-

зана.

6.3.6 Проставляют предельные отклонения размеров: базового отверстия

30Н7, ширины шпоночного паза 8Is9. Текстом на чертеже отмечены не

указанные предельные отклонения: валов h14, остальных ±Н14/2.

6.3.7 Указывают предельные отклонения формы и расположения поверхно-

0,05 А ( а – допуск отклонения размера отверстия 20Н7), допуск перпен-

дикулярности торцов.

6.3.8 Заполняют таблицу для изготовления и контроля конического зубчато-

го колеса:

внешний окружной модуль – me = 4 мм – линейная величина в раз меньшая шага, определяют по выражению (6.2);

число зубьев z – определяют передаточным числом механизма;

исходный контур – угол профиля исходного контура = 20 (угол зацепления);

коэффициент смещения Х. При нарезании зубчатых колес с z <17 происходит подрезание ножки зуба, уменьшается его прочность. Для предотвращения этого явления производят смещение режущего инструмента;

угол делительного конуса. Для зубчатого колеса tg 2 = и, для шестерни сtg 1 = и (u – передаточное число).

степень точности. Из 12 степеней точности для изготовления зубчатых колес наиболее распространены 6,7,8 и 9, 6 степень точности применяют при окруж-

ной скорости (15…30) м/с, 7 – (10…15) м/с, 8 – (6…10) м/с, 9 – (2…4) м/с;

межосевой угол передачи = 1 + 2;

внешний делительный диаметр, определяют из выражения (6.6);

66

обозначение чертежа сопряженного колеса – устанавливают из спецификации

сборочного чертежа механизма;

внешний диаметр вершин dае = dе + 2 mе · cos .

6.3.9Заполняют основную надпись чертежа.

6.3.10Отмечают на чертеже технические требования: твердость материала,

неуказанные предельные отклонения размеров.

7 Червячные передачи

7.1 Расчет червячных передач

7.1.1 Назначают исходные данные для расчета передачи: крутящие моменты

на червяке Т1 и червячном колесе Т2 , частоты вращения n1 и n2, передаточное число u, число заходов червяка z1 и число зубьев колеса z2, относительную толщину червяка q, характер нагрузки.

7.1.2 Из условия контактной прочности определяют межосевое расстояние

где – допускаемое напряжение на контактную прочность зубьев колеса,

зависящее от материала колеса и твердости червяка (таблица7.1);

K – коэффициент нагрузки:

K = K KV , (7.2)

K – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий, при постоянной нагрузке K = 1,0;

KV – коэффициент, учитывающий динамическую нагрузку, в зависимости от скорости и степени точности KV = 1,0…1,4.

7.1.3 Модуль зацепления

Полученное значение модуля округляют до стандартного значения в зави-

симости от q и и = z2/z1 (таблица 7.2).

67

68

Таблица 7.1 – Механические характеристики, допускаемые контактные напряжения [ н] и напряжения изгиба [ F] для материалов червячных колес,

МПа

Примечание. К – отливка в кокиль; П – отливка в песчаную форму; Ц – от-

ливка центробежная Таблица 7.2 - Параметры цилиндрических червячных передач (Гост 2144-76)

*Второй ряд

69

где ' – угол трения, в зависимости от скорости скольжения и материалов чер-

вяка и червячного колеса ' = (1,0…5,0) град.

7.1.6 Усилия в передаче:

окружное усилие на червяке

– угол профиля исходного контура, = 20 .

7.1.7Напряжение изгиба в зубьях червячного колеса

где K – коэффициент нагрузки, определяемый по (5.17);

YF – коэффициент формы зуба, выбирают из таблицы 5.2 по эквивалентно-

му числу зубьев:

F – допускаемые напряжения на изгиб (таблица 7. 1).

7.1.8 Проверка прочности зубьев колеса при кратковременных перегрузках производится по выражениям (5.20) и (5.21).

Для оловянных бронз [ ]Н пр = 4 Т , [ ]F пр = 0,8 Т ; для безоловянных бронз [ ]Н пр = 2 Т , [ ]F пр = 0,8 Т ; для чугуна [ ]Н пр = (260…300) МПа ,

[ ]F пр = 0,8 в .

70