18. Кинематика дифференциальных механизмов

Считая, что колеса 1 и 3 (см. рис. 28) вращаются независимо друг от друга и их угловые скорости известны, из (47) получим

_h = k₁₁ +k₃₃ , k₁ = - , k₃ = . (51)

По аналогии с (51) можно построить также зависимости ₁ = f (_h, ₃) и ₃ = f (_h, ₁).

Наиболее широкое распространение получили конические дифферен­циалы (см. рис. 28). Для их кинематического расчета воспользуемся методом остановленного водила. Основываясь на формуле (45), рассмотрим векторы

= - , = - , = - , = - = . (52)

В системе координат, жестко связанной с водилом ( , , - см. рис. 28), вектор = , а векторы абсолютных и относительных (по отношению к водилу) скоростей колес 1 и 3 направлены вдоль , так что, например, = ₁ , = и т. д. Здесь , ₁, и т. д. - алгебраические величины.

В силу (32) должно быть (см. рис. 28 ^ )

= , = . (53)

Из (53) имеем

= , = . (54)

Из рис. 29 видно, что

= + , = + . (55)

С учетом (55) из (54) получаем ^

y_p= x_p, y_Q = x_Q. (56)

Так как y_p = y_Q , x_p= - x_Q , то формулы (56) дают

=  , = -  ,  = .

Отсюда следует, что

+ = 0. (57)

Из (52) имеем

= - , = - . (58)

Подставляя (58) в (57), находим

= 0,5 ( + ), (59)

т. е. конический дифференциал обеспечивает алгебраическое суммирование величин и , причем в отличие от (51) коэффициенты при и равны друг другу.

19. Особенности проектирования планетарных передач

Основные геометрические параметры планетарных передач должны удовлетворять условиям соосности, сборки и соседства.

Условие соосности обеспечивает совпадение осей водила и центральных колес передачи с основной осью при отсутствии бокового зазора в зацепле­нии. Проиллюстрируем это условие на примере передачи по схеме на рис. 26.

Считая, что все колеса нарезаны несмещенным инструментом, получим, что теоретический боковой зазор будет равен нулю, если 0,5d₁+d₂= 0,5d₃, откуда с учетом (11):

z₁ + 2z₂ = z₃. (60)

Условие сборки требуется выполнять для того, чтобы оси сателлитов находились на одинаковых угловых расстояниях друг от друга. Можно показать, что для передачи по схеме на рис. 26 условие сборки имеет вид

= k, (61)

где n_с - число сателлитов, k - целое число.

Условие соседства состоит в том, чтобы окружности вершин соседних сателлитов не пересекались друг с другом. Если n_с  2, условие соседства выполняется автоматически.

20. Волновые зубчатые передачи

Схема волновой передачи показана на рис. 30. Здесь h - генератор волн, b и g - цилиндрические зубчатые колеса, соответственно жесткое и гибкое. Под действием генератора волн колесо g деформируется. При этом образуются симметрично расположенные зоны зацепления (см. рис. 30, а). В процессе вращения генератора волн зоны зацепления перемещаются, в том числе и по отношению к гибкому звену, в результате чего по гибкому колесу бежит волна деформации. Отсюда и название передачи - волновая.

Принцип действия передачи поясним с помощью рис. 31.

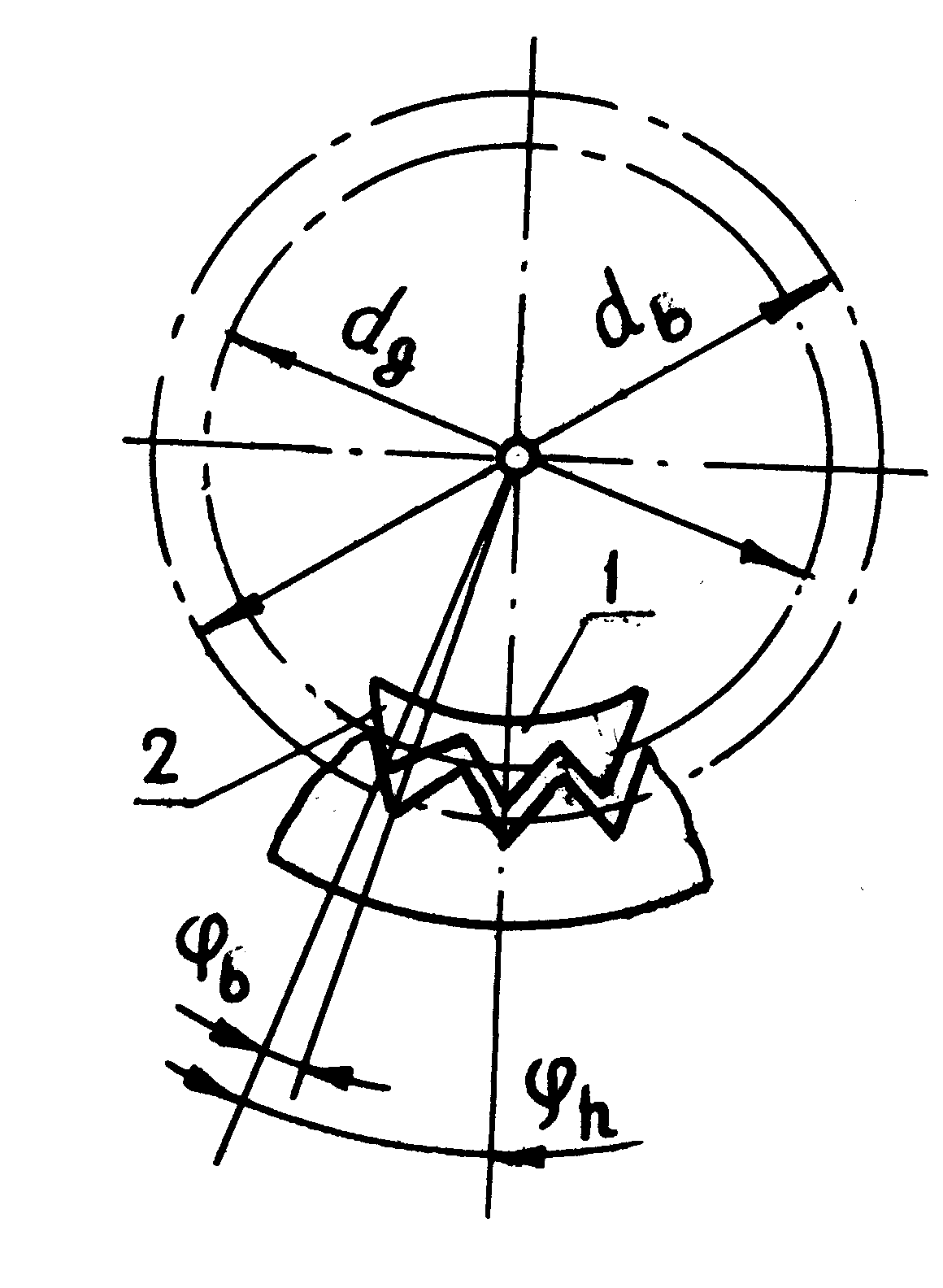
Рис. 30. Рис. 31.

Предварительно заметим, что угловые шаги _b и _g связаны с шагом зацепления p и делительными диаметрами d_b и d_g зависимостями

_b = , _g = , (62)

и так как (см. рис. 32) d_b > d_g , то

_b  _g . (63)

Кроме того, предположим, что колесо b может вращаться, а колесо g - нет.

Рассмотрим такое положение звеньев передачи, в котором ось симметрии зуба 1 (см. рис. 30, 31) совпадает с осью симметрии впадины между зубьями колеса b и c осью О₁О₂ генератора волн h. Очевидно, что в этом случае зуб 1 будет свободно входить во впадину. Повернем теперь генератор волн на угол

_h = _g . (64)

Деформируя колесо g, генератор волн тем самым будет стремиться ввести зуб 2 в соответствующую ему впадину, однако в силу неравенства (63) это будет возможно лишь в том случае, если колесо b повернется на угол (см. рис. 31)

_b = _g - _b . (65)

Таким образом, во-первых, приходим к выводу о том, что вращение генератора волн преобразуется во вращательное движение колеса b и, во-вторых, получаем формулу для определения передаточного отношения (см. (62) и (1)):

^ = = = = , (66)

где и - числа зубьев колес b и g.

Теперь будем считать неподвижным колесо b. Поворачивая генератор волн на угол _h = _b и замечая, что при этом гибкое колесо должно повернуться на угол

_g = - (_b - _g),

точно так же получим

= - . (67)

Основные достоинства волновых передач следующие.

1. Большие передаточные числа - до 300 в одной ступени (так как d_b и d_g близки друг к другу, то разность (z_b - z_g) по сравнению с z_b и z_g мала, и согласно (66) и (67)  1 и  1).

2. Возможность обеспечивать абсолютную герметизацию при передаче движения из одной среды в другую (рис. 30, б).

3. Высокая точность (вследствие большого числа одновременно зацеп­ляющихся зубьев и симметрии в расположении зон зацепления происходит взаимная компенсация погрешностей).

4. Плавность работы и малый шум (объясняется большим числом зацепляющихся зубьев и их постепенным входом в зацепление).

К числу недостатков волновых передач относятся следующие.

1. Сложность изготовления гибкого звена и повышенные требования к точности изготовления деталей.

2. Возможность “проскока” генератора волн при перегрузках.

3. Высокие значения минимально возможных величин передаточных чисел (> 60).