1.3 Система Mathcad. Аппроксимация. Функции аппроксимации. Решение дифференциальных уравнений

Система Mathcad

MathCAD является интегрированной системой программирования, ориентированной на проведение математических и инженерно-технических расчетов.

Система MathCAD содержит текстовый редактор, вычислитель и графический процессор.

Текстовый редактор – служит для ввода и редактирования текстов. Тексты являются комментарии и входящие в них математические выражения не выполняются. Текст может состоять из слов, математических выражений и формул, спецзнаков. Отличительная черта системы – использование общепринятой в математике символики (деление, умножение, квадратный корень).

Вычислитель – обеспечивает вычисление по сложным математических формулам, имеет большой набор встроенных математических функций, позволяет вычислять ряды, суммы, произведения, определенный интеграл, производные, работать с комплексными числами, решать линейные и нелинейные уравнения, проводить минимизацию функции, выполнять векторные и матричные операции и т.д. Легко можно менять разрядность чисел и погрешность интеграционных методов.

Графический процессор – служит для создания графиков. Он сочетает простоту общения с пользователем с большими возможностями графических средств. Графика ориентирована на решение типичных математических задач. Возможно быстрое изменение размеров графиков, наложение их на текстовые надписи и перемещение их в любое место документа. MathCAD автоматически поддерживает работу с математическим процессором. Последний заметно повышает скорость расчетов и вывода графиков, что существенно в связи с тем, что MathCAD всегда работает в графическом режиме. Это связано с тем, что только в этом режиме можно формировать на экране специальные математические символы и одновременно применять их вместе с графиками и текстом. MathCAD поддерживает работу со многими типами принтеров, а так же с плоттерами.

MathCAD – система универсальная, т.е. она может использоваться в любой области науки и техники, везде, где применяются математические методы. Запись команд в системе MathCAD на языке, очень близком к стандартному языку математических расчетов, упрощает постановку и решение задач.

Сегодня различные версии MathCAD являются математически ориентированными универсальными системами. Помимо собственно вычислений, как численных, так и аналитических, они позволяют с блеском решать сложные оформительские задачи, которые с трудом даются популярным текстовым редакторам или электронным таблицам.

С помощью MathCAD можно, например, готовить статьи, книги, диссертации, научные отчеты, дипломные и курсовые проекты не только с качественными текстами, но и с легко осуществляемым набором самых сложных математических формул, изысканным графическим представлением результатов вычислений и многочисленными «живыми» примерами. А применение библиотек и пакетов расширения обеспечивает профессиональную ориентацию MathCAD на любую область науки, техники и образования. [3]

Аппроксимация

Аппроксимацией называется нахождение такой функции f(x), которая была бы близка к заданной в соответствии с выбранным критерием. Задачей аппроксимации является нахождение функции f(x), проходящей через заданные узлы в соответствии с заданным критерием.

Аппроксимация заключается в том, что используя имеющуюся информацию по f(x) можно рассмотреть другую функцию ц(ч) близкую в некотором смысле к f(x), позволяющую выполнить над ней соответствующие операции и получить оценку погрешность такой замены.

Интерполяция (частный случай аппроксимации)

Если для табличной функции y=f(x), имеющей значение x₀ f(x₀) требуется построить аппроксимирующюю функцию j(x) совпадающую в узлах с x_i c заданной, то такой способ называется интерполяцией

При интерполяции, заданная функция f(x) очень часто аппроксимируется с помощью многочлена, имеющего общий вид

j(x)=p_n(x)=a_nxⁿ+a_n-1x^n-1+ … +a₀

В данном многочлене необходимо найти коэффициенты a_n,a_n-1, …a₀, так как задачей является интерполирование, то определение коэффициентов необходимо выполнить из условия равенства:

P_n(x_i)=y_i i=0,1,… n

Для определения коэффициентов применяют интерполяционные многочлены специального вида, к ним относится и полином Лагранжа L_n(x).

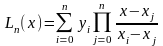i¹j

В точках отличных от узлов интерполяции полином Лагранжа в общем случае не совпадает с заданной функцией.

Функции аппроксимации

Для осуществления сплайновой аппроксимации MathCAD предлагает четыре встроенные функции. Три из них служат для получения векторов вторых производных сплайн-функций при различном виде интерполяции:

Cspine (VX, VY) – возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному;

pspline (VX, VY) – возвращает вектор \/S вторых производных при приближении к опорным точкам к параболической кривой;

Ispline (VX, VY) – возвращает вектор VS вторых производных при приближении к опорным точкам прямой.

Linterp (vs, vx, vy, х) – возвращает значение у(х) для заданных векторов VS, VХ, VУ и заданного значения х.

Таким образом, сплайн-аппроксимация проводится в два этапа. На первом с помощью одной из функций cspline, pspline или ispline отыскивается вектор вторых производных функции у(х), заданной векторами VХ и VУ ее значений (абсцисс и ординат). Затем на втором этапе для каждой искомой точки вычисляется значение у(х) с помощью функции interp. [5]

Решение дифференциальных уравнений

Для решения дифференциальных уравнений в MathCAD введен ряд функций. Остановимся на функциях, дающих решения для систем обыкновенных дифференциальных уравнений, представленных в обычной форме Коши:

• rkadapt (y, x1, x2, acc, n, F, k, s) – возвращает матрицу, содержащую таблицу значений решения задачи Коши на интервале от х1 до х2 для системы обыкновенных дифференциальных уравнений, вычисленную методом Рунге-Кутта с переменным шагом и начальными условиями в векторе у (правые части системы записаны в векторе F, n – число шагов, k – максимальное число промежуточных точек решения, и s – минимально допустимый интервал между точками);

• Rkadapt (y, x1, x2, n, F) – возвращает матрицу решений методом Рунге-Кутта с переменным шагом для системы обыкновенных дифференциальных уравнений с начальным условием в векторе у, правые части которых записаны в символьном векторе F на интервале от х1 до х2 при фиксированном числе шагов n;

• rkfixed (y, x1, x2, n, F) – возвращает матрицу решений методом Рунге-Кутта системы обыкновенных дифференциальных уравнений с начальным условием в векторе у, правые части которых записаны в символьном векторе F на интервале от х1 до х2 при фиксированном числе шагов n.

В данной курсовой работе для решения дифференциального уравнения применена функция rkfixed (см. приложение) которая использует для поиска решения метод Рунге-Кутта четвертого порядка. В результате решения дифференциального уравнения первого порядка получается матрица, имеющая два столбца:

– первый столбец содержит значение точек, в которых ищется решение дифференциального уравнения;

– второй столбец содержит значения найденного решения в соответствующих точках.

Функция rkfixed (y, x1, x2, npoints, D) имеет следующие аргументы:

у – вектор начальных условий размерности n, где n – порядок дифференциального уравнения или число уравнений в системе дифференциальных уравнений, для уравнения первого порядка вектор начальных условий вырождается в одну точку;

х1, х2 – граничные точки интервала, на котором ищется решение дифференциальных уравнений;

npoints – число точек (не считая начальной точки), в которых ищется приближенное решение;

D (x, y) – функция, возвращающая значение в виде вектора из п элементов, содержащих первые производные неизвестных функций.

Решение дифференциального уравнения второго порядка

Основные отличия решения уравнений второго порядка в MathCAD от решения уравнения первого порядка состоят в следующем:

– вектор начальных условий состоит из двух элементов: значений функции и ее первой производной в начальной точке интервала;

– функция D (x, y) является вектором с двумя элементами:

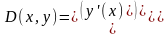
– матрица, полученная в результате решения, содержит три столбца: первый столбец содержит значения х, второй – у(х), третий – у’ (х).

Решение дифференциального уравнения n-го порядка

Методика решения дифференциальных уравнений более высокого порядка является развитием методики, примененной для решения уравнения второго порядка. Основные различия состоят в следующем:

– вектор начальных условий состоит из п элементов: значений функции и ее производных: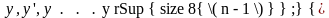

– функция D является вектором, содержащим п элементов:

– матрица, полученная в результате решения, содержит п столбцов: первый столбец содержит значения х, оставшиеся столбцы содержат значения .
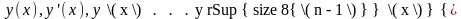