2.1.4. Проверочный расчет по напряжениям изгиба

Расчет производится в следующей последовательности.

1. Определяют окружную силу

, Н.

2) Определяют коэффициент нагрузки

_.

Здесь – коэффициент концентрации нагрузки (таблица 2.10); – коэффициент динамичности (таблица 2.11).

3) Определяют для шестерни и колеса отношение , где Y_F – коэффициент, учитывающий форму зуба (таблица 2.12).

Таблица 2.10

Значение коэффициента при твердости рабочих поверхностей зубьев HB ≤ 350

	Расположение зубчатых колес по отношению к опорам
	симметричное	несимметричное	консольное
0,2	1,00	1,04	1,18
0,4	1,03	1,07	1,37
0,6	1,05	1,12	1,62
0,8	1,08	1,17	–
1,0	1,10	1,23	–
1,2	1,13	1,30	–
1,4	1,19	1,38	–
1,6	1,25	1,45	–
1,8	1,32	1,53	–

Таблица 2.11

Значение коэффициента при твердости рабочих поверхностей зубьев HB ≤ 350

Степень точности	Окружная скорость v, м/с
	3	3…8	8…12,5
6	1,00/1,00	1,20/1,00	1,30/1,10
7	1,15/1,00	1,35/1,00	1,45/1,20
8	1,25/1,10	1,45/1,30	–/1,40
Примечание: в числителе указаны значения KFv для прямозубых передач, в знаменателе – для косозубых

Таблица 2.12

Значения коэффициента Y_F по ГОСТ 21354–75

Число зубьев z	17	20	25	30	40	50	60	70	80	100
YF	4,28	4,09	3,90	3,80	3,70	3,66	3,63	3,62	3,61	3,60

Для косозубых колес коэффициент Y_F следует выбирать по эквива­лентному числу зубьев

.

Далее расчет следует вести для зубьев того из колес, для которого меньше.

4) Определяют расчетное значение напряжения изгиба и сравнивают с допускаемым:

а) для прямозубых колес

;

б) для косозубых колес

.

Здесь – поправочный коэффициент; – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями (при учебном проектировании можно принять = 0,92); b – ширина венца зубчатого колеса, мм; m_n – модуль зацепления, мм.

2.2. Пример расчета цилиндрической зубчатой передачи

Рассчитать одноступенчатую цилиндрическую косозубую передачу по следующим данным: крутящие моменты на валах Т₁ = 35 Hм, Т₂ = 170 Hм; передаточное число u = 5; угловая скорость ведущего вала ₁ = 151,77 рад/с.

Для зубчатой передачи марки сталей шестерни и колеса выбираем одинаковые. Для передачи с косыми зубьями выбираем сталь марки 40Х с улучшением, с твердостью: для колеса НВ250, для шестерни НВ270.

Допускаемые контактные напряжения, МПа:

,

где – предел контактной выносливости при базовом числе циклов, – коэффициент долговечности, для длительной эксплуатации ; – коэффициент безопасности, примем = 1,1.

Определим значения:

МПа;

МПа.

Тогда

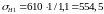МПа;

МПа.

Общее допускаемое контактное напряжение равно:

МПа.

Условие

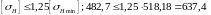МПа выполняется.

При твердости зубьев HB ≤ 350 принимаем = 1,8 HB, = 1,75, К_FL = 1. Для шестерни 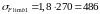МПа, для колеса МПа.

Соответственно, допускаемое напряжение на выносливость при изгибе для шестерни МПа, для колеса МПа.

Проектный расчет зубчатой передачи

Межосевое расстояние определяем по формуле:

Здесь = 43 – вспомогательный коэффициент для косозубых передач; Т₂ = 17010³ Нмм – крутящий момент на валу зубчатого колеса, задан по условию; K_нβ = 1 – коэффициент нагрузки (таблица 2.2); = 482,7 МПа – допускаемое контактное напряжение; u = 5 – передаточное число; Ψ_ba = 0,25 – коэффициент ширины венца.

Округляем до ближайшего значения a_w = 125 мм.

Определяем значение модуля: m_n = (0,01…0,02) a_w = 0,016∙125 = 2, выбираем стандартное значение модуля m_n = 2.

Принимаем предварительно угол наклона .

Проверяем выполнение условия:

; ;

условие выполняется.

Определяем общее число зубьев шестерни и колеса:

;

;

.

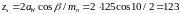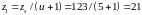Уточняем фактическое передаточное число:

; несоответствие заданному составит Δ = (u – u_ф.) / u_ф100 = (5 – 4,86) / 5 ∙ 100 = 2,8 %  4 %, условие выполняется.

Уточняем величину угла наклона линии зуба

.

Рассчитываем геометрические параметры зубчатых колес (таблица 2.13).

По ГОСТ 2.403–75 уточняем ширину венца: b₁ = 42 мм; b₂ = 32 мм.

Таблица 2.13

Геометрические параметры зубчатой передачи

Параметры	Шестерня	Колесо
Делительный диаметр, мм
Диаметр окружности вершин зубьев, мм
Диаметр окружности впадин зубьев, мм
Ширина венца, мм
Высота зуба, мм
Высота головки зуба, мм
Высота ножки зуба, мм

Проверочный расчет по контактным напряжениям

Определяем коэффициент ширины шестерни

.

Определяем окружную скорость колёс, м/c²

.

Выбираем 8–ую степень точности.

Определяем коэффициент нагрузки

.

Коэффициенты , , определяем соответственно по таблицам 2.7, 2.8 и 2.9: ; ; .

Тогда .

Определяем фактическое контактное напряжение , МПа, и сравниваем его с допустимым:

;

–

условие выполняется.

Определяем величину недогрузки передачи:

%,

что соответствует требованию менее 10 %.

_{Проверочный расчет по напряжениям изгиба}

_{Проверку зубьев зубчатого колеса на выносливость при изгибе выполняем согласно формуле:}

.

Определяем значение окружной силы:

Н,

Н.

Определяем коэффициент нагрузки:

;

где = 1,1– коэффициент концентрации нагрузки (таблица 2.10); = 1,2– коэффициент динамичности (таблица 2.11).

Определяем значение Y_F: при ; по таблице 2.12 Y_F1 = 4,052.

;

соответственно Y_F2 = 3,6.

Определяем отношение :

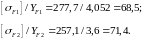
Расчет производим для наименьшего отношения.

Тогда:

МПа.

Условие выполняется, следовательно, проектирование зубчатой передачи выполнено верно.