256

Рисунок 5.43

5.2.11.2. Порядок расчета пружин сжатия и растяжения

На винтовые цилиндрические пружины сжатия и растяжения из стали круглого сечения имеются ГОСТы, в которых регламентируются и рекоменду-

ются к использованию в расчетах максимальные касательные напряжения τ3

при действии максимальной силы F3. Отметим, что такие пружины работают в основном на кручение.

Расчет проиллюстрируем на примере стальной пружины сжатия. Для пружин растяжения расчет аналогичен.

Исходные данные: сила пружины при предварительном перемещении F1 и рабочем перемещении F2 . Рабочий ход h.

Решение. 1. Определяется величина силы F3 пружины при максимальной деформации F3 = k1 F2 (k1 =1,15...1,3).

2.Для выбранного материала находится максимальное касательное напряжение τ3 .

3.Задается индекс пружины i = D / d . Рекомендуются следующие индексы i в зависимости от диаметра проволоки:

Поскольку расчет ведется по максимальной нагрузке, то используется максимальная сила и максимальные напряжения. Полученное значение округляется до значения диаметра d, соответствующего сортаменту.

6.Определяется средний диаметр пружины D = d i .

7.Необходимое число витков n для обеспечения рабочего перемещения

пружины s2 n = G d 4 / (8 D3 c)= G d / (8 c i3 ), где с – жесткость пружины.

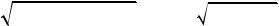
257

Тарельчатыепружиныпредназначеныдлявосприятиябольшихсжимающих сил при малых перемещениях. Эти пружины изготавливаются в виде тарелок без днищ из стали марки 60С2А, твердость материала 45,5...51,5 HRCЭ

(рис. 5.44, а, где D , D1 – наружный и внутренний диаметры пружины). Тарельчатые пружины располагаются в комплекте из нескольких штук (см. табл. 5.6). Рабочая деформация пружины s =0,8 f3 .

Пружины кручения. К ним относятся витые, плоские спиральные пружины и торсионы. При использовании пружин кручения нужно учитывать то, что плоские спиральные пружины имеют меньшие габариты и большую податливость, чем витые цилиндрические, но выдерживают меньшие крутящие моменты. Торсионы имеют малые радиальные размеры, но большую длину и воспринимают значительные крутящие моменты при небольшой податливости

(рис. 5.44, б, где 3 – законцовка). Витые цилиндрические пружины кручения навиваются из проволоки круглого сечения с зазором 0,2...0,5 мм между витками, во избежание трения между ними. Примеры оформления концов пружины для восприятия крутящего момента приведены на рис. 5.43, б. При установке пружина должна центрироваться. Кроме того, диаметр центрирующего элемента должен выбираться так, чтобы при скручивании пружины, когда ее диаметр уменьшается, между витками пружины и центрирующей поверхностью оставался зазор. При действии крутящего момента основная нагрузка на виток связана с его изгибом.

5.2.11.3. Порядокрасчетавитойцилиндрическойпружиныкручения

Исходные данные: вращающий момент пружины при предварительном

σ3 =(0,4...0,6) σВ (большее значение при меньшем числе циклов нагружения).

3.Определяется диаметр проволоки пружины при нагрузке T3 :

d* = 332 T3 k / (π σ3 ) = 2,16 3T3 k /σ3

258

щим моментом Ti ϕi =Ti /c .

Плоские спиральные пружины (см. табл. 5.6) изготавливаются из тонкой высококачественной углеродистой стальной ленты. Они применяются в качестве пружинных двигателей, аккумулирующих энергию при заводе. Благодаря высокой гибкости ленты пружина аккумулирует значительное количество энергии и позволяет осуществить угол поворота валика до нескольких десятков оборотов.

Рисунок 5.44

Торсион представляет собой цилиндрический стержень с законцовками 3 на торцах для его крепления (рис. 5.44, б). Обычно заделка осуществляется с помощью эвольвентного шлицевого соединения. Использование торсионов особенно целесообразно в случае соединения полых соосных деталей, когда конструкция позволяет использовать торсионы значительной длины. В этих случаях угол закручивания может достигать нескольких десятков градусов.

259

Для снижения массы торсионы часто делаются полыми. Эффективно изготавливать торсионы из титановых сплавов, что не только снижает массу, но и благодаря меньшему модулю упругости, чем у стали, обеспечивает больший угол поворота.

5.3. ВВЕДЕНИЕ В ТЕОРИЮ ВЫСШЕЙ ПАРЫ

В разделе 2 рассматривались задачи анализа и синтеза технических систем с низшими кинематическими парами. Низшие пары обеспечивают передачу значительных силовых факторов. Однако реализация структур технических систем только низшими парами не всегда целесообразна из-за сложности кинематической схемы. В таких случаях используют механизмы с высшими кинематическими парами, которые позволяют воспроизвести практически любой закон движения при минимальном числе звеньев. Наличие высшей кинематическойпарыпозволяетсократить число подвижныхзвеньев,чтоприводит к уменьшению габаритов механизма. Типовой механизм с высшей кинематическойпаройсостоитизстойкиидвухподвижныхзвеньев.Подвижныезвенья, взаимодействуя со стойкой, образуют низшие кинематические пары, а между собой составляют высшую кинематическую пару.

5.3.1. Теорема о высшей кинематической паре

Поверхности звеньев, образующих высшую кинематическую пару и обеспечивающие заданные законы их относительного движения, называются

сопряженными или начальными.

В теории зубчатых механизмов сделанный вывод носит название основной теоремой зацепления, которая доказана Виллисом. Основная теорема зацепления рассматривает отношение угловых скоростей звеньев, которое называется кинематическим передаточным отношением:

i12 = ω1 .

ω2

Полученное выражение определяет основное свойство теоремы зацепления, которая имеет следующую формулировку: передаточное отношение звеньев, совершающих вращательные движения прямо пропорционально отношениюугловыхскоростейиобратнопропорциональноотношениюрасстоянийот центров вращения до полюса.

5.3.2. Механизмы с высшими кинематическими парами

260

Механизм с высшей кинематической парой − это механизм, структура которого содержит хотя бы одну высшую кинематическую пару.

К типовым механизмам данного вида относятся:

−механизмы фрикционные (рис. 5.46, 5.47);

−механизмы с гибкими звеньями (рис. 5.48, 5.49);

−механизмы мальтийские (рис. 5.50, а);

−механизмы поводковые (рис. 5.50, б);

−механизмы зубчатые (рис. 5.51, 5.55, 5.56, 5.57);

−механизмы цевочные (рис. 5.53.)

Фрикционный механизм − это механизм с высшей кинематической парой, в котором передача движения и преобразование силовых факторов осуществляется за счет сил трения или сцепления.

Фрикционные механизмы обладают рядом достоинств: простота конструкции, бесшумность работы, предохранение от перегрузок, возможность бесступенчатого изменения передаточного отношения, что подтверждается их применением практически в машинах всех видов.

Все фрикционные механизмы делятся на две группы: типовые (простые) механизмы (рис. 5.46) и вариаторы (рис. 5.47).

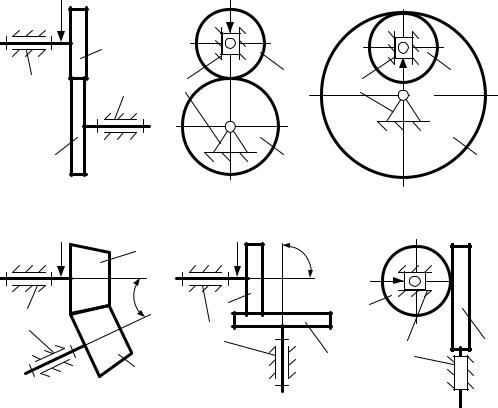
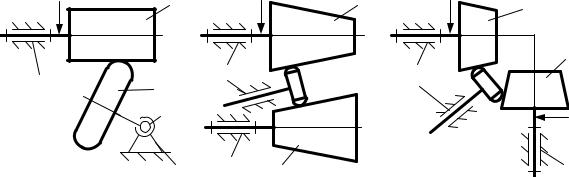
Схема типового фрикционного механизма содержит: стойку и два подвижных звена, которыми являются катки 1 и 2 (рис. 5.46, а – г), каток 1 и диск 2 (рис. 5.46, д) и каток 1 и плоскость 2 (рис. 5.46, е).

261

Рисунок 5.46 – Структурные схемы фрикционных механизмов

Простые фрикционные механизмы подразделяются на следующие группы: механизмы с параллельными осями и механизмы с пересекающимися осями. К простым фрикционным механизмам относятся цилиндрические с внешним (рис. 5.46, а, б) или внутренним касанием (рис. 5.46, в), а механизмами с пересекающимися осями являются конические (рис. 5.46, г) и лобовые (рис. 5.46, д). Лобовыми называются конические фрикционные механизмы, имеющие значение угла пересечения осей подвижных

звеньев δ =900 .

Во фрикционных механизмах преобразование движения и силовых факторов осуществляется путем непосредственного касания рабочих поверхностей подвижных звеньев. Однако для создания достаточной по

их повышенный износ. Непостоянство передаточного отношения существенно сужает область применения данных механизмов.

Фрикционные механизмы, обладающие возможностью изменения передаточногоотношениявзаданномдиапазоне,называютсявариаторы(рис. 5.47). Вариаторы применяются в машинах разного назначения, требующих плавного

Рисунок 5.47 – Структурные схемы фрикционных вариаторов

Вариаторы делятся на две группы:

− вариаторы с непосредственным касанием звеньев – это вариаторы,

в которых регулирование значений передаточной функции (передаточного отношения) осуществляется за счет перемещения одного из звеньев-катков

(рис. 5.47, а).

262

− вариаторы с промежуточным звеном звеньев – это вариаторы,

в которых регулирование значений передаточной функции (передаточного отношения) осуществляется за счет перемещения промежуточного звена

(рис. 5.47, б, в).

Передаточная функция (передаточное отношение) вариаторов бесступенчато изменяется в пределах от 2,5 до 5.

Механизмы с гибкими звеньями – это механизмы с высшими кинемати-

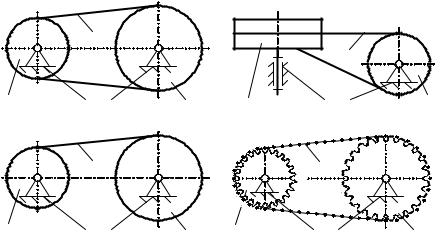
и три подвижных звена, которыми являются гибкое звено 3 и шкивы 1 и 2 (рис. 5.48, а, б) или валки 1 и 2 (рис. 5.48, в) или звездочки 1 и 2 (рис. 5.48, г). В качестве гибких звеньев выступают: ремни, шнуры, канаты, тросы проволока, ленты, цепи и др. Механизмы c гибкими звеньями обладают рядом существенных достоинств: простота конструкции, плавность работы, возможность передачи движения на большие расстояния при малом числе звеньев, что подтверждается их применением практически в машинах всех видов, а также в приборостроении.Механизмыc гибкимизвеньямиподразделяютсямеханизмы

и механизмы с зацеплением – цепные (рис. 5.48, г). Ременные механизмы и механизмы с непосредственным креплением подразделяются на механизмы с параллельными осями или открытые (рис. 5.48, а, в), механизмы перекрестные и механизмы со скрещивающимися осями или полуперекрестные (рис. 5.48, б). Цепные механизмы бывают только открытыми (рис. 5.48, г).

и силовых факторов осуществляется посредствам изменения формы рабочих

263

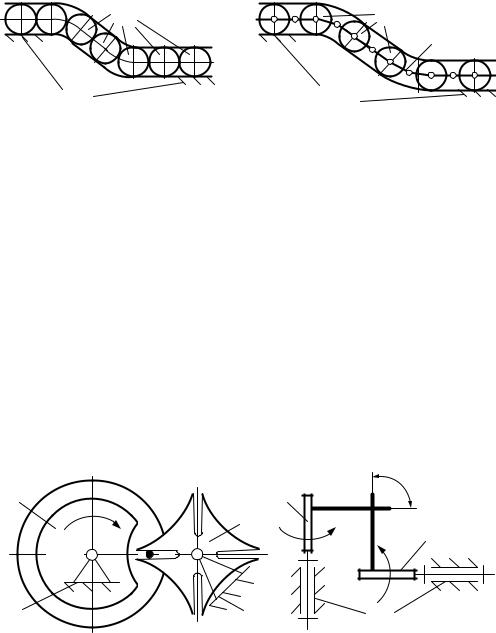
поверхностей гибкого звена. Наличие проскальзывания и вытягивания ремней, канатов и тросов в ременных механизмах и механизмах с непосредственным креплением,повышенный износ цепей в цепных механизмах, а также непостоянство передаточного отношения всех видов механизмов данного вида существенно сужает область их применения. Частным случаем механизмов с гибкими звеньями являются шариковые механизмы, образованные гибким шлангом и набором шариков (рис. 5.49).

Рисунок 5.49 – Структурные схемы шариковых механизмов

В типовых схемах шариковых механизмов гибкий шланг является элементом стойки 0, а в качестве подвижных звеньев выступают шарики 1. Наличие гибкого шланга в шариковых механизмах обеспечивает возможность преобразования движения и силовых факторов на большие расстояния при произвольномрасположенииосейиминимальномчислезвеньев,чтообеспечивается непосредственным касанием шариков друг с другом (рис. 5.49, а). С целью исключения контакта шариков 1 между собой в механизмах данного вида применяется гибкий сепаратор 2 (рис. 5.49, б), что значительно снижает износ рабочих поверхностей звеньев, повышая долговечность и ресурс работы механизма.

Мальтийский механизм – это механизм, содержащий кривошип, имеющий специальный выступ-палец прерывисто сцепляющийся с пазом выходного звена (рис. 5.50, а).

Рисунок 5.50 – Схемы мальтийского и поводкового механизмов