2.2 Построение механизма.

На листе вычерчиваем схему механизма, выбрав масштаб построения,

_l =500 мм/м

Тогда АО = 50 мм; АВ  200 мм; АS₂ = 76 мм.

2.3 Нахождение скоростей точек механизма.

Рассматриваем звено 1: V_A = ₁∙L_OA = 52,2 ∙ 0,1 = 5,22 м/с

Рассматриваем звенья 2-3:

Строим план скоростей в масштабе _V = 20

||Oy OA AB

Из построения находим:

Точка S₂ лежит на звене 2 и делит её в той же пропорции, что и на плане скоростей. Т.е. можно составить отношение и отсюда найти положение точки S₂ на плане скоростей.

Находим скорость центра масс звена 2.

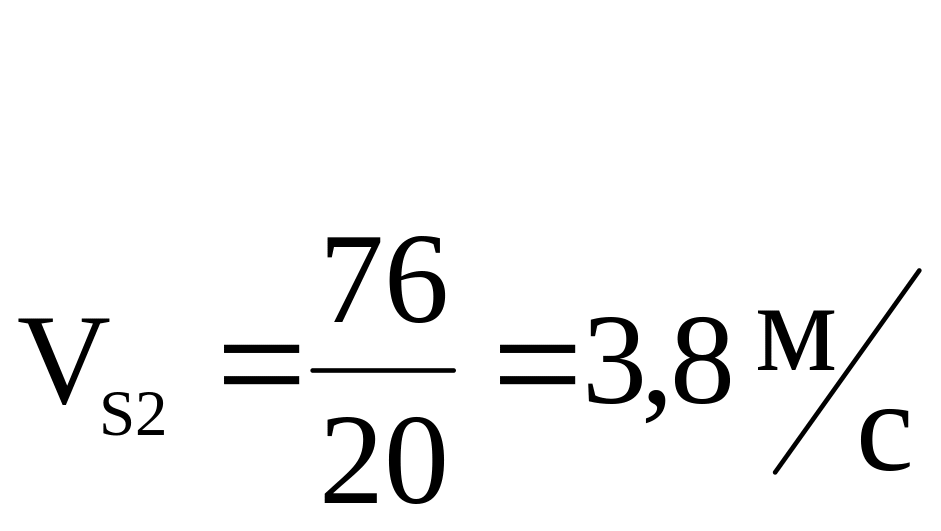
Определим угловую скорость звена 2:

2.4 Определение ускорений точек механизма.

Звено 1:

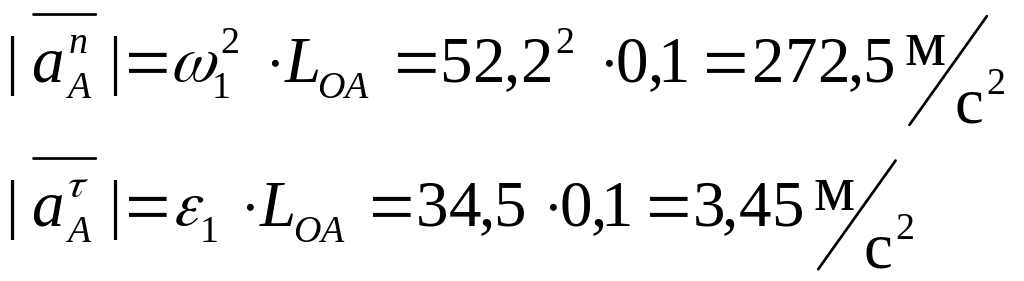
Составляем векторное уравнение:

т.к. траекторией точки В является прямая, то нормальная составляющая ускорения равна 0, тогда:

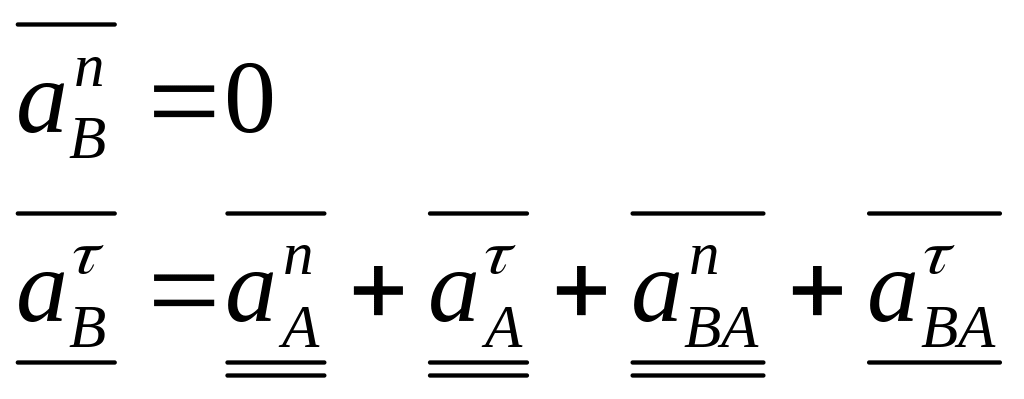
м/с²

||Ox ||OA OA ||AB AB

Определяем нормальную составляющую ускорения звена 2:

м/с²

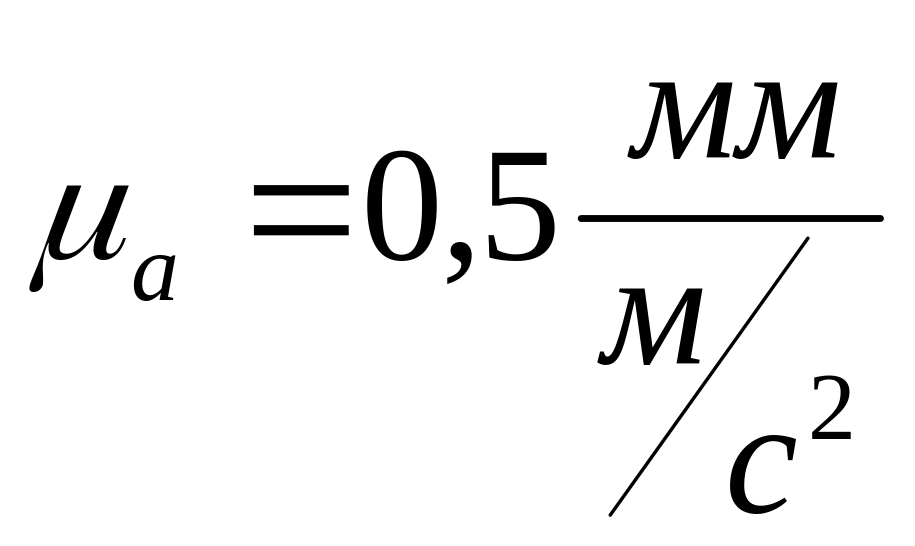
Будем строить план ускорений в масштабе:

мм мм

мм

Из плана ускорений определяем:

мм мм мм

Тогда действительные величины ускорений будут пересчитываться по формуле:

с учётом этой формулы:

Определим ускорение точки S₂.

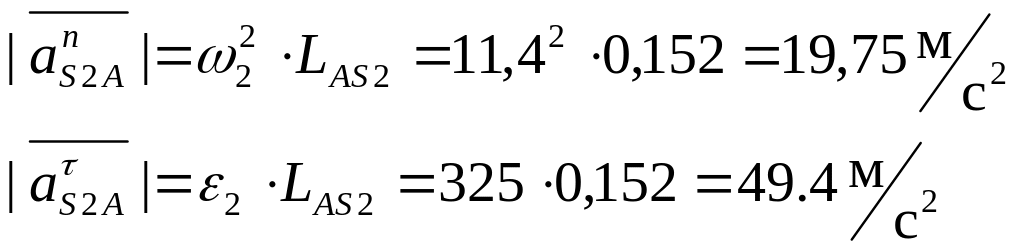
2.5 Определение значений и направлений главных векторов и главных моментов сил инерции для заданного положения механизма.

Необходимые для расчётов величины:

m₂=14 кг m₃=23 кг I_S2=0,067 кг∙м∙с² = 0,67 кг∙м²

1). Определяем силы инерции:

Ф_S1=0 , т.к. центр масс 1-го звена неподвижен.

Знак минус в формуле указывает на то, что вектор силы инерции направлен в сторону, противоположную соответствующему ускорению.

2). Определяем моменты сил инерции:

М_ф1 = −₁ ∙ I_S1 => М_ф1 = 34,5 ∙ 188 = 6486 Н∙м

М_ф2 = −₂ ∙ I_S2 => М_ф2 = 325 ∙ 0,67 = 217,75 Н∙м

Знак минус в формуле указывает на то, что моменты сил инерции направлены в сторону, противоположную соответствующему угловому ускорению.

2.6 Силовой расчёт.

Силовой расчет проводится по графоаналитическому способу (при решении используют алгебраические уравнения моментов сил и векторные уравнения для сил, приложенных к звеньям механизма). Механизм при силовом расчете расчленяют на статически определимые группы звеньев (группы Ассура).

Задачу решаем с того звена, к которому приложена известная сила. В нашем случае это звено 3, и сила, приложенная к звену – это движущая сила F = 118 кH.

1) Рассмотрим звено 2:

записываем уравнение моментов относительно точки В:

(*)

Строим изображения звеньев 2 и 3 в масштабе _L=500 мм/м

и, измеряя плечи сил Ф_S2 и G₂, получаем соответственно:

Z_hG2 = 16 мм и Z_hФs2 = 56 мм

из соотношения (*) определяем значение реакции

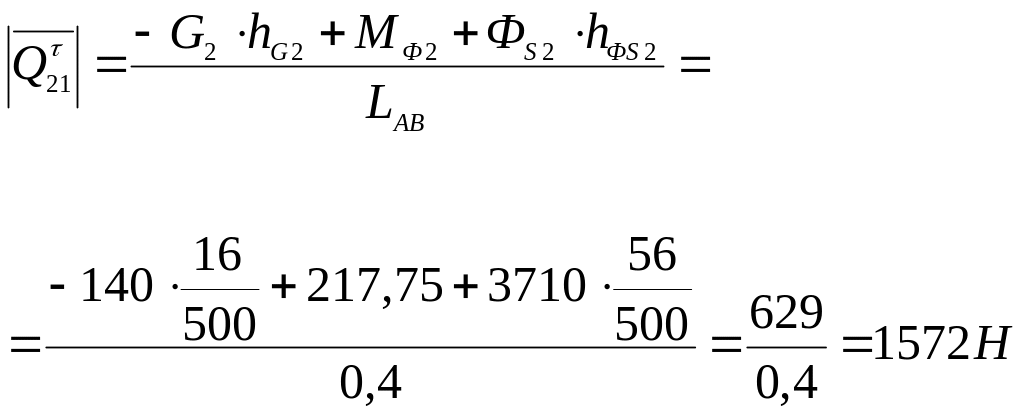
2)Рассмотрим звенья 2 и 3 совместно.

Рассматриваем двухповодковую группу Ассура и записываем для неё уравнение равновесия (уравнение Даламбера):

решаем это уравнение строя план сил в масштабе _F =0,003 мм/H

и з плана находим:

3) Рассмотрим звено 3.

Записываем уравнение Даламбера для этого звена:

р ешаем это уравнение, строя план сил в масштабе _F =0,003 мм/H.

Из плана, измеряя величину отрезка, характеризующего реакцию Q₃₂ ,получаем:

4) Рассмотрим звено 1.

Изображаем звено 1 в масштабе _L =500 мм/м.

Запишем сумму моментов относительно точки О:

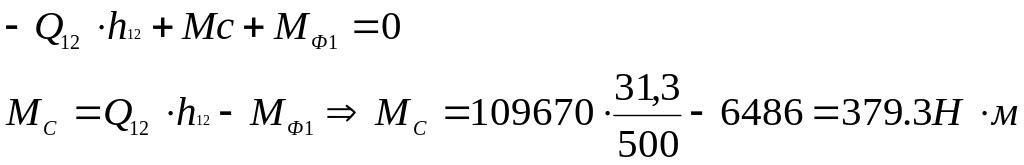
тогда погрешность по сравнению с величиной момента, полученной на первом листе, составит: