
- •Техническое задание
- •1. Проектирование основного механизма и определение закона движения механизма
- •1.1 Определение размеров механизма.
- •Максимальное давление в цилиндре двигателя
- •1.3 Построение графика силы f
- •1.4 Построение планов возможных скоростей.
- •Проведя аналитическое интегрирование графика (1), получим кривую работы приведенного момента движущих сил.
- •Данные приведены в таблице 1.6.
- •1.7 Построение графика суммарной работы .
- •1.8 Построение графиков приведенных моментов инерции звеньев II группы.
- •1.11 Определение необходимого момента инерции первой группы звеньев .
- •1.14 Построение графика (приближенного) угловой скорости .
- •2.Силовой расчёт механизма
- •2.1 Начальные данные.
- •2.2 Построение механизма.
- •2.3 Нахождение скоростей точек механизма.
- •2.4 Определение ускорений точек механизма.
- •2.5 Определение значений и направлений главных векторов и главных моментов сил инерции для заданного положения механизма.
- •2.6 Силовой расчёт.
- •3. Проектирование кулачкового механизма.
- •3.1 Исходные данные для проектирования.
- •3.2. Построение кинематических диаграмм методом графического интегрирования.
- •3.3. Определение основных параметров кулачкового механизма графическим способом.
- •3.4 Построение профиля кулачка.
- •3.5 Построение графика изменения угла давления.
- •Третий лист проекта
- •3. Проектирование зубчатой передачи и планетарного механизма.
- •3.1 Выбор коэффициентов смещения.
- •3.2. Построение профиля зуба, изготовляемого реечным инструментом.
- •3.2. Построение проектируемой зубчатой передачи.
- •3.3. Проектирование планетарного зубчатого механизма с цилиндричискими колесами.
- •3.4. Проверка графическим способом правильности передаточного отношения планетарного редуктора.
- •Приложение 3. Расчет зубчатой передачи.
3.2. Построение проектируемой зубчатой передачи.
Проектируемая зубчатая передача строится следующим способом:
(все данные необходимые для построения берутся из программы Mzub)
Откладываем межосевое расстояние
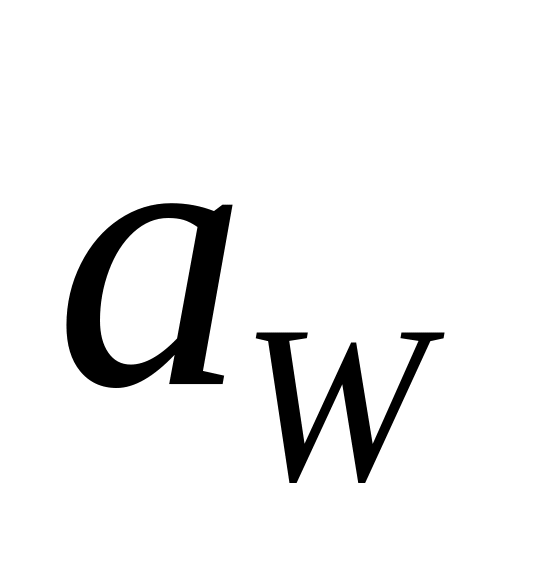 и
проводим окружности: начальные
и
проводим окружности: начальные
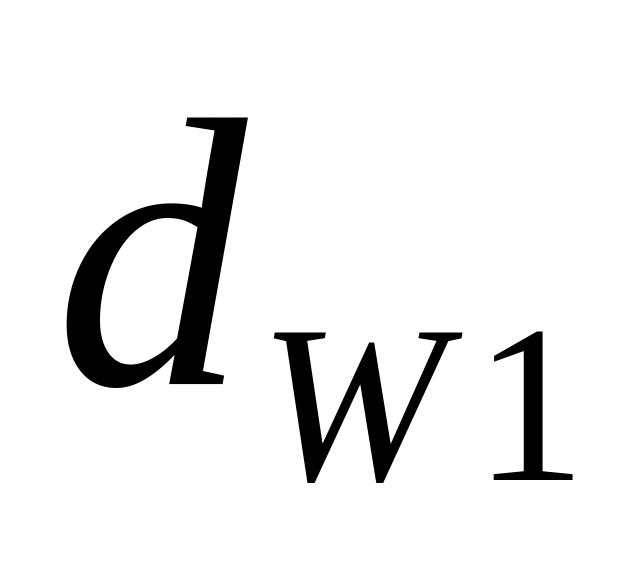 и
и
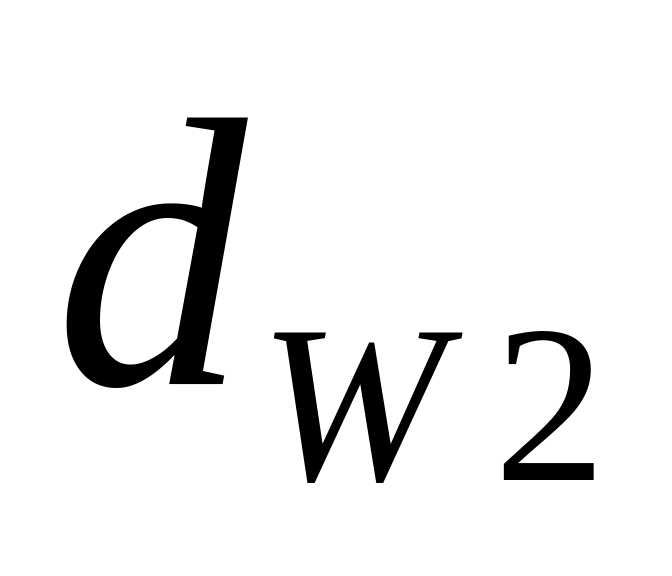 ;
делительные
;
делительные
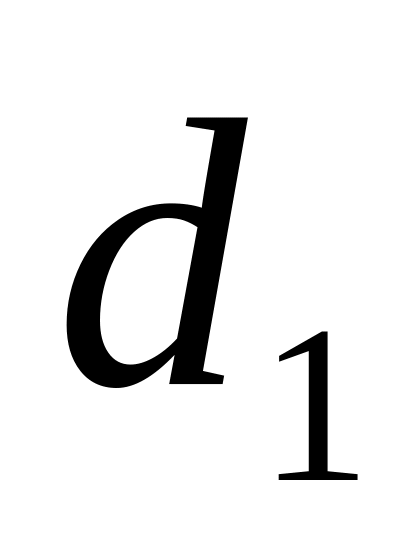 и
и
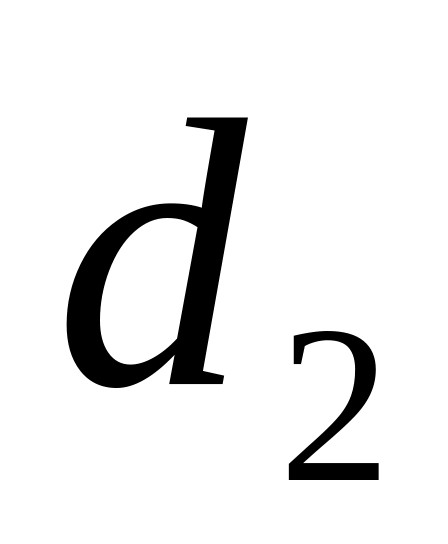 и
основные
и
основные
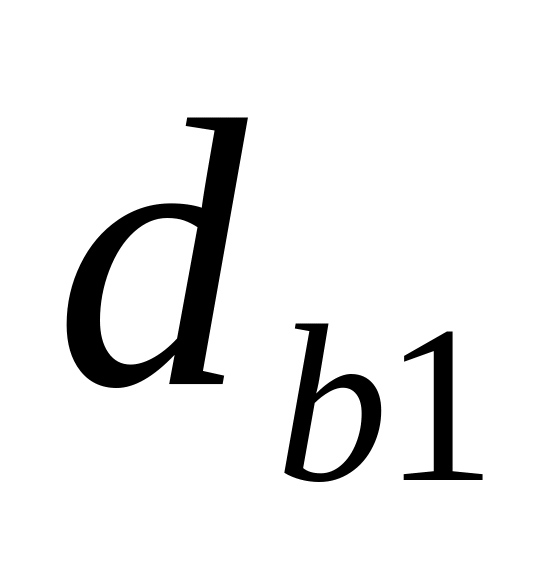 и
и
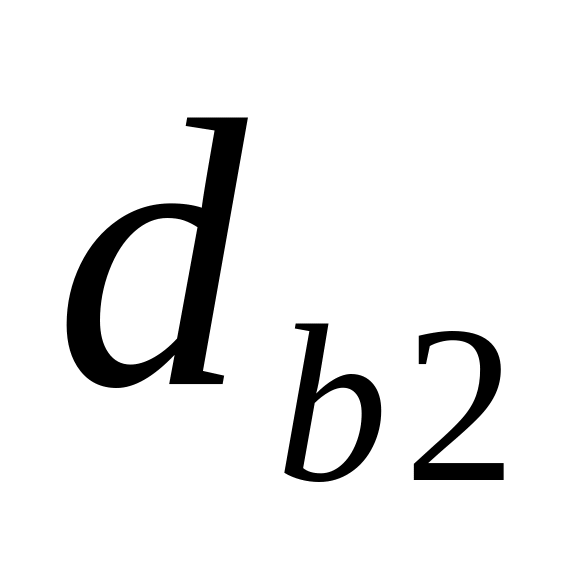 ;
окружности вершин
;
окружности вершин
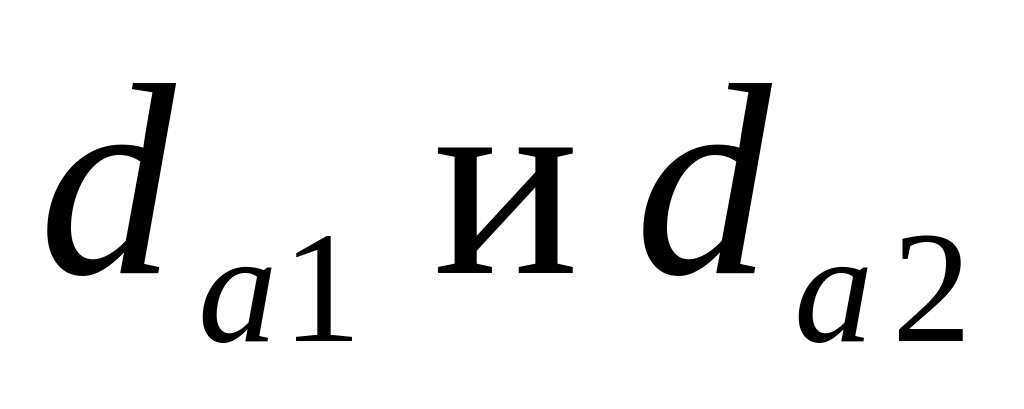 и впадин
и впадин
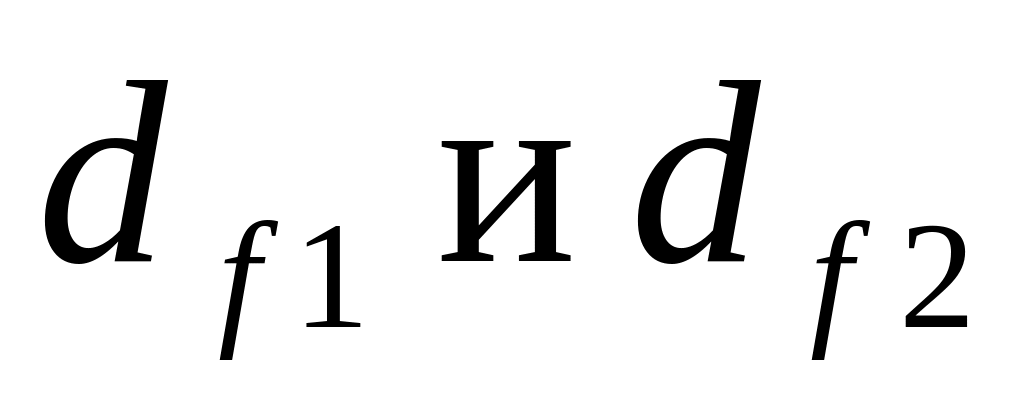 .
Начальные окружности касаются в полюсе
зацепления. Расстояние между делительными
окружностями по осевой линии равно
воспринимаемому смещению
.
Начальные окружности касаются в полюсе
зацепления. Расстояние между делительными
окружностями по осевой линии равно
воспринимаемому смещению
 .
Расстояние между окружностями вершин
одного колеса и впадин другого,
измеренного по осевой линии, должно
быть равно радиальному зазору
.
Расстояние между окружностями вершин
одного колеса и впадин другого,
измеренного по осевой линии, должно
быть равно радиальному зазору
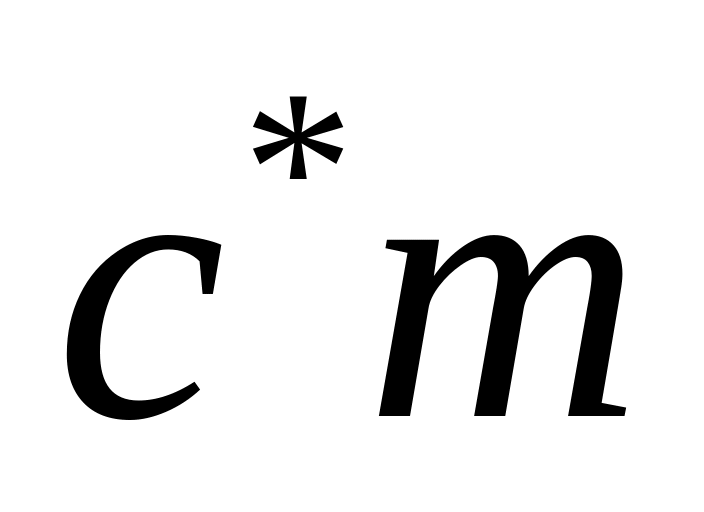 .
.Через полюс зацепления касательно к основным окружностям проводим линию зацепления. Точки касания
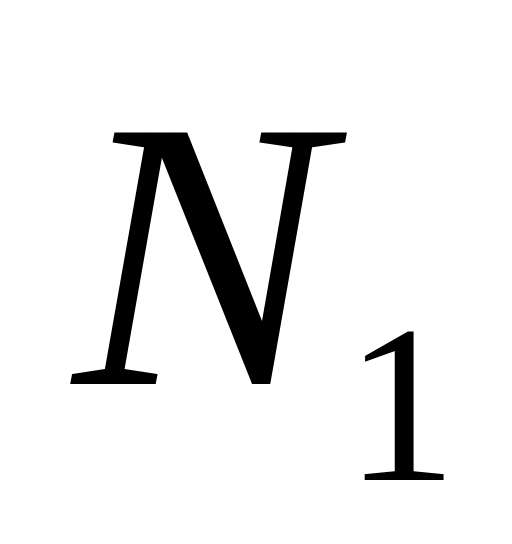 и
и
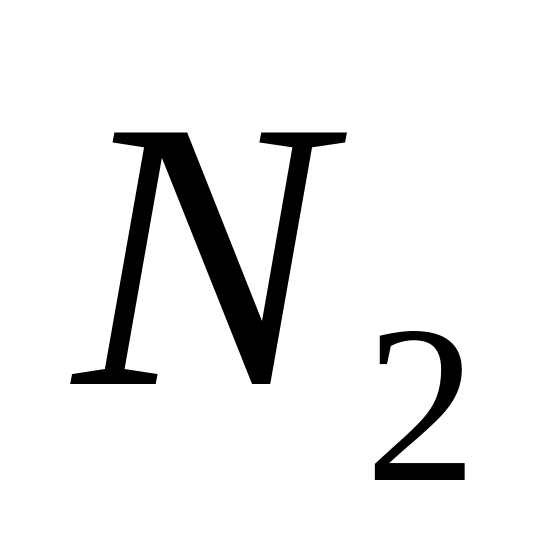 называются предельными точками линии
зацепления, которая образует с
перпендикуляром, восстановленным к
осевой линии в полюсе, угол зацепления.
Точками
называются предельными точками линии
зацепления, которая образует с
перпендикуляром, восстановленным к
осевой линии в полюсе, угол зацепления.
Точками
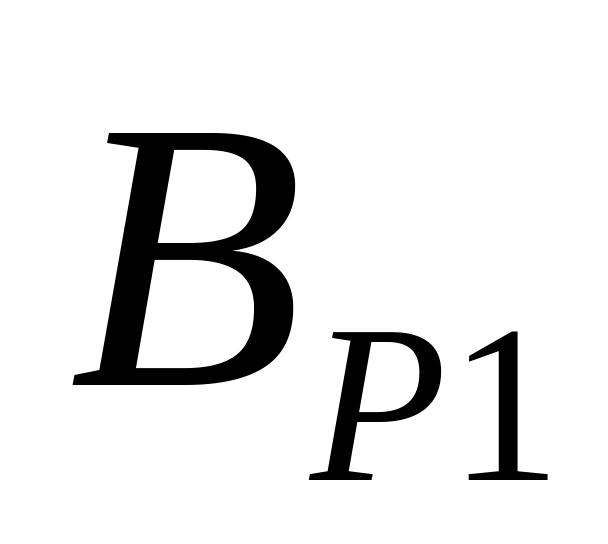 и
и
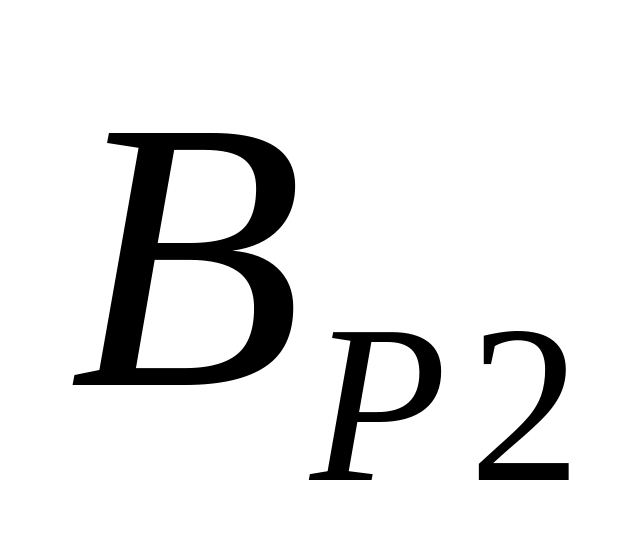 отмечена активная линия зацепления.
Точка
является точкой пересечения окружности
вершин колеса с линией зацепления, а
точка
является точкой пересечения окружности
вершин шестерни с линией зацепления.
Они называются соответственно точками
начала и конца зацепления.
отмечена активная линия зацепления.
Точка
является точкой пересечения окружности
вершин колеса с линией зацепления, а
точка
является точкой пересечения окружности
вершин шестерни с линией зацепления.
Они называются соответственно точками
начала и конца зацепления.На каждом колесе строят профили трех зубьев, причем точка контакта К должна располагаться на активной линии зацепления. Профиль шестерни получается соответствующим поворотом зубьев полученных в станочном зацеплении. Эвольвентная часть профиля колеса строится, как траектория точки прямой при перекатывании ее по основной окружности колеса без скольжения, и переносится в точку контакта зубьев К на линию зацепления. Переходная часть профиля зуба строится приближенно.
На чертеже указываются диаметры начальных, делительных, основных окружностей, окружности вершин и впадин, шаг и толщина зубьев по делительным окружностям, высота зуба, межосевое расстояние, воспринимаемое смещение, угол зацепления, радиальный зазор, положения профилей в точках начала и конца зацепления, углы торцевого перекрытия (
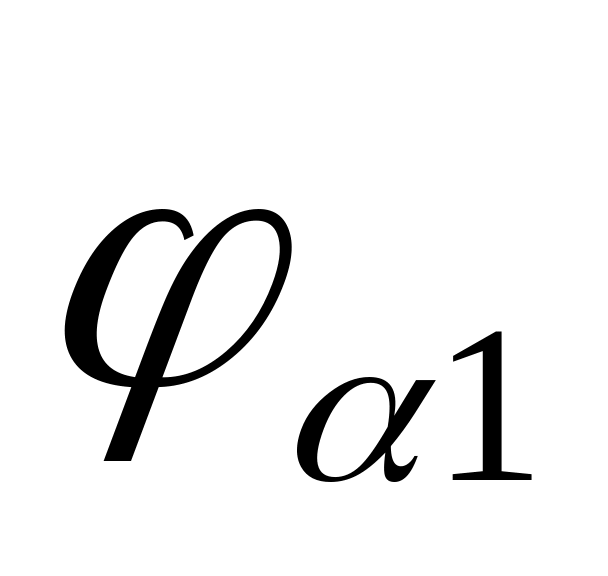 и
и
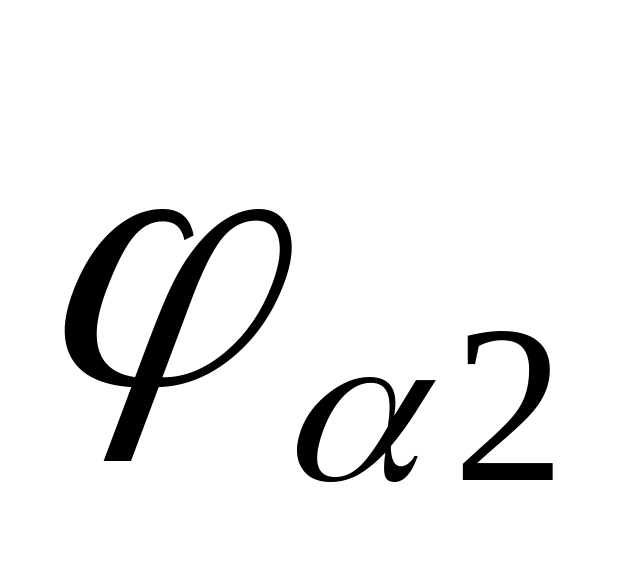 ).
).
3.3. Проектирование планетарного зубчатого механизма с цилиндричискими колесами.
При кинематическом синтезе многосателлитной планетарной передачи заданной схемы решаются задачи подбора таких чисел зубьев ее колес, которые будут удовлетворять условиям:
Выполнение заданного передаточного отношения;
Отсутствия заклинивания передачи, среза и подреза профилей зубьев колес;
Соосность входного и выходного валов;
Соседства;
Сборки.
Первые три условия являются общими требованиями синтеза любой планетарной передачи. Остальные – это условия, диктуемые особенностями кинематических схем планетарных механизмов. Для двухрядного планетарного механизма с одним внешним и одним внутренним зацеплением воспользуемся методом сомножителей для подбора чисел зубьев колес.
Планетарная коробка передач состоит из двухрядного планетарного редуктора смешанного зацепления с тремя сателитами. При проектировании редуктора используются следующие данные:
Передаточное отношение, U - 31/3;
Число сателитов, k - 3.
Проектируемый редуктор должен удовлетворять следующим требованиям:
1) Он должен обеспечивать необходимое передаточное отношение. Для этого записывают вырыжение, связывающее между собой количество зубьев колес планетарного редуктора (Z1,Z2,Z3,Z4) и заданное передаточное отношение. В нашем случае выражение имеет вид:
![]() .
.
2) Должно соблюдаться условие соосности, т.е. оси центральных колес при назначенных Z должны совпадать с осью водила. В нашем случае выражение условия соосности имеет вид:
Z1+Z2+Z3=Z4.
3) Должно выполняться условие соседства (совместности), т.е. должна быть возможность размещения нескольких сателитов по общей окружности в одной плоскости без соприкосновения друг с другом. Выражение условия соосности имеет вид:
![]() .
.
4) Должно соблюдаться условие сборки, т.е. должна обеспечиваться возможность одновременного зацепления всех сателлитов с центральными колесами при равных углах между сателитами:
![]() =n,
где n - целое число.
=n,
где n - целое число.
5)
Должно соблюдаться условие отсутствия
подрезания, т.е. при колесах нарезанных
стандартным инструментом без смещения
(при
![]() ;
;
![]() )
Zmin должно
быть больше 17, а Z4min
должно быть не меньше 85.
)
Zmin должно
быть больше 17, а Z4min
должно быть не меньше 85.
Исходя из условия наименьших габаритов находим:
Z1=18;
Z2=56;
Z3=37;
Z4=111
