1.3.2 Построение планов скоростей

Определение линейных скоростей точек механизма начинаем с входного звена АОС. Определим модуль окружной скорости точки А кривошипа. Точки А и С относительно точки 0 совершают вращатель­ное движение, поэтому векторы скоростей точек А и С направлены перпен­дикулярно кривошипу 1 в сторону его вращения, а модуль скоростей определяется из выражения:

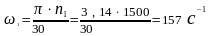
тогда

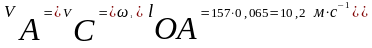
Далее определяем скорости точек структурных групп. Для этого составляем систему векторных уравнений, связывающих искомую скорость точки с известными скоростями точек. Для двухповодковых групп искомой всегда будет являться скорость средней кинемати­ческой пары, а известными - скорости точек концевых кинематичес­ких пар.

Построение плана скоростей начинаем с группы Ассура 2-3.

Составляем векторные уравнения для средней точки группы Ассура:

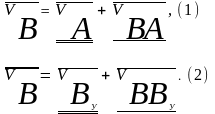
Условимся векторы, известные по модулю и направлению, под­чёркивать двумя чертами, а известные по направлению – одной чертой.

В этой системе векторных уравнений известны по модулю и нап­равлению векторы скоростей точек А и В_у (подчёркиваем двумя чертами):

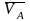– вектор скорости точки А, величина была определена выше, направлен перпендикулярно кривошипу 1, по направлению его вращения.

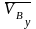– вектор скорости точки В_У по величине равен нулю.

Векторы отно­сительных скоростей известны только по направлению (подчёркиваем одной чертой):

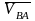– вектор относительной скорости звена АВ, во вращении его относительно точки (полюса) А, нап­равлен перпендикулярно звену АВ,

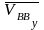– вектор относительной скорости ползуна 3, в движении его по направляющим у – у, направлен параллельно направляющим у – у.

В уравнениях четыре неизвестных параметра, определим их графическим решением векторных уравнений, т.е. путём построения планов скоростей.

Изображая скорость точки А отрезком Р_О а = 51мм, опреде­лим значение масштабного коэффициента:

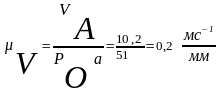
Последовательность графоаналитического решения задачи рассмотрим на примере построения плана скоростей для четвёртого положения точки А механизма, когда угол φ₁ = 120º. Для четвёртого положения механизма проводим из полюса Р_о вектор Р_оа₄ = 51мм перпендикулярно кривошипу ОА₄ в сторону его вращения. В соответствии с первым векторным урав­нением через точку а₄ проводим прямую, перпендикулярную звену АВ механизма (это линия вектора V_ВА), а в соответствия со вто­рым векторным уравнением из полюса Р_о проводим прямую, парал­лельную направляющим у – у. Точка пересечения этих двух прямых определяет точку в₄, которая является концом вектора Р₀в₄ изображающего на плане вектор скорости v_B4. Для определения действительной величины любого из полученных векторов достаточно умножить соответствующий отрезок в миллиметрах на масштабный коэффициент плана скоростей.

Из плана скоростей имеем:

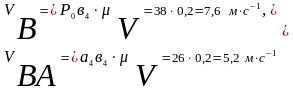
Скорость точки 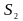– центра тяжести звена 2 найдем по теореме подобия:

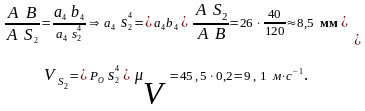
Теперь рассмотрим вторую группу Ассура 4-5.

Система векторных уравнений для данной группы будет иметь вид:

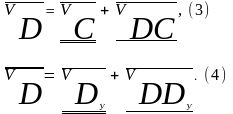
В этой системе векторных уравнений известны по модулю и нап­равлению скорости точек С и D_у (подчёркиваем двумя чертами).

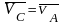– вектор скорости точки А, величина была определена выше, вектор скорости точки С направлен перпендикулярно кривошипу 1, по направлению его вращения.

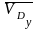– вектор скорости точки D_У, по величине равен нулю.

Векторы отно­сительных скоростей известны только по направлению:

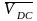– вектор относительной скорости звена CD, во вращении его относительно точки (полюса) C, нап­равлен перпендикулярно звену CD,

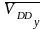– вектор относительной скорости ползуна 5, в движении его по направляющим у – у, направлен параллельно направляющим у – у.

Теперь строим планы скоростей для группы Ассура 4 – 5.

Скорости точки С смещены относительно скоростей точки А на 180°, так как точки А и С принадлежат одному звену и диаметраль­но противоположны. Планы скоростей строятся аналогично планам скоростей для группы Ассура 2 – 3.

В соответствии с планом скоростей для группы Ассура 4 – 5 имеем:

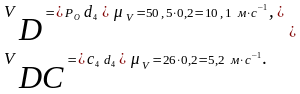
Для нахождения скорости точки S₄ - центра тяжести звена 4 воспользуемся теоремой подобия:

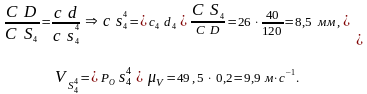
Скорости всех точек звеньев механизма и их отрезки в миллиметрах представлены в таблице 3.

Таблица 3 – Абсолютные и относительные скорости точек звеньев

механизма и их отрезки в миллиметрах

Обозначение	Единица	Положение механизма
		0 и 6	1 и 11	2 и 10	3 и 9	4 и 8	5 и 7
PО а	мм	51	51	51	51	51	51
VA	мּс-1	10,2	10,2	10,2	10,2	10,2	10,2
PО в	мм	0	31,5	50,5	51	38	19,5
VВ	мּс-1	0	6,3	10,1	10,2	7,6	3,9
a в	мм	51	44,5	26	0	26	44,5
VBA	мּс-1	10,2	8,9	5,2	0	5,2	8,9
РO s2	мм	34	40	49,5	51	45,5	37,5
VS2	мּс-1	6,8	8	9,9	10,2	9,1	7,5
PО с	мм	51	51	51	51	51	51
VC	мּс-1	10,2	10,2	10,2	10,2	10,2	10,2
РО d	мм	0	19,5	38	51	50,5	31,5
VD	мּс-1	0	3,9	7,6	10,2	10,1	6,3
с d	мм	51	44,5	26	0	26	44,5
VDC	мּс-1	10,2	8,9	5,2	0	5,2	8,9
PO s4	мм	34	37,5	45,5	51	49,5	40
VS4	мּс-1	6,84	7,5	9,1	10,2	9,9	8