2. Синтез эвольвентной зубчатой передачи.
2.1.Выполним геометрический расчёт цилиндрической прямозубой передачи, составленной из колёс 1 и 2 при свободном выборе межосевого расстояния.
Наименьшее число зубьев, которое можно нарезать без корригирования и без подреза:
.
Малое колесо имеет число зубьев z1=13, поэтому при его нарезании необходимо корригирование.
Необходимый коэффициент смещения:
.
Колесо 2 имеет число зубьев
,
поэтому его можно изготовить некорригированным. Принимаем
.
По основному уравнению зацепления определяем инволюту угла зацепления передачи
,
откуда сам угол зацепления будет равен
,
Определяем коэффициент воспринимаемого смещения:
Коэффициент уравнительного смещения:
.
Определяем геометрические размеры зубчатой передачи.
Диаметры делительных окружностей колёс:
,
.
Диаметры основных окружностей:
,
.
Радиусы начальных окружностей:
,
.
Межосевое расстояние:
.
Проверка этого результата даёт
.
Вычисления верны
Диаметры окружностей вершин зубьев:
Диаметры окружностей впадин:
Высота зуба:
.
Толщины зубьев по делительным окружностям колёс:
,
.
Проверка произведённого расчёта:
,
.
Угол давления на окружности вершин меньшего колеса:
.
Угол давления на окружности вершин большего колеса:
.
Проверка зуба малого колеса на заострение:
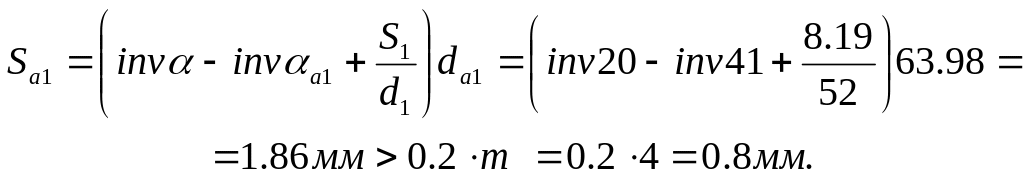
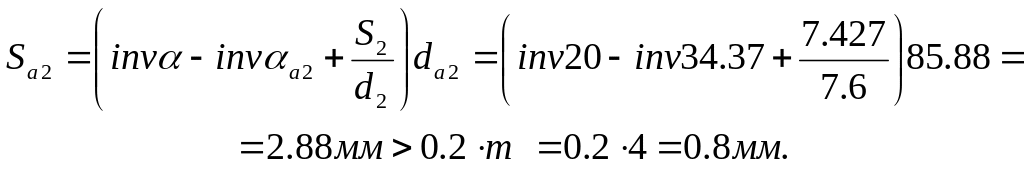
Шаг зацепления
Коэффициент перекрытия зубчатой передачи:
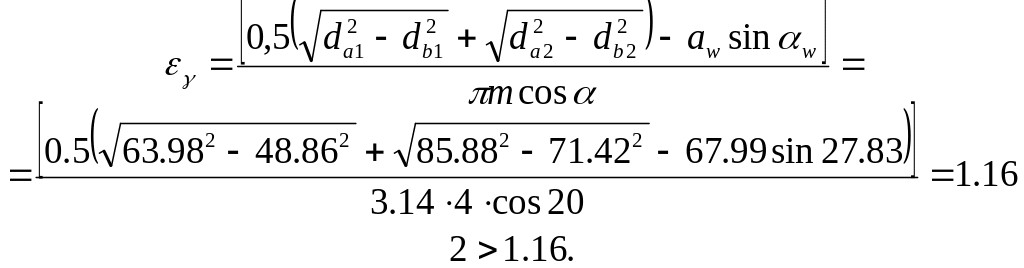
2.2.. Построение графика удельного скольжения.
График строим в системе λOxk, в которой ось ординат проводим как продолжение линии O1N1, а ось абсцисс — параллельно линии зацепления N1N2. Обозначим абсциссу произвольной точки K на линии зацепления через xk. Тогда удельные скольжения будут равны
,
.
Здесь
.
Определив
значения λ1
и λ2,
строим их графики (см. Лист 1 и рис. 3). При
,
;
при
,
.
-
Рис. 3. График удельного скольжения
2.3.. Построение графика удельного давления.
График строим в системе λOxk, в которой ось ординат проводим как продолжение линии O1N1, а ось абсцисс — параллельно линии зацепления N1N2. Обозначим абсциссу произвольной точки K на линии зацепления через xk. Тогда удельные скольжения будут равны
.
Определив
значения υ,
строим его график (см. Лист 1 и рис. 4). При
и
.
|
Рис. 4. График удельного давления |
3. Синтез планетарного редуктора.
3.1. Требуемое передаточное число планетарного механизма (см. п. 1):
.
По формуле Виллиса:
,
.
Условие обеспечения требуемого передаточного отношения:
,
. 
(4.1)
3.2. Условие соосности:
, (4.2)
3.3. Условие соседства:
Условие соседства для первой ступени планетарного редуктора:
,
.
(4.3)
3.4. Условие сборки:
. (4.4)
3.5. Условия отсутствия подреза:
(4.5)
3.6. Условия (4.1)-(4.5) выполняются, например, для z1=54, z2=57, z3=168,. Проверим это. Передаточное отношение:
.
Условие сборки выполняется при N=1, Ц=296
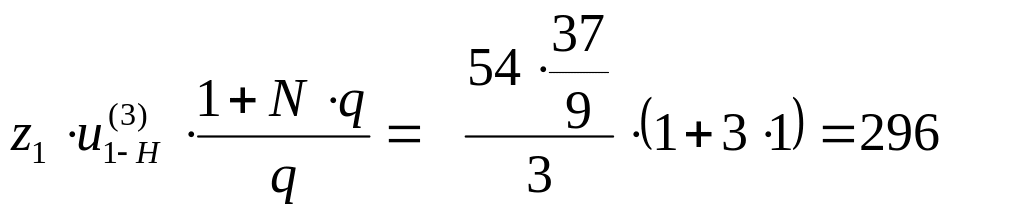
Условия соседства:
-
верно
Определяем диаметры начальных окружностей колёс.
,
,
,
Вычерчиваем схему редуктора (см. Лист 1), приняв диаметры начальных окружностей колёс 1 и 2
,
.
на основании геометрического расчёта. Масштабом построения зададимся из условия размещения схемы на листе
.
Угловая скорость зубчатого колеса z1:
.
Скорость точки А:
.
Строим картину линейных (см. рис. 5 и Лист 1) и угловых (см. рис. 6 и Лист 1) скоростей.
-
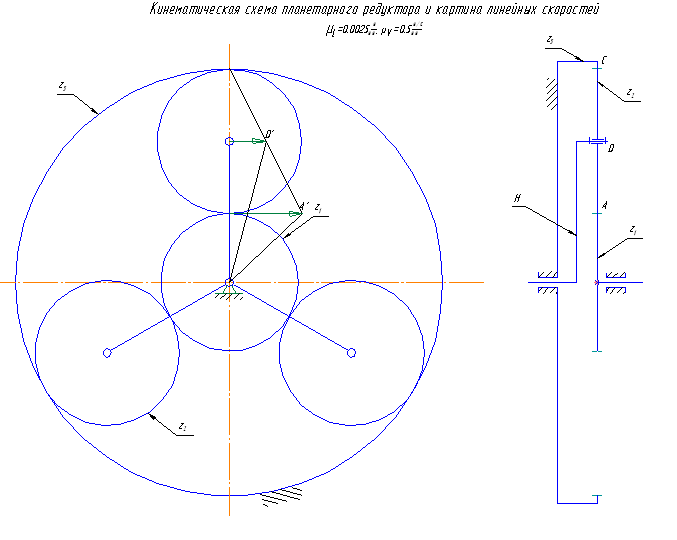
Рис. 5. Кинематическая схема планетарного редуктора и картина линейных скоростей
-
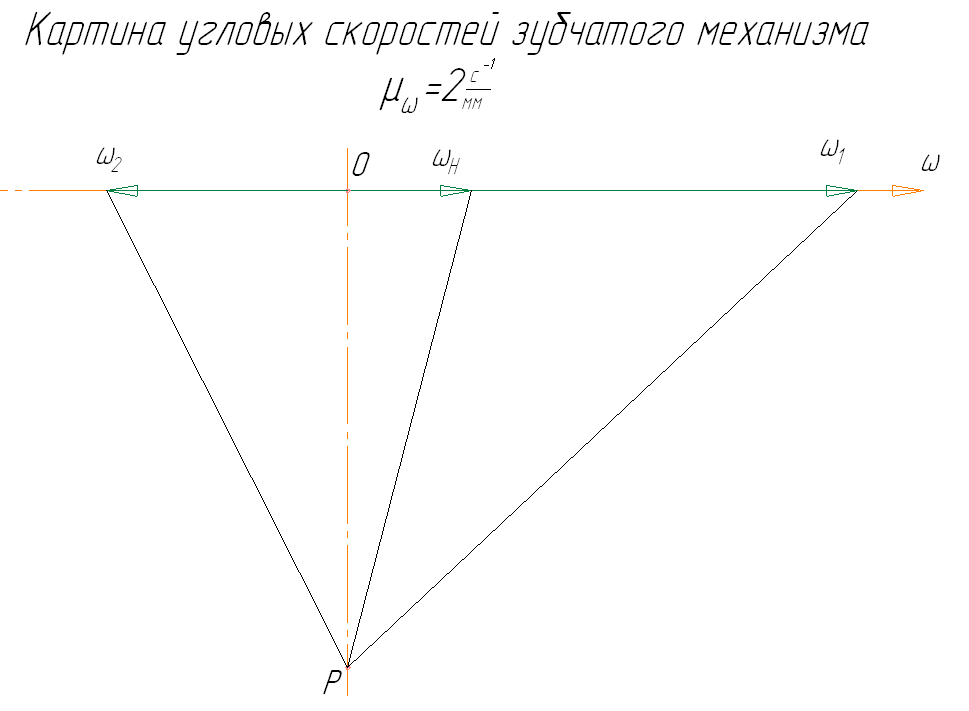
Рис. 6. Картина угловых скоростей планетарного редуктора