Выбор электродвигателя

Потребляемая мощность привода (мощность на выходе):

,

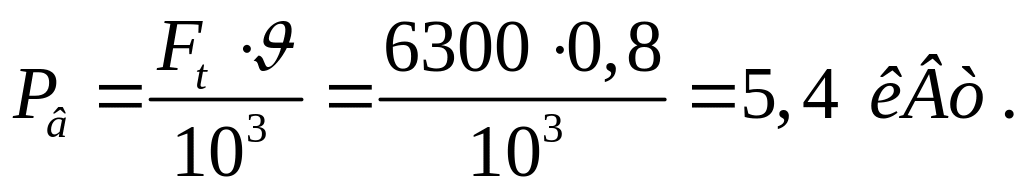
где η_муф = 0,98, η_подш = 0,99, η_зуб = 0,98, тогда:

.

Таким образом, требуемая мощность электродвигателя, равная

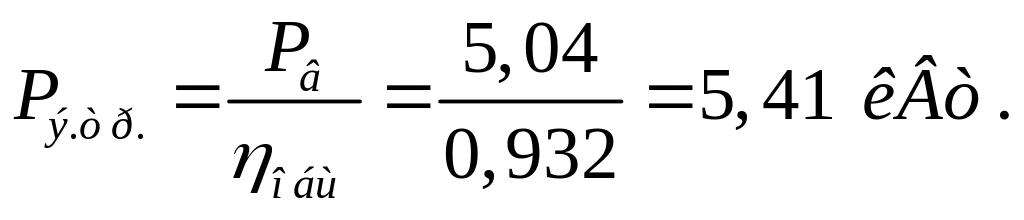
Делительный диаметр звёздочки:

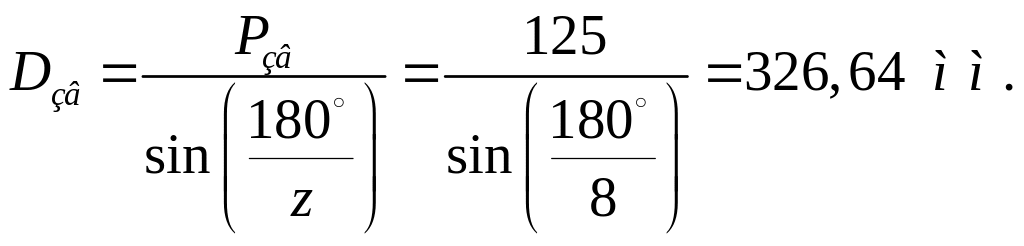
Частота вращения выходного вала редуктора:

,

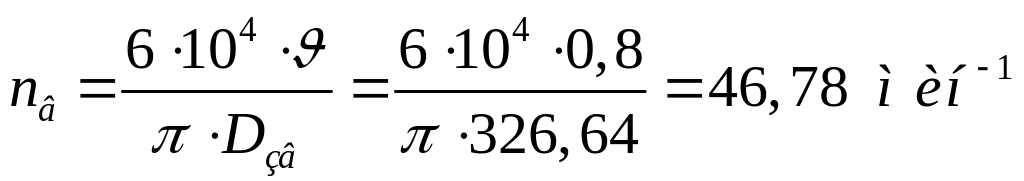По таблице с данными двигателей серии АИР, выбран двигатель мощностью 5,5 кВт АИР 132S6/960 (d_вала = 38мм).

Вращающий момент на тихоходном валу:

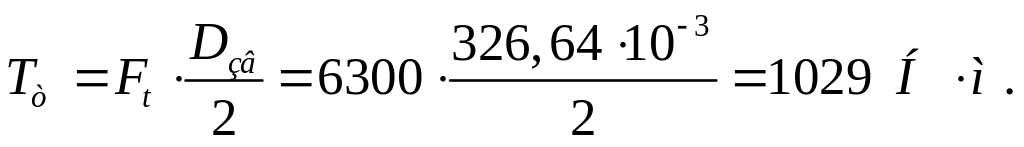
Предварительный расчет валов

Крутящий момент в поперечных сечениях валов

Быстроходного T_б = 51 Hм

Промежуточного T_пр = 202 Hм

Тихоходного T_т = 1029 Hм

Предварительные значения диаметров(мм) различных участков стальных валов редуктора:

1. для тихоходного вала:

Из ряда нормальных линейных размеров по ГОСТ 6636-69 принято значение d = 51 мм.

Из ряда нормальных линейных размеров по ГОСТ 6636-69 принято значение d_бп = 71 мм.

Тогда принимаем согласно тому же госту d_к = 71 мм.

2. для промежуточного вала:

Из ряда нормальных линейных размеров по ГОСТ 6636-69 принято значение d_к = 40 мм.

Из ряда нормальных линейных размеров по ГОСТ 6636-69 принято значение d_бк = 45 мм.

Так как это посадочный диаметр под подшипник, то принято значение диаметра d_п = 35 мм.

Из ряда нормальных линейных размеров по ГОСТ 6636-69 принято значение d_бп = 40 мм.

3) Быстроходная шестерня является насадной и поэтому ее внутренний диаметр равен диаметру концевого участка вала. D = 38 мм.

Расстояния между деталями редуктора

Чтобы поверхности корпуса вращающихся колес не задевали за внутренние поверхности стенок корпуса, между ними оставляют зазор «а», мм:

где L – расстояние между внешними поверхностями деталей передач, мм.

Для рассчитываемого редуктора:

Вычисленное значение а округляем в большую сторону:

Расстояние b₀ между дном корпуса и поверхностью колеса быстроходной ступени принято равным 22мм.

Конструирование цилиндрических зубчатых колес внешнего зацепления.

Так как производство зубчатых колес мелкосерийное то, экономически целесообразна ковка колес в простейших односторонних прокладных штампах.

Определение длины ступиц зубчатых колёс:

Определение ширины S торца зубчатого венца:

Величина фаски на торце зубчатого венца:

приннято

Т.к. твердость рабочих поверхностей выше 350 НВ, то фаски выполняют под углом 45°.

Величины фасок на торцах ступиц (1,6мм для колеса быстроходной ступени и 2мм для колеса тихоходной) выбраны в зависимости от диаметров валов.

Толщина диска:

, где

где:

Для свободной выемки заготовок из штампа взяты значения штамповочных уклонов γ ≥ 7° и радиусов закруглений R ≥ 6мм.

Расчет шпоночного соединения.

1) Для концевого участка тихоходного вала редуктора и концевого участка приводного вала:

– диаметр вала,

– момент на валу.

k = 0,47h – выступающая часть шпонки.

Расчет ведётся по формуле:

[2, с.92]

Допускаемое напряжение на смятие

Принято [1, с.476, табл.24.29]

2) Для тихоходного вала редуктора:

– диаметр вала,

– момент на валу.

k = 0,47h – выступающая часть шпонки.

Допускаемое напряжение на смятие

Принято [1, с.476, табл.24.29]

3) Для промежуточного вала редуктора:

– диаметр вала,

– момент на валу.

k = 0,47h – выступающая часть шпонки.

Допускаемое напряжение на смятие

Принято [1, с.476, табл.24.29]

Проверка на срез:

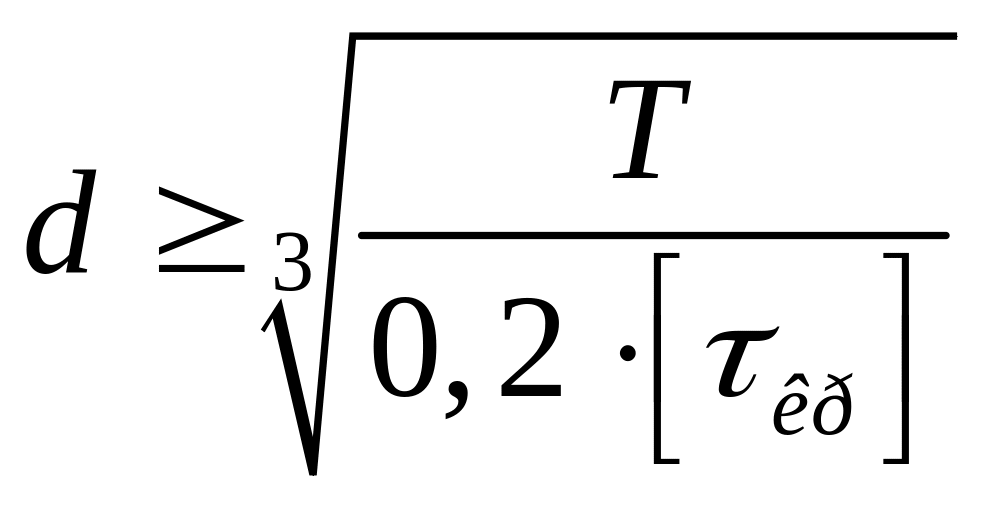, [τ_кр] = 40 Мпа.

1) 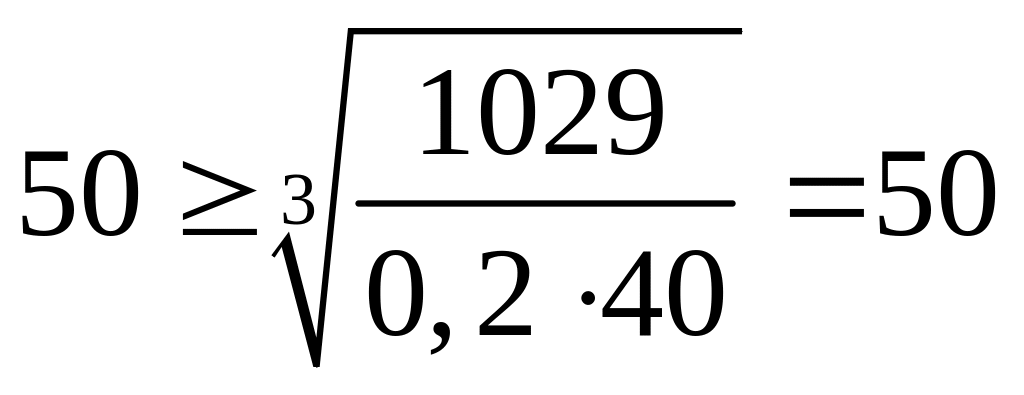– верно.

2) 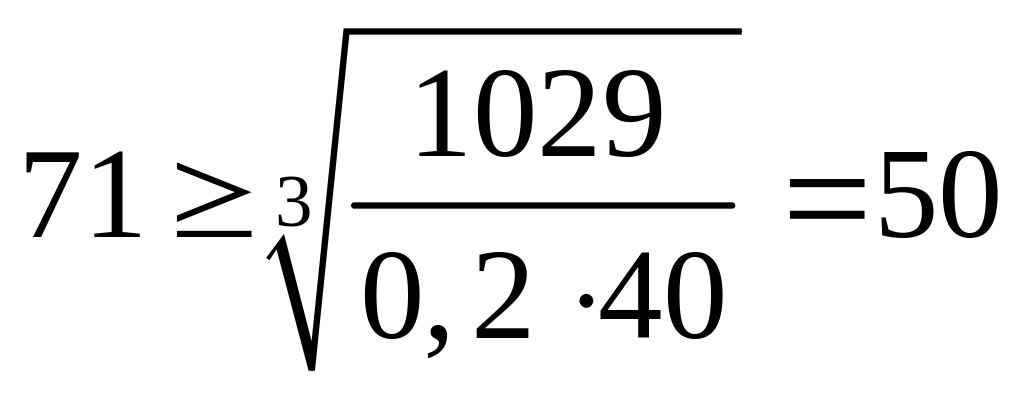– верно.

3) 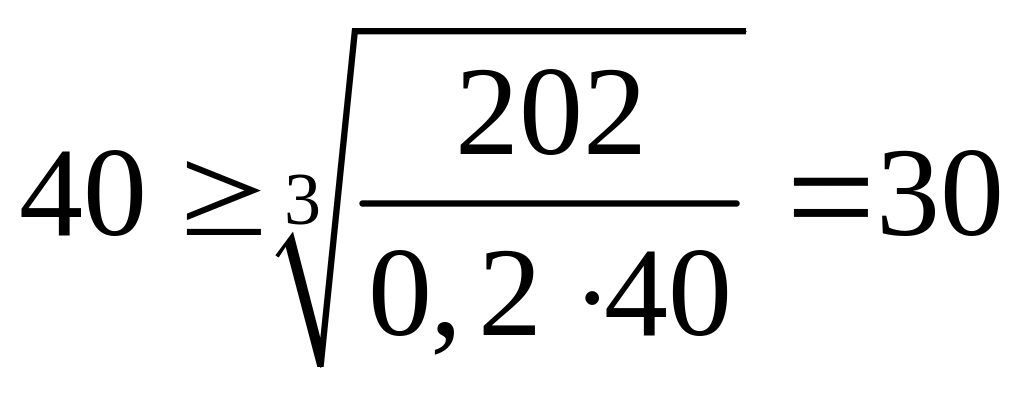– верно.

Подбор подшипников качения на заданный ресурс.

Расчет подшипников промежуточного вала.

1. Радиальные реакции опор от сил в зацеплении определяем из уравнения равновесия:

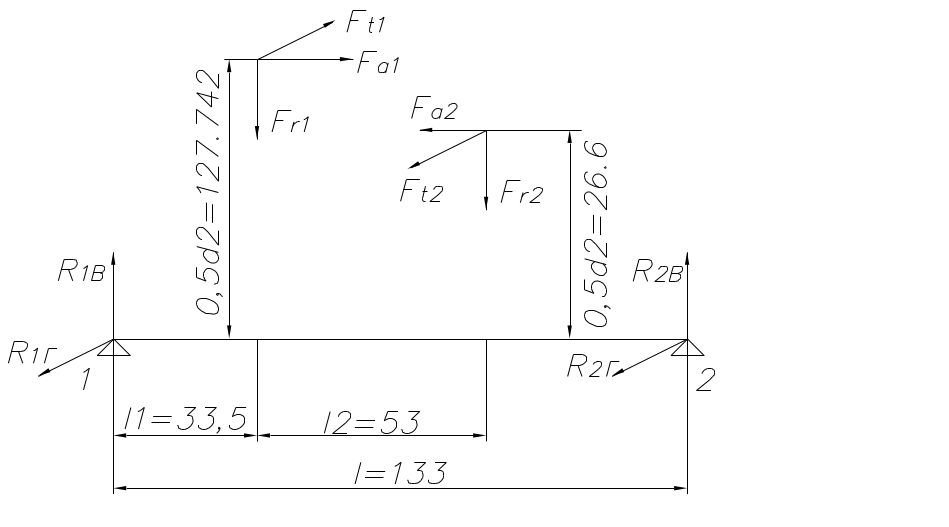
В плоскости YOZ:

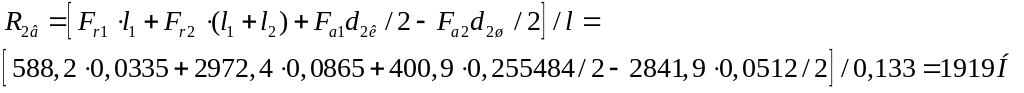
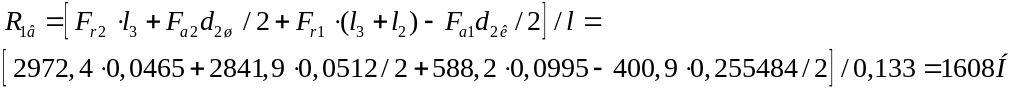
В плоскости XOY:

Суммарные реакции опор:

Н

Расчёт ресурса подшипников 207 ГОСТ 8338-75(С_r = 25,5кН, С_0r = 13,7кН):

Для типового режима нагружения III коэффициент эквивалентности К_Е = 0,56.

Вычисление эквивалентных нагрузок:

Для опоры 1:

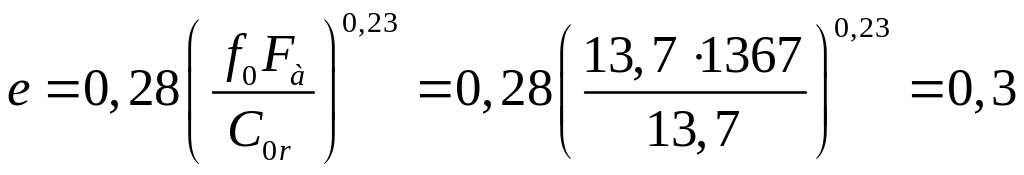
Экивалентная динамическая радиальная нагрузка для подшипника опоры 1 при К_б = 1,4 и К_Т = 1 (t < 100°).

Скорректированный ресурс для подшипника опоры 1:

а₁ = 1(вероятность безотказной работы 90%);

а₂₃ = 0,75;

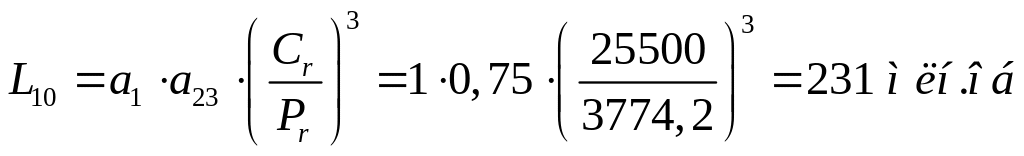
Проверка выполнения условия

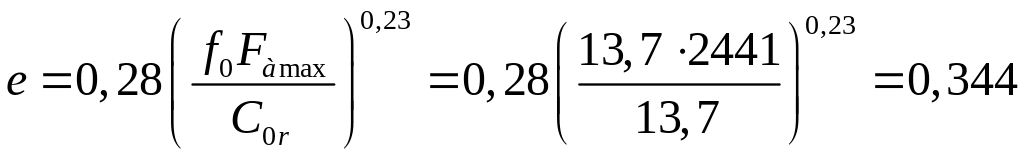
– верно.

Экивалентная динамическая радиальная нагрузка для подшипника опоры 2 при К_б = 1,4 и К_Т = 1 (t < 100°).

e = 0, X = 1, Y = 0.

Скорректированный ресурс для подшипника опоры 1:

а₁ = 1 (вероятность безотказной работы 90%);

а₂₃ = 0,75;

e = 0, X = 1, Y = 0.

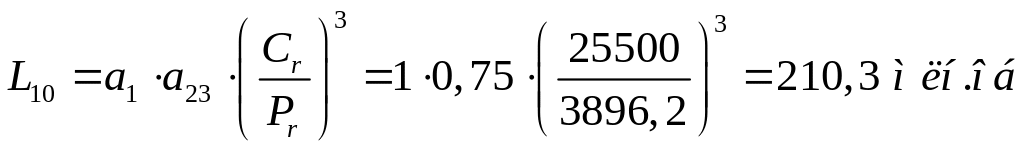
Проверка выполнения условия

– верно.

Пара подшипников 207 ГОСТ 8338-75 удовлетворяет расчетному ресурсу 10000 часов.

Расчет подшипников тихоходного вала.

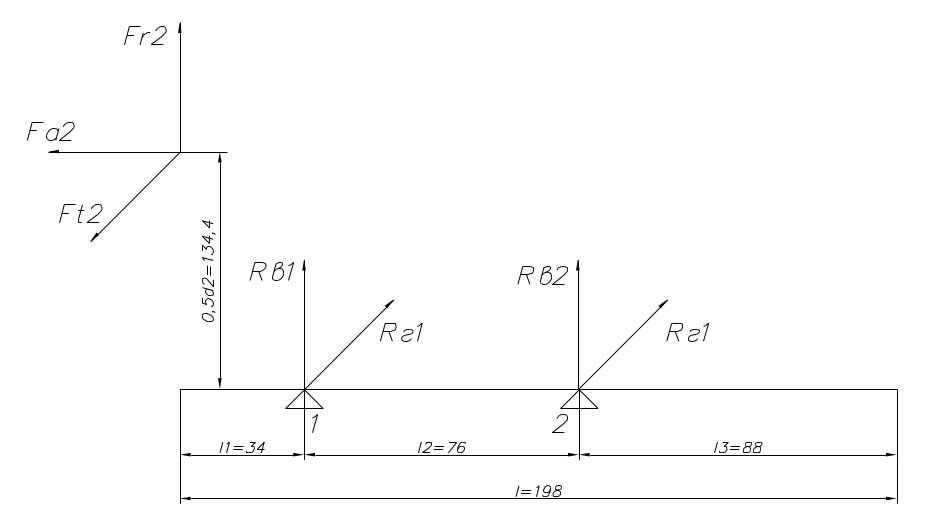
В плоскости YOZ:

;

;

В плоскости XOY:

Определение консольной силы:

где С_р – радиальная жёсткость упругой муфты при радиальном смещении валов, Н/мм. Для муфты со стальными стержнями в осевом направлении С_р вычисляют по формуле T_н номинальный крутящий момент. Δ = 0,7мм, так как расстояние между осью вала и опорной плоскостью больше 250 мм.

Таким образом, .

; ;

; .

Суммарные реакции опор:

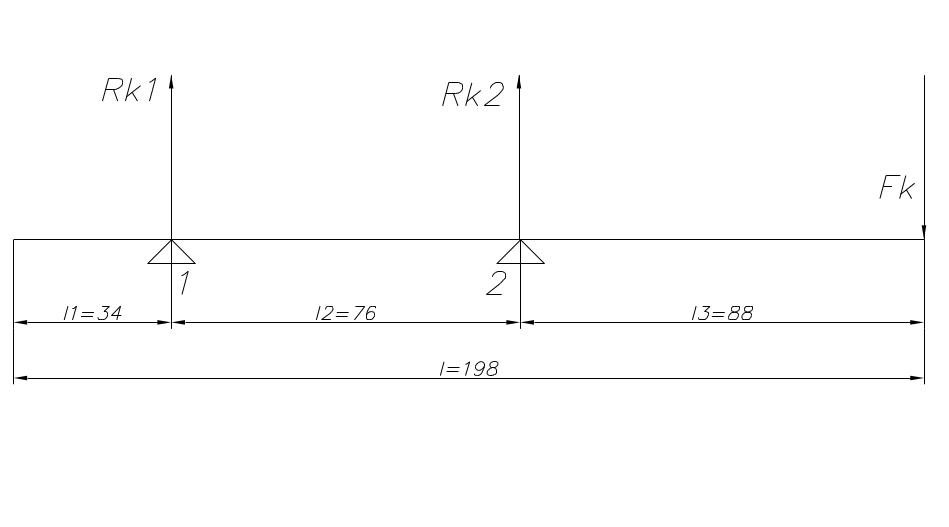F_r1max = 12578Н, F_r2max = 7784Н, F_Аmax = 2841,9Н.

Для типового режима нагружения III коэффициент эквивалентности К_Е = 0,56. Аналогично расчёту промежуточного вала К_б = 1,4 и К_Т = 1 (t < 100°).

Вычисление эквивалентных нагрузок:

Расчёт ресурса подшипников 7212А ГОСТ 27365-87 (С_r = 91,3кН, е = 0,4, С_0r=70,0кН):

Минимально необходимые для нормальной работы радиально-упорных подшипников осевые силы

то F_a1 = F_a1min =2338,6H;

F_a2 = F_a1 + F_A =2338,6 + 1591 = 3929,6H.

.

.

Экивалентная динамическая радиальная нагрузка для подшипников,

X = 1, Y = 0.

Определение расчётного скорректированного ресурса наиболее нагруженного подшипника опоры 2:

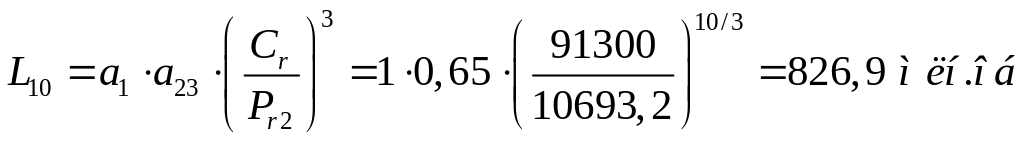
Проверка выполнения условия

– верно.

Пара подшипников 7212А ГОСТ 27365-87 удовлетворяет расчетному ресурсу 10000 часов.

Расчёт на прочность промежуточного вала.

1. Определение внутренних силовых факторов.

Реакции опор от сил, нагружающих вал, определены при расчете подшипников вала. Эпюры внутренних силовых факторов приведены на рисунке.

Из рассмотрения эпюр внутренних силовых факторов и конструкции узла следует, что опасными являются сечения:

I – I – место установки зубчатого колеса на вал диаметром 40 мм: сечение нагружено изгибающими и крутящим моментами, осевой силой; концентратор напряжений – шпоночный паз;

II – II – центр тихоходной шестерни.

Определим силовые факторы для опасных сечений.

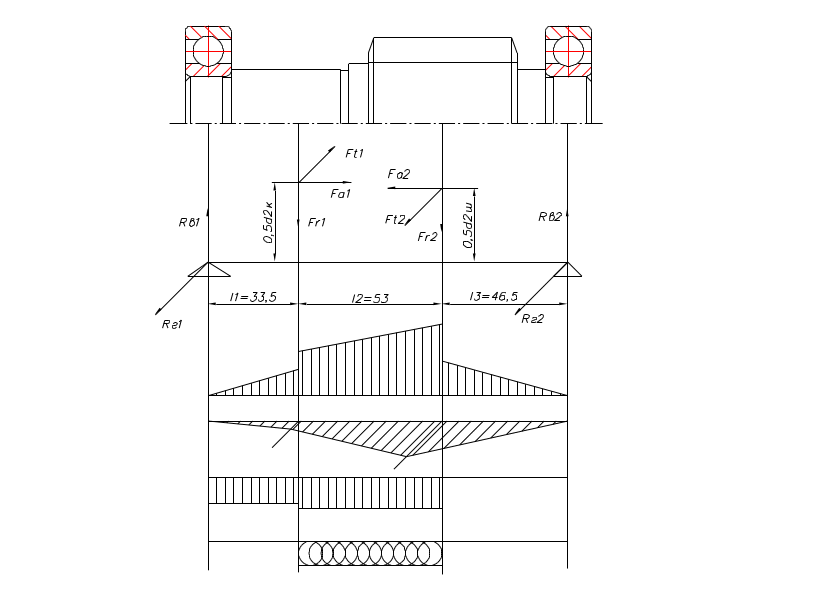
Сечение I – I

Изгибающие моменты:

- в плоскости XOZ

- в плоскости YOZ слева от сечения

- в плоскости YOZ справа от сечения

- момент от консольной силы

Суммарный изгибающий момент

Крутящий момент

Осевая сила

Сечение II – II

Изгибающий момент

Крутящий момент

Осевая сила