- •2.2.2 Определение величины межосевого расстояния из расчета прочности по контактным напряжениям
- •1.Энерго-кинематический расчет привода и выбор двигателя
- •1.1 Исходные данные
- •1.2 Расчет кпд и выбор электродвигателя
- •1.3 Общее передаточное число привода и разбивка по отдельным ступеням передач
- •1.4 Частоты вращения и крутящие моменты на валах
- •2 Расчет передаточных механизмов
- •2.1 Проектировочный расчет зубчатой цилиндрической косозубой передачи внешнего зацепления
- •2.1.1 Определение допускаемых напряжений
- •2.1.2 Определение величины межосевого расстояния из расчета прочности по контактным напряжениям
- •2.1.3 Определение значения модуля из расчета прочности по напряжениям изгиба
- •2.1.4 Расчет коэффициента динамичности нагрузки
- •2.2.1 Определение допускаемых напряжений
- •2.2.2 Определение величины межосевого расстояния из расчета прочности по контактным напряжениям
- •2.2.3 Определение значения модуля из расчета прочности по напряжениям изгиба
- •2.2.4 Расчет коэффициента динамичности нагрузки
- •2.3.2 Определение геометрических размеров передачи
- •2.3.3 Проверка статистической прочности на разрыв
- •3 Расчет валов редуктора
- •3.1 Нагрузки, приложенные к валам
- •3.2 Предварительный расчет валов
- •3.3 Проверочный расчет валов
- •4 Подбор и расчет шпонок и подшипников
- •4.1 Подбор и расчет на смятие шпонок
- •4.2 Подбор и расчет подшипников
- •Список рекомендуемой литературы:
2.3.3 Проверка статистической прочности на разрыв
Предельная нагрузка, вызывающая разрыв цепи
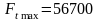 Н. (2.91)
Н. (2.91)
Поскольку выполняется неравенство
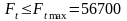 Н,
Н,
то условие статической прочности на разрыв выполнено.
3 Расчет валов редуктора
3.1 Нагрузки, приложенные к валам
Детали, размещенные на валах, как правило, находятся под воздействием сосредоточенных или распределенных сил, а также изгибающих и крутящих моментов, которые деформируют вал и вызывают внутри него появление напряжений. Так как при статических расчетах приходится оперировать моделями, то размещенные на валу детали заменяются системой реактивных сил и моментов.
Опорами валов служат подшипники. Нагрузки в виде системы сосредоточенных и распределенных сил, а также изгибающих и крутящих моментов, должны быть приложены к геометрической оси вала. С этой целью силовые факторы переносятся из точек их фактического приложения в точки, лежащие на оси вала, известными методами механики. Реакция подшипника на вал представляется в виде сосредоточенной силы, точка приложения которой лежит в месте пересечения нормали в контакте тела качения с дорожкой в оси вала. Если реакция, действующая на вал со стороны подшипника, распределена вдоль шейки вала по некоторому закону, то точка приложения реакции является точкой приложения результирующей.
Обычно внешние нагрузки, приложенные к валу, не лежат в одной плоскости, вот почему их следует представлять в виде проекций на два взаимно перпендикулярных направления. Выполнив необходимые расчеты для каждой из двух взаимно перпендикулярных плоскостей, окончательный результат можно получить геометрическим сложением составляющих.
Внешние нагрузки вызывают в сечении вала нормальные и касательные напряжения. Нормальные напряжения возникают вследствие изгибающего момента, а касательные – как из-за наличия момента кручения, так и из-за поперечных сил. Последним видом напряжений, в силу их малости, обычно пренебрегают.
3.2 Предварительный расчет валов
Для
валов (рис. 4) используем сталь 40Х (ГОСТ
4543-80) с термическим улучшением: закалка
с высоким отпуском. Данный материал в
сочетании с термическим улучшением
обеспечивает следующие свойства:
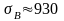 МПа;
МПа;
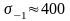 МПа;
МПа;
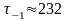 МПа;
МПа;
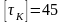 МПа.
МПа.
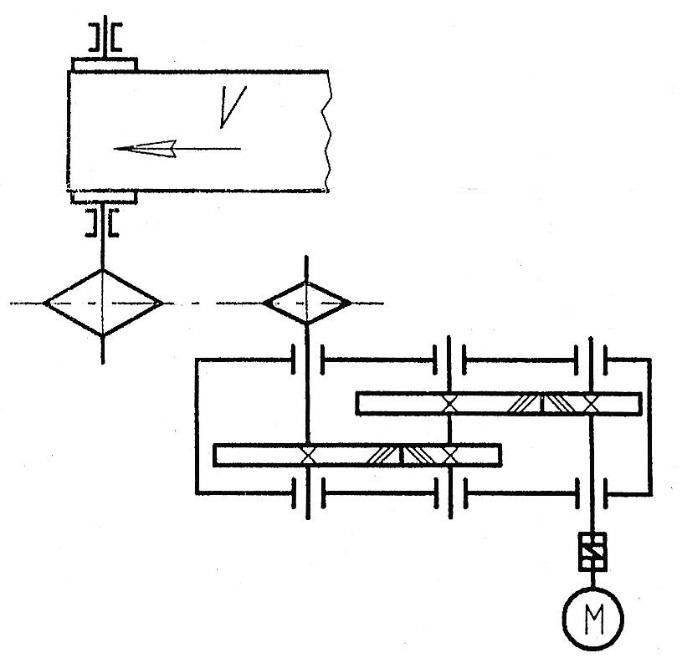
Рисунок 3.1 – Кинематическая схема привода
Предварительный расчет диаметров выходных концов валов осуществляем из расчета на кручение по формулам:
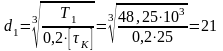 мм, по ГОСТ
6636-69 принимаем
32мм; (3.1)
мм, по ГОСТ
6636-69 принимаем
32мм; (3.1)
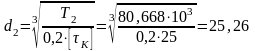 мм,
по ГОСТ 6636-69
принимаем 30мм:
мм,
по ГОСТ 6636-69
принимаем 30мм:
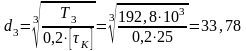 мм,
по ГОСТ 6636-69
принимаем
35мм;
мм,
по ГОСТ 6636-69
принимаем
35мм;
Диаметры остальных участков валов назначаем, исходя из конструктивных соображений при компоновке редуктора.
3.3 Проверочный расчет валов
Первый вал.
-
крутящий момент на валу
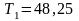 Н·м;
Н·м;
-
делительный диаметр шестерни
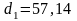 мм;
мм;
-окружная
сила
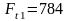 H;
H;
-
радиальная сила
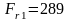 H;
H;
-
осевая сила
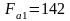 H.
H.
Строим эпюры изгибающих моментов в горизонтальной плоскости.
Определяем опорные реакции.
Силовые реакции опор определяем из условия уравновешенности моментов в горизонтальной и вертикальной плоскости относительно каждой из опор.
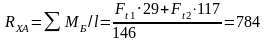 Н (3.2)
Н (3.2)
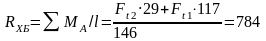 Н
Н
- проверяем правильность определенных реакций
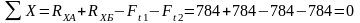 . (3.3)
. (3.3)
-
строим эпюры изгибающих моментов
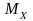 ,
для чего определяем их значение в
характерных сечениях вала:
,
для чего определяем их значение в
характерных сечениях вала:
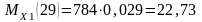 Н·м; (3.4)
Н·м; (3.4)
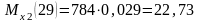 Н·м.
Н·м.
В вертикальной плоскости:
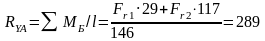 Н (3.5)
Н (3.5)
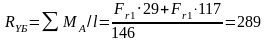 Н
Н
Проверяем правильность определенных реакций:
(3.6)
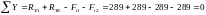
-
строим эпюры изгибающих моментов
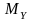 ,
для чего определяем их значение в
характерных сечениях вала:
,
для чего определяем их значение в
характерных сечениях вала:
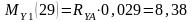 Н·м;
Н·м;
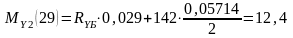 Н·м.
Н·м.
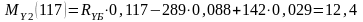 Н·м,
Н·м,
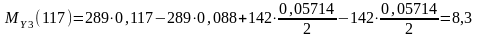 Н·м.
Н·м.
Строим
эпюру крутящих моментов. Крутящий
момент, передаваемый вдоль вала от
середины ступицы муфты до середины
первой шестерни равен
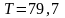 Н·м.
Н·м.
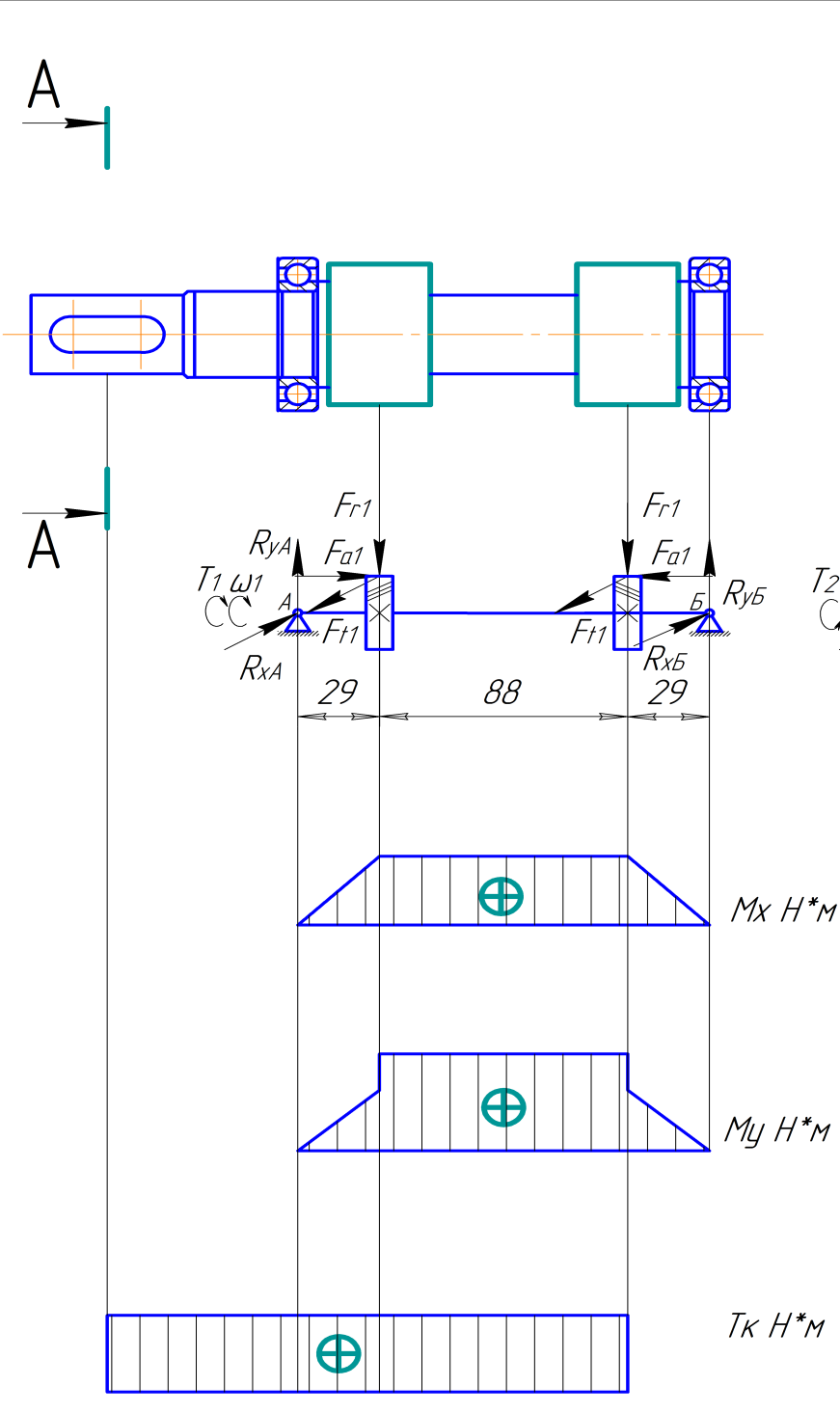
Рисунок 3.2 - Расчетная схема 1-го вала
Уточненный
расчет состоит в определении коэффициентов
запаса прочности
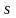 для опасных сечений и сравнении их с
требуемыми (допускаемыми) значениями.
для опасных сечений и сравнении их с
требуемыми (допускаемыми) значениями.
В
соответствии с формой вала и эпюрами
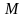 и
и
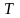 предположительно опасными сечениями
вала, подлежащими проверке на усталостную
прочность, являются сечения, в которых
имеются концентраторы напряжений и
возникают наибольшие моменты.
предположительно опасными сечениями
вала, подлежащими проверке на усталостную
прочность, являются сечения, в которых
имеются концентраторы напряжений и
возникают наибольшие моменты.
Определяем запас усталостной прочности в сильно нагруженном сечении А – А, в котором концентрация напряжений обусловлена шпоночной канавкой.
Коэффициент запаса прочности по напряжениям кручения определятся по формуле:
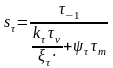 ,
(3.7)
,
(3.7)
где
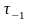 – предел выносливости при кручении;
– предел выносливости при кручении;
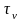 ,
,
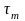 – соответственно амплитуда и среднее
значение напряжения отнулевого цикла;
– соответственно амплитуда и среднее
значение напряжения отнулевого цикла;
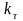 – коэффициент
концентрации напряжений кручения,
принимаем для шпоночного участка вала
– коэффициент
концентрации напряжений кручения,
принимаем для шпоночного участка вала
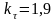 ;
;
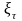 – масштабные
факторы, принимаем
– масштабные
факторы, принимаем
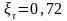 ;
;
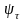 – коэффициент
влияния среднего напряжения цикла на
усталостную прочность, для легированных
сталей
– коэффициент
влияния среднего напряжения цикла на
усталостную прочность, для легированных
сталей
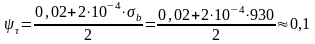 .
(3.8)
.
(3.8)
Осевой момент сопротивления:
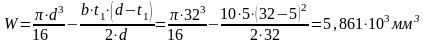 . (3.9)
. (3.9)
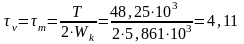 . (3.10)
. (3.10)
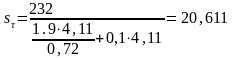 .
.
Коэффициент запаса прочности по нормальным напряжениям определяем аналогично:
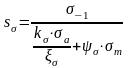 (3.11)
(3.11)
где
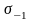 – предел выносливости при изгибе;
– предел выносливости при изгибе;
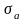 ,
,
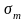 – соответственно амплитуда переменных
напряжений и среднее значение напряжения
цикла (Учитывая характер работы вала,
можно, если противное не обговорено
особо, закон изменения вызванных изгибом
нормальных напряжений считать
симметричным, а сжатием и растяжением
по отношению к изгибу пренебречь. При
таких допущениях
– соответственно амплитуда переменных
напряжений и среднее значение напряжения
цикла (Учитывая характер работы вала,
можно, если противное не обговорено
особо, закон изменения вызванных изгибом
нормальных напряжений считать
симметричным, а сжатием и растяжением
по отношению к изгибу пренебречь. При
таких допущениях
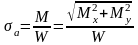 ,
,
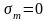 .
Учитывая силу и момент от муфты для
нашего сечения А-А,
.
Учитывая силу и момент от муфты для
нашего сечения А-А,
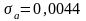
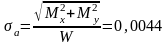 );
);
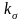 – коэффициент
концентрации напряжений изгиба, принимаем
для шпоночного участка вала
– коэффициент
концентрации напряжений изгиба, принимаем
для шпоночного участка вала
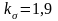 ;
;
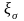 – масштабные
факторы, принимаем
– масштабные
факторы, принимаем
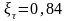 ;
;
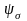 – коэффициент
асимметрии цикла, учитывающий влияние
средних напряжений на величину усталостной
прочности,
– коэффициент
асимметрии цикла, учитывающий влияние
средних напряжений на величину усталостной
прочности,
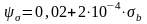 .
.
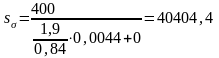
Расчетный коэффициент запаса прочности для сечения А-А:
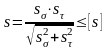 , (3.12)
, (3.12)
где
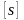 =1,5…2,5
=1,5…2,5
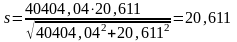 .
.
Такой большой коэффициент запаса прочности объясняется увеличением диаметра вала для соединения его стандартной муфтой с валом электродвигателя.
По той же причине проверять прочность в других сечениях нет необходимости.
Второй вал.
-
крутящий момент на валу
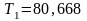 Н·м;
Н·м;
-окружная
сила:
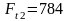 H;
H;
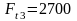 H;
H;
-
радиальная сила:
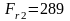 H;
H;
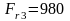 H;
H;
-
осевая сила:
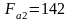 H;
H;
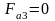 H.
H.
Строим эпюры изгибающих моментов в горизонтальной плоскости.
Определяем опорные реакции.
Силовые реакции опор определяем из условия уравновешенности моментов в горизонтальной и вертикальной плоскости относительно каждой из опор.
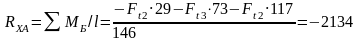 Н
Н
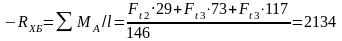 Н
Н
- проверяем правильность определенных реакций:
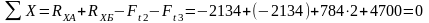
- строим эпюры изгибающих моментов , для чего определяем их значение в характерных сечениях вала:
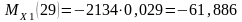 Н·м;
Н·м;
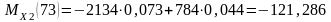 Н·м.
Н·м.
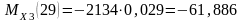 Н·м;
Н·м;
В вертикальной плоскости:
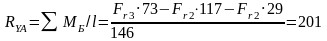 Н
Н
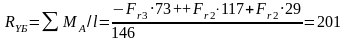 Н
Н
Проверяем правильность определенных реакций:
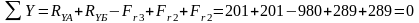
-
строим эпюры изгибающих моментов
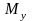 ,
для чего определяем их значение в
характерных сечениях вала:
,
для чего определяем их значение в
характерных сечениях вала:
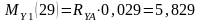 Н·м;
Н·м;
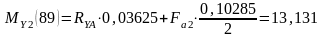 Н·м;
Н·м;
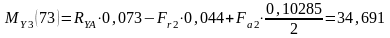 Н·м;
Н·м;
Строим
эпюру крутящих моментов (рис. 4.3). Крутящий
момент, передаваемый вдоль вала от
середины второй шестерни до середины
третьей и первой шестерни:
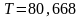 Н·м.
Н·м.
Определяем запас усталостной прочности в сильно нагруженном сечении Б-Б, в котором концентрация напряжений обусловлена шпоночной канавкой и возникают наибольшие моменты.
Коэффициенты запаса прочности по напряжениям кручения определятся по формулам (4.1-4.3).
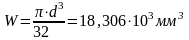
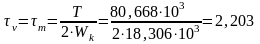
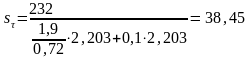
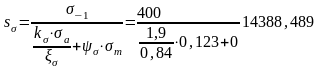
Расчетный коэффициент запаса прочности для сечения А-А
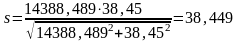 .
.
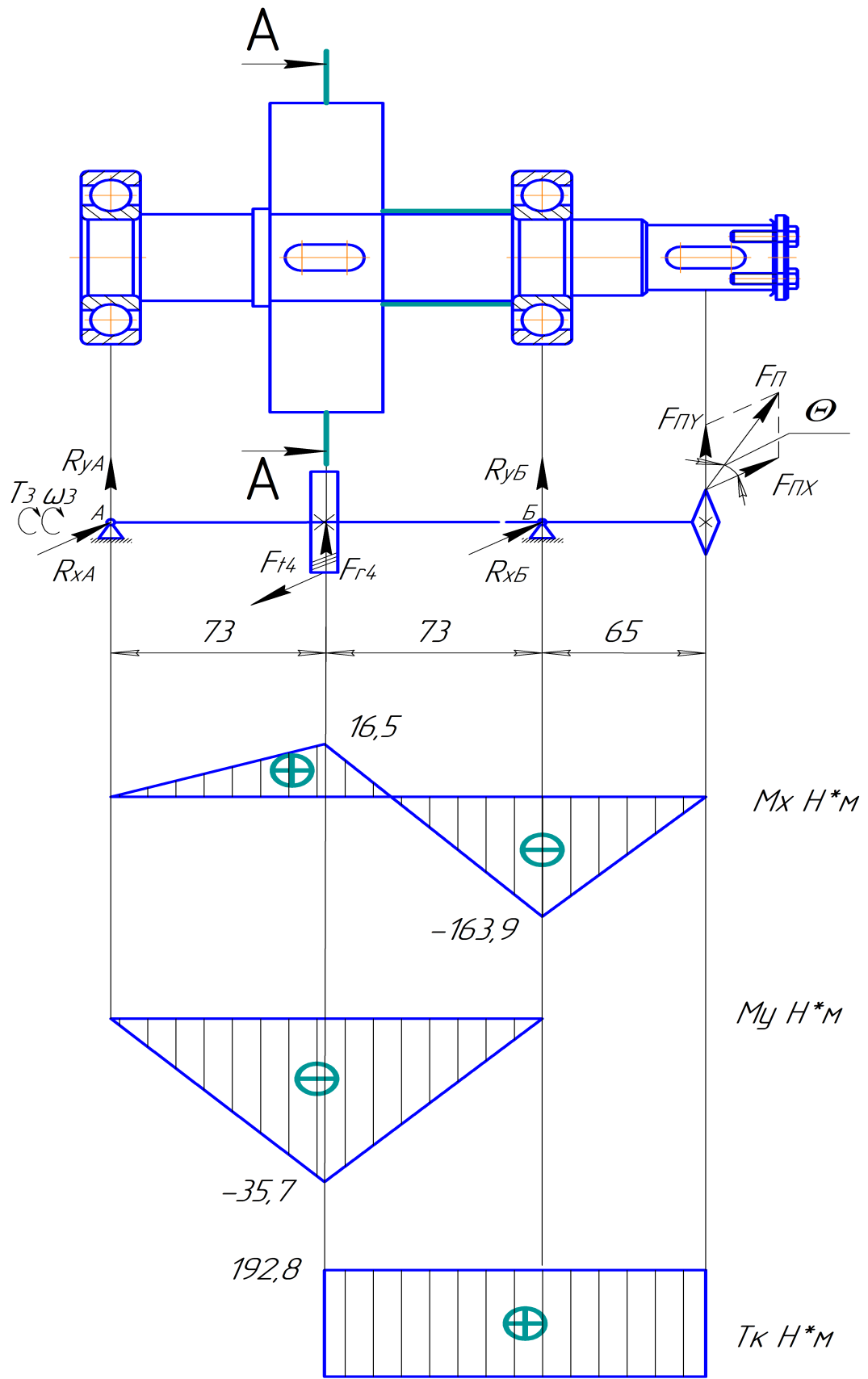
Рисунок 3.3 - Расчетная схема 2-го вала
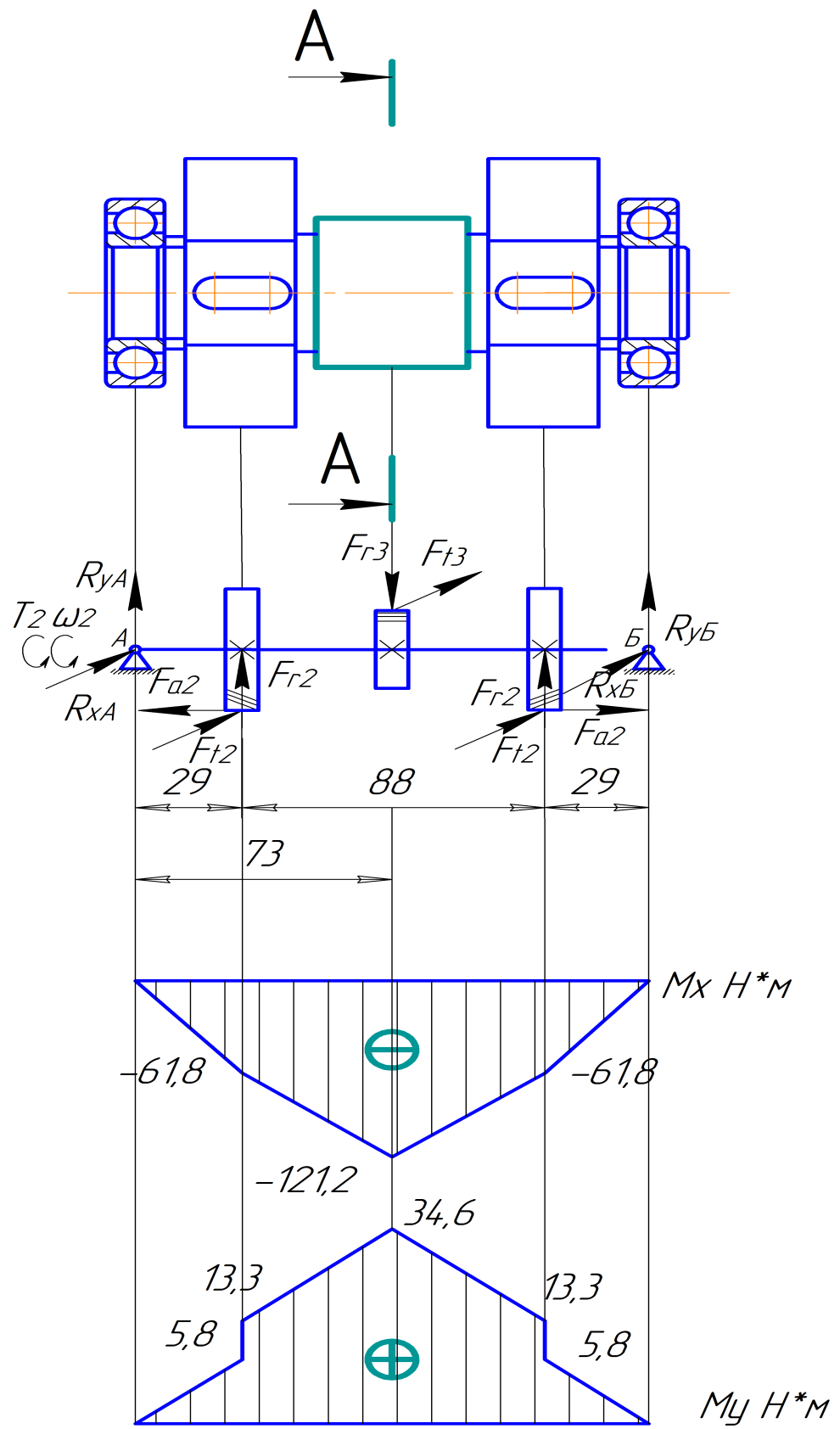
Третий вал.
-
крутящий момент на валу
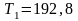 Н·м;
Н·м;
-окружная
сила:
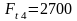 H;
H;
-
радиальная сила:
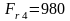 H;
H;
-
осевая сила:
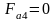 H;
H;
-
нагрузка на вал от цепной передачи:
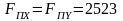 Н.
Н.
Строим эпюры изгибающих моментов в горизонтальной плоскости.
Определяем опорные реакции.
Силовые реакции опор определяем из условия уравновешенности моментов в горизонтальной и вертикальной плоскости относительно каждой из опор.
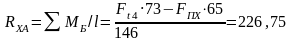 Н
Н
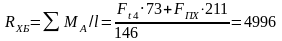 Н
Н
- проверяем правильность определенных реакций:
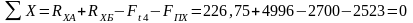
-
строим эпюры изгибающих моментов
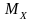 ,
для чего определяем их значение в
характерных сечениях вала:
,
для чего определяем их значение в
характерных сечениях вала:
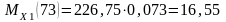 Н·м;
Н·м;
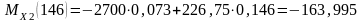 Н·м.
Н·м.
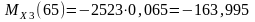 Н·м;
Н·м;
В вертикальной плоскости:
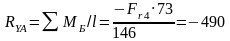 Н
Н
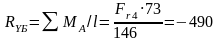 Н
Н
Проверяем правильность определенных реакций:
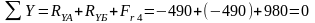
- строим эпюры изгибающих моментов , для чего определяем их значение в характерных сечениях вала:
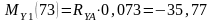 Н·м;
Н·м;
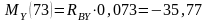 Н·м;
Н·м;
Строим
эпюру крутящих моментов (рис. 4.4). Крутящий
момент, передаваемый вдоль вала от
середины четвёртой шестерни ведущей
звёздочке:
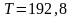 Н·м.
Н·м.
Определяем запас усталостной прочности в сильно нагруженном сечении А-А, в котором концентрация напряжений обусловлена шпоночной канавкой под зубчатое колесо и возникают наибольшие моменты.
Коэффициенты запаса прочности определятся по формулам (4.1-4.3).
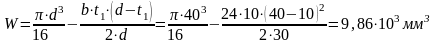
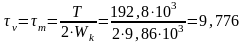
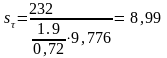
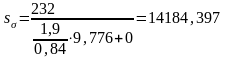 .
.
Расчетный коэффициент запаса прочности для сечение А-А
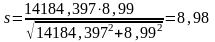 .
.
Рисунок 3.4 - Расчетная схема 3-го вала