3. Расчет прямозубой зубчатой передачи

   1. Выбор материала зубчатых колес и вида термообработки

В качестве материала шестерни и колеса выбираем сталь 40Х, для шестерни с термообработкой улучшение и закалка в ТВЧ, а для колеса – улучшение. Соответственно твердость колеса будет составлять 235-262 НВ (задаем 250 НВ), а для шестерни 269-302 НВ (задаем 280 НВ).

2. Определение допускаемых контактных напряжений для шестерни и колеса

[s]_H=s_H01,2K_HL/S_H,

где s_H01,2 предел контактной выносливости при базовом цикле нагружений, при НВ<350НВ s_H01,2 = 2(НВ)+70,

для шестерни s_H01 = 2280 + 70=630 МПа;

для колеса s_H02= 2250+70=570 МПа.

K_HL – коэффициент долговечности, , где N_НО1,2=(НВ)³, для шестерни N_НО1=(280)³=21952000, N_НО2=(250)³=15625000 циклов. Эквивалентное число циклов нагружения N_НЕ1,2= 60ntc, где n- частота вращения шестерни (колеса), мин^-1; t – срок службы передачи под нагрузкой, ч; с- число зацеплений (число одинаковых зубчатых колес, одновременно находящихся в зацеплении с данной шестерней (колесом) с=1;

n₁= ₁30/=60,2230/3,1415= 575 мин^-1, n₂= ₂30/= 12,0430/3,1415= 115 мин^-1.

t= 113650,8240,6=46252,8 часов.

N_НЕ1= 6057546252,81=1595721600 циклов.

N_НЕ2= 6011546252,81=319144320 циклов.

= 0,49

= 0,61

Так как K_HL в обоих случаях меньше 1, то принимаем K_HL=1.

Коэффициент безопасности принимаем S_H=1,1 (табл.2)

Тогда допускаемые напряжения

₁₌6301/1,1=572,7 МПа,

[s]_H2=5701/1,1=518,2 МПа

Для прямозубых передач расчет ведем по наименьшему из полученных значений, т.е [s]_H=518 МПа.

3. Определение допускаемых напряжений при расчете зубьев на изгиб

[s]_F1,2=s_F0K_F1,2L/S_F1,2

где s_F0 – предел выносливости на изгиб при базовом цикле нагружения, s_F01=600МПа,

s_F02=1,35(НВ_колеса)+100 = 1,35250 + 100= 437,5 МПа;

K_FL1,2 – коэффициент долговечности, , = N_НЕ1,2, соответственно

N_FE1=1595721600 циклов, N_FE2= 319144320 циклов. Так как очевидно, что по расчетам

K_FL1,2<1, то принимаем его равным 1.

S_F1,2 – коэффициент безопасности, для шестерни S_F1=1,7; S_F2=1,65.

Тогда допускаемые напряжения при расчете зубьев на изгиб

Для шестерни [s]_F1= 6001/1,7=352,9 МПа, для колеса [s]_F2= 437,51/1,65=265,2 МПа

4. Определение предельно допускаемых напряжений для шестерни и колеса

При кратковременных перегрузках (расчет на пиковые нагрузки) предельно допускаемые напряжения определяются по эмпирическим зависимостям:

[s]_Hпр1,2=2,86 s_т при твердости £350НВ, [s]_Hпр1=2,86750 = 2145 МПа; [s]_Hпр1=2,86640 = 1830,4 МПа

[s]_Fпр1,2=0,8s_т при твердости £350НВ; [s]_Fпр1=0,8750= 600 МПа; [s]_Fпр1=0,8640= 512 МПа.

5. Определение межосевого расстояния

Определение межосевого расстояния для прямозубых передач выполняется по формуле

где i – передаточное отношение ступени редуктора; Т₂ – вращающий момент на валу колеса, Нмм; y_ba=b₂/a_W – коэффициент ширины зубчатого венца. Для прямозубых передач y_ba =0,125…0,25. Принимаем значения из стандартного ряда по ГОСТ 2185-66 y_ba = 0,16.

K_H определяется по формуле:

K_H=K_HaK_HbK_Hn,

где K_Ha – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями. Для прямозубых передач K_Ha=1.

K_Hb - коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца. При симметричном расположении колес и твердости < 350 НВ K_Hb=1,0…1,15. Принимаем K_Hb=1,05.

K_Hn – коэффициент динамической нагрузки, принимаем K_Hn=1,05.

K_H= 1,01,051,05=1,1025.

a_W=(5+1) 132,0 мм.

Принимаем по ГОСТ 2185-66 ближайшее значение a_W=125 мм.

6. Выбор модуля зацепления

При твердости зубьев шестерни и колеса менее 350 НВ для прямозубых передач рекомендуемый модуль зацепления m = (0,01…0,02) a_W,

m = (0,01…0,02)125 = 1,25…2,5.

Принимаем значение из стандартного ряда по ГОСТ 9563-80 m =2,5.

7. Определение суммарного числа зубьев

z_å=z₁+z₂=2a_W/m

z_å=2125/2,5=100

8. Определение числа зубьев шестерни и колеса

z₁=z_å/(i+1); z₂=z_å-z₁,

z₁=100/(5+1)=17, z₂=100 – 17 = 83.

Уточняем передаточное число i_ред= z_2/ z₁=83/17=4,9.

Отклонение составляет [(4,9-5,0)/5,0]100= 2,0%, что < 2,5% и является допустимым.

9. Проверка межосевого расстояния

Для прямозубых колес a_W= 0,5(z₁+z₂)m,

a_W= 0,5(17+83)2,5=125 мм. Межосевое расстояние соответствует принятому значению.

10. Геометрические размеры зубчатых колес

Делительные диаметры шестерни и колеса

d₁= z₁m, d₂= z₂m

d₁= 172,5= 42,5 мм, d₂= 832,5=207,5 мм.

Проверяем расчетное межосевое расстояние

a_W= 0,5( d₁+ d₂),

a_W = 0,5(42,5+207,5)=125мм.

Диаметры окружностей выступов d_a и впадин d_f зубьев шестерни и колеса

Шестерня

d_a1= d₁+2m, d_f1= d₁-2m;

d_a1= 42,5+22,5= 47,5мм , d_f1= 42,5-22,5= d_f1мм

Колесо

d_a2= d₂+2m, d_f2= d₂-2m;

d_a2= 207,5+22,5= 212,5мм , d_f2= 207,5-22,5=202,5 мм

11. Ширина зубчатого венца колеса и шестерни

b₂=y_baa_W, b₁=b₂+(5…10)мм;

b₂=0,16125=20,0 мм, b₁=20,0 + (5…10) = 25,0…30,0 мм. Принимаем b₂= 20 мм, b₁= 27 мм.

12. Проверка правильности принятых ранее значений размеров заготовок

Диаметр заготовки шестерни

d_заг1»d_a1+(5…10), мм

d_заг1»47,5+(5…10)=52,5…57,5 мм

Диаметр ранее принятой заготовки (d_заг1=125 мм) соответствует полученному результату.

Ширина заготовки зубчатого колеса

s_заг2=5m+(7…10), мм

s_заг2=52,5+(7…10)= 19,5… 22,5 мм

Ширина принятой заготовки (s_заг2=80 мм) соответствует полученному результату.

13. Определение окружной скорости в зацеплении

v=pd₁n₁/(60*1000), м/с.

v= 3,141542,5575/60/1000=1,28 м/с.

14. Назначение степени точности передачи

Для цилиндрической прямозубой передачи при фактической окружной скорости v = 1,28 м/с принимаем 9 класс точности при предельной окружной скорости (табл.5) v_пред=2,0 м/с

15. Уточнение коэффициента нагрузки

K_H=K_HaK_HbK_Hn,

Для прямозубых передач K_Ha=1,0; при y_ba<0,4 симметричном расположении колес и твердости < 350 НВ K_Hb=1,02 (табл.7); K_Hn при окружной скорости 1,28 м/с, степени точности передачи равной 9 и твердости < 350 НВ по табл. 2.9 [2] K_Hn= 1,14

K_H=1,021,01,14=1,16

16. Проверка величины расчетного контактного напряжения

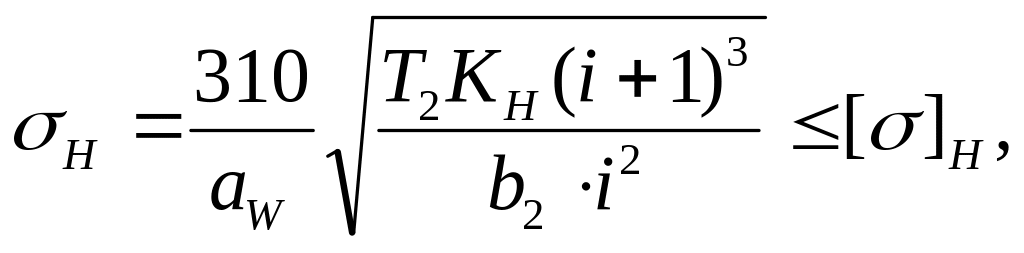
Расчетное контактное напряжение превышает допускаемое на =(_H-[_H])/[_H]100= (574-518)/518100=10,8%, что находится в допускаемом диапазоне отклонений (0,8…1,05[_H])

17. Проверка зубьев на выносливость при изгибе

_F= ,

где Y_F – коэффициент формы зуба, зависящий от числа зубьев, Y_F1=4,025, Y_F2=3,6;

Y_ – коэффициент, учитывающий наклон зубьев. Для прямозубых - Y_=1;

K_FL – коэффициент нагрузки, K_FL = K_F K_F  K_F,

где K_F - коэффициент, учитывающий неравномерность распределения нагрузки между зубьями, для прямозубых - K_F=1; K_F - коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца, при _bd> 0,4 K_F=1,03 (табл.9); K_F - коэффициент динамичности нагрузки, K_F= K_Hn=1,33.

K_FL = 1,01,031,14=1,174

Расчет _F ведем для менее прочного из пары зубчатых колес, т.е. для того, у которого отношение [_F]/ Y_F имеет меньшее значение, шестерня - [_F1]/Y_F1=353/4,025=87,0, колесо [_F2]/ Y_F2=314/3,6=87,2

_F1= =352,9 МПа.

18. Усилия в зацеплении

Окружная сила

F_t= T₁/d_1,

F_t=22,2410³/42,5=523 Н

Радиальная сила

F_r= F_ttg,

где  - стандартный угол равный 20, а tg=0,364;

F_r= 5230,364=190Н

Результаты расчетов основных параметров прямозубой передачи заносим в таблицу

Таблица 1

Основные параметры передачи

Наименование параметра	Обозначение и числовое значение
1. Вращающийся момент на ведомом валу зубчатой передачи, Нм	T2=107,864
2. Угловые скорости валов, рад/с	1=60,22; w2=12,04
3. Межосевое расстояние, мм	aW=125
4. Модуль, мм	m=2,5
5. Число зубьев: шестерни колеса	z1=17 z2=83
8. Диаметр делительный, мм: шестерни колеса	d1=42,5 d2=207,5
9. Диаметр вершин, мм: шестерни колеса	da1=47,5 da2=212,5
10. Диаметр впадин, мм: шестерни колеса	df1=37,5 df2=202,5
11. Ширина зубчатого венца, мм: шестерни колеса	b1=27 b2=20
12. Силы в зацеплении, Н: окружная радиальная	Ft=523 Fr=190