Chainov_Ivashenko_Konstr_dvs / Чайнов Иващенко - Конструирование ДВС

Рис. 8.30. Диаграмма "время сечение" клапана

двигателя. В районе ВМТ в конце такта выпуска и начале такта на полнения впускной и выпускной клапаны на протяжении 1 + 4 уг ла поворота коленчатого вала от крыты. Величину 1 + 4 называют перекрытием клапанов. Благодаря перекрытию клапанов обеспечива ется продувка камеры сгорания и уменьшение тепловой напряжен ности деталей цилиндропоршневой группы, включая головку (крышку) цилиндров и клапаны. Перекрытие клапанов возрастает с увеличением давления наддува.

Кроме геометрических парамет ров клапанов и значений фаз газо распределения, для оценки гидро динамической эффективности ме ханизма газораспределения ис пользуют интегральный параметр "время сечение" А, характеризую щий одновременно с продолжи тельностью открытия также пло щадь проходного сечения клапана,

где F – текущая площадь проход ного сечения клапана; 1, 2 – время начала открытия и закрытия клапа

на, с; Ф – продолжительность от крытия (угол действия) клапана.

Для впускного и выпускного кла панов четырехтактного двигателя со ответственно Фвп = 1 + 180 + 2 и

Фвып = 3 + 180 + 4, а для двухтакт ного двигателя Фвып = 3 + 4.

На рис. 8.30 дана диаграмма "время сечение" клапана. "Время сечение" А равно в соответствую щем масштабе площади под кривой F проходного сечения клапана, со ответствующей рассматриваемому моменту времени (углу поворота коленчатого вала ). Площадь А2 со ответствует значению "время сече ние" при перемещении поршня от ВМТ до НМТ, а площади А1 и А3 – предварению впуска и запаздыва нию закрытия впускного клапана. При неизменных фазах газораспре деления и полном ходе клапана h значение "время сечение" зависит от профиля кулачка. Влияние про филя кулачка при этом оценивают по средней теоретической скорости W ( 30cmFп/iAn (здесь Fп – площадь поршня). Для двухклапанных голо вок W ( для впускного клапана со ставляет 90–150 м/c в случае двига телей с принудительным воспламе нением и 80–110 м/c для дизелей;

при применении б льшего числа клапанов на один цилиндр указан ные скорости можно снизить соот ветственно до 62 и 55 м/c.

8.2. Кулачки. Кинематика

идинамика механизма газораспределения

Одной из важнейших задач, ре шаемых при проектировании меха низма газораспределения с кулачко вым приводом клапанов, является синтез закона движения толкателя. Последнее непосредственно связа но с профилированием кулачков. Существуют различные подходы к получению профиля кулачка при заданных фазах газораспределения и максимальном ходе толкателя или клапана (при непосредственном воздействии кулачка на клапан).

Одна группа методов предусмат ривает предварительное задание конфигурации профиля кулачка, например, образованного дугами окружностей различных радиусов. В основу другой группы методов по ложен заданный закон движения толкателя (клапана). В результате должен быть получен профиль ку лачка, при котором обеспечивается принятый закон с учетом ряда до полнительных условий, в частно сти, допустимых значений положи тельных и отрицательных ускоре ний на различных участках движе ния толкателя (клапана). В послед нее время в связи с повышением быстроходности двигателей и тре бований к механизму газораспреде ления при формировании заданных характеристик двигателя в целом предложены более универсальные численные методы синтеза закона движения толкателя и профиля ку лачка с учетом конструкции МГР. В этом случае достигается увеличение "время сечение" с выполнением на

всем протяжении действия кулачка требований снижения интенсивно сти колебательных процессов в ме ханизме газораспределения, в том числе ограничения высших произ водных от перемещения толкателя по углу поворота распределительно го вала, что в свою очередь обеспе чивает более гладкое изменение ус корения толкателя по углу поворота кулачка. Высокая надежность МГР является обязательным условием при любом варианте его выполне ния. Важным требованием является обеспечение технологичности изго товления кулачка.

На рис. 8.31 показан симметрич ный кулачок, при использовании которого обеспечивается постоян ный подъем клапана на участке СС. Окружность радиуса rн, от которой в точке А начинается рабочий участок кулачка, называется начальной или делительной. Если тыльную сторону кулачка выполнять по делительной окружности rн, т.е. проектировать так называемый идеальный клапан ный механизм, то при работе двига теля вследствие теплового расшире ния деталей механизма возможен от ход клапана от седла и нарушение уплотнения камеры сгорания. Для того, чтобы предотвратить разгерме тизацию камеры сгорания, когда по

Рис. 8.31. Профиль кулачка

ложение толкателя (клапана) соот ветствует тыльной стороне кулачка, в клапанном механизме между кла паном и тыльной стороной кулачка предусмотрен регулируемый тепло вой зазор s. При работе двигателя на различных режимах зазор будет из меняться в зависимости от теплового состояния деталей МГР, а при ниж нем расположении распределитель ного вала от теплового состояния корпуса и головки (крышки) цилин дров двигателя. В последнем случае, например, у двигателей воздушного охлаждения тепловой зазор при ра боте может оказаться больше, чем в холодном состоянии вследствие то го, что тепловое расширение цилин дров и их головок превысит тепловое расширение клапанов.

При верхнем расположении рас пределительного вала тепловой за зор в холодном состоянии больше, чем при работающем двигателе. Так как профилировать целесооб разно идеальный кулачок, то для учета тепловой деформации радиус тыльной стороны кулачка rк умень шают на значение теплового зазора s относительно радиуса начальной окружности: rк = rн s. При верх нем расположении распредели тельного вала и непосредственном действии кулачка на клапаны через цилиндрические толкатели на ав томобильных двигателях в холод ном состоянии зазор составляет 0,08–0,20 мм для впускных и 0,10– 0,35 мм для выпускных клапанов. Зазор регулируется с помощью на бора регулировочных шайб.

В случае нижнего расположения распределительного вала, наличия штанги и коромысла зазор между стержнем клапана и бойком коро мысла или стержнем клапана и ре гулировочным болтом принимают 0,3–0,35 мм. Повышенный зазор отрицательно влияет на работу ме

ханизма газораспределения, приво дя к стукам, повышенному изнаши ванию подвижных сочленений и се дел клапанов. Зазор в холодном со стоянии должен обеспечить мини мальный зазор на работающем дви гателе. Для устранения нежелатель ных явлений, связанных с тепловым зазором, применяют гидравлические толкатели.

Важное значение имеет скорость посадки клапана на седло. Работа механизма газораспределения счи тается удовлетворительной, если скорость посадки клапанов состав ляет 0,2–0,4 м/с. Переход от точки А на рабочей части кулачка к точке А0 на радиусе rк выполняют по пара боле или спирали Архимеда.

С учетом переходных участков АА0 действительный угол профиля

кулачка 2&д = 2&0 + 2&s, где угол &s соответствует участку сопряжения

окружности радиуса rк (точка А0) с началом активного профиля кулач ка (точка А).

В поршневых двигателях приме няют кулачки различного профиля. В ряде случаев профиль кулачков образуется дугами окружностей. При этом кулачки могут быть с выпук лым профилем (выпуклые кулачки), с вогнутым профилем (вогнутые ку лачки), а также тангенциальные (рис. 8.32, б). Выпуклый кулачок (рис. 8.32, а) может работать с толка

Рис. 8.32. Профили кулачков, образованных дугами:

а – выпуклого; б – тангенциального; в – во гнутого

Рис. 8.33. Построение выпуклого профиля ку лачка

телем любого типа. Вогнутый кула чок (рис. 8.32, в) не используется для работы с плоским толкателем. В ос новном он предназначен для работы c роликовым толкателем.

На рис. 8.33 показано построе ние симметричного выпуклого профиля кулачка, образованного тремя дугами окружностей двух ра диусов R и rг. Рассмотрен идеаль ный кулачок без так называемого верхнего "выстоя" толкателя, нали чие которого считается нежела тельным для большинства автомо бильных двигателей.

В четырехтактных двигателях угол поворота распределительного вала & = /2 (здесь – угол пово рота коленчатого вала). Поэтому для кулачка впускного клапана

2&0 вп = ( 1 + 180 + 2)/2, а для ку

=

= ( 3 + 180 + 4)/2. В двухтактных двигателях для кулачка выпускного

клапана 2&0 = 3 + 4. Выбирают радиус начальной окружности rн =

= (1,5–2)hт. Из центра О проводят начальную окружность и на верти кальной оси на расстоянии от цен

тра О, равном rн + hт (максималь ный подъем толкателя hт считается известным), получают точку С про филя. Откладывая от линии ОС угол &0, получают точку А на на чальной окружности. На продол жении линии АО на расстоянии R от точки А наносят центр О1, из ко торого радиусом R проводят линию АВ. Радиус R выбирают равным в пределах (10–18)hт. Выбрав радиус головки rг, из точки О2, лежащей на линии ОС, проводят дугу окружно сти rг. Точка В является точкой со пряжения окружностей радиусов R и rг. Правая сторона профиля (рис. 8.33) симметрична левой. При заданных hт и &0 из трех параметров (rн, R, rг) независимыми являются только два. Так, при задании пара метров R и rн радиус головки

(R rн )[(rн hт )cos &0 rн ]

(8.3)

Если заданным является радиус головки rг (обычно rг > 1,5–2 мм), то

где d = rн + hт rг – расстояние ме жду точками О и О2.

С уменьшением радиуса R уменьшается и rг. Увеличение rг ве дет к увеличению R, достигающему

R = при rг max. В этом случае кула чок превращается в тангенциаль

ный:

При дальнейшем увеличении rг получается кулачок с вогнутым

профилем, участок АВ которого очерчивается дугой окружности ра диуса R1( , проведенный из центра O1( , лежащего с противоположной стороны по отношению к центру О1 (рис. 8.33) на расстоянии rн + R1( от центра О. Уравнения перемещения hтx, скорости vтx и ускорения jтx тол кателя для участков АВ и ВС будут различными.

Для выпуклого кулачка в случае плоского толкателя (рис. 8.34) для участка АВ путь толкателя при по вороте кулачка на угол &, соответ ствующий отрезку А1А2,

hтx (R rн )(1 cos &). (8.6)

Скорость vтx и ускорение jтx полу чаются дифференцированием урав нения (8.6) по времени:

Максимальный угол &max, при ко тором толкатель еще находится на первом участке профиля в точке В,

&max arcsin[dsin &0 (R rг )]. (8.9)

Для участка ВС (рис. 8.34, б) при определении пути толкателя удобно ввести вспомогательный угол Φ = &0&. Окончательно путь, скорость и ускорение толкателя на участке ВС определяются выражениями:

Как следует из приведенных за висимостей, в точке В происходит смена знака ускорения толкателя с положительного на отрицательный (рис. 8.35). Эта особенность свой ственна всем кулачкам, профили

Рис. 8.35. Изменение перемещения hтх, скоро сти vтх и ускорения jтх толкателя при выпуклом профиле кулачка

которых образованы дугами окруж ностей, и является их общим не достатком, отрицательно влияю щим на работу звеньев МГР, осо бенно при увеличении частоты вра щения двигателей. Скачок ускоре ния толкателя получается меньше при использовании кулачка, очер ченного пятью дугами трех радиу сов. В этом случае вместо одного скачка ускорения получаются два, существенно меньших (штриховая линия на рис. 8.35). Однако интен сивность возбуждаемых при этом колебаний может даже повыситься.

При применении плоского тол кателя следует определить мини мальный размер rmin его тарелки из условия, что линия контакта кулач ка шириной b и тарелки в точке В полностью расположена в пределах круга радиуса rmin. При эксцентрич ном расположении кулачка отно сительно оси толкателя со смеще нием е размер тарелки толкателя должен быть больше rmin, опреде ляемого по формуле,

В случае применения роликово го толкателя зависимости для рас чета пути, скорости и ускорения толкателя приведены в табл. 8.3.

На рис. 8.36 показаны диаграм мы пути толкателя hтх для различ ных профилей кулачков при одина ковых значениях hт и &0. Кривые пе ремещения для разных профилей мало отличаются между собой. Не сколько большие различия имеют кривые ускорений. Обычно счита ют, что при выпуклом профиле зна чения положительных ускорений на участке АВ больше, но при этом значения отрицательных ускорений на участке ВС меньше, что облегча ет работу пружины. Однако при сравнении значений ускорений сле дует указывать значения параметров кулачков, для которых выполнены сравнительные расчеты. Если при нять одинаковыми угловую ско рость распределительного вала р, угол &0, радиусы R, rн и , то поло жительное ускорение при вогнутом профиле кулачка оказывается вы ше, чем при выпуклом профиле. При выборе профиля, образованно го дугами окружностей, имеет зна чение и его технологичность. Так, тангенциальный кулачок прост, а кулачок с вогнутым профилем наи более сложен в изготовлении. Об

Рис. 8.36. Кривые перемещения hтх для раз личных профилей кулачков:

1 – выпуклого; 2 – вогнутого; 3 – тангенци ального

317

8.3. Формулы для расчета перемещения hтx, скорости vтх и ускорений jтх роликового толкателя при профилях кулачков, описанных дугами окружностей (трех радиусов)

щим недостатком всех профилей, образованных дугами окружностей, является наличие скачка ускорений, что приводит к ударам в МГР, от скокам клапана при посадке на сед ло, усилению колебаний.

Отмеченные явления начинают усиленно проявляться при частоте вращения вала двигателя 1500– 2000 мин 1 и более. При этом дей ствительное перемещение клапана может значительно отклоняться от перемещения, определенного по формулам (8.6); (8.10); (8.14); (8.18); (8.22) и (8.26) вследствие резкого изменения сил инерции и податливости элементов МГР. По этому в быстроходных двигателях взамен кулачков, образованных ду гами окружностей, применяют ку лачки, спрофилированные по за данному закону движения клапана, так называемые "безударные" ку лачки.

Применяемые в современных быстроходных двигателях законы движения толкателя hтх обеспечива ют непрерывность кривой ускоре ний jтх и относительно плавное из менение усилий в звеньях МГР при работе двигателя.

В качестве примера безударного кулачка, обеспечивающего отсутст вие разрывов кривой ускорения в течение всего периода 2&0 действия кулачка, может служить кулачок Курца. При синтезе кулачка перво начально задается кривая ускоре ний jтх (рис. 8.37). На участке сбега Ф0 ускорение толкателя изменяется по закону косинуса. Рабочий уча сток кривой ускорения включает половину синусоиды (участок Ф1), четверть синусоиды (участок Ф2, где ускорение становится отрицатель ным), дугу квадратичной параболы (участок Ф3). Кривые скорости vтх и перемещения hтх толкателя получа ются интегрированием кривой ус

Рис. 8.37. Диаграммы пути, скорости и ускоре ния толкателя при кулачке Курца

корения. Отсчитывая угол поворота кулачка & от начала соответствую щего участка и обозначая индекса ми 0, 1, 2, 3 принадлежность теку щего угла, перемещения, скорости и ускорения рассматриваемому уча стку, используют следующие кине матические зависимости для "без ударного" кулачка. При этом приве денная скорость v(тx vтx p , а при веденное ускорение jт(x = jтx 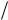2p . Индексами "н" и "к" обозначены на чало и конец участка. На участке сбега кулачка (0 < & < Ф0)