2. Определение передаточного числа привода и его ступеней

Общее передаточное число привода

u = n₁/n_рм = 950/97 = 9,79

принимаем для конической передачи u₁ = 3,15, тогда для открытой пе-

редачи

u₂ = u/u₁ = 9,79/3,15 = 3,11

2. Определение силовых и кинематических параметров привода

Числа оборотов валов и угловые скорости:

n₁ = n_дв = 950 об/мин ₁ = 950π/30 = 99,5 рад/с

n₂ = n₁/u₁ = 950/3,15 = 302 об/мин ₂= 302π/30 = 31,6 рад/с

n₃ = n₂/u₂ = 302/3,11 = 97 об/мин ₃= 97π/30 = 10,2 рад/с

Фактическое значение скорости грузовой цепи

v = πDn₃/6·10⁴ = π·275·97/6·10⁴ = 1,397 м/с

Отклонение фактического значения от заданного

δ = (1,40 – 1,397)100/1,4 = 0,2% < 4%

Полученное значение намного меньше допускаемого

Мощности передаваемые валами:

P₁ = P_трη_мη_пк = 3230·0,98·0,995 = 3150 Вт

P₂ = P₁η_зпη_пк = 3150·0,97·0,995 = 3040 Вт

P₃ = P₂η_опη_пс = 3040·0,93·0,99 = 2800 Вт

Крутящие моменты:

Т₁ = P₁/₁ = 3150/99,5 = 31,7 Н·м

Т₂ = 3040/31,6 = 96,2 Н·м

Т₃ = 2800/10,2 = 274,5 Н·м

Результаты расчетов сводим в таблицу

Таблица 2.3.

Вал	Число оборо­тов об/мин	Угловая ско­рость Рад/сек	Мощность кВт	Крутящий момент Н·м
Вал электродвигателя	950	99,5	3,230	32,5
Ведущий редуктора	950	99,5	3,150	31,7
Ведомый редуктора	302	31,6	3,040	96,2
Рабочий привода	97	10,2	2,800	274,5

3. Выбор материалов зубчатых передач и определение допускаемых напряжений

Принимаем, согласно рекомендациям [1c.52], сталь 45:

шестерня: термообработка – улучшение – НВ235÷262 [1c.53],

колесо: термообработка – нормализация – НВ179÷207.

Средняя твердость зубьев:

НВ_1ср = (235+262)/2 = 248

НВ_2ср = (179+207)/2 = 193

Допускаемые контактные напряжения:

[σ]_H = K_HL[σ]_H0,

где K_HL – коэффициент долговечности

K_HL = (N_H0/N)^1/6,

где N_H0 = 1·10⁷ [1c.55],

N = 573ωL_h = 573·31,6·20,5·10³ = 38,3·10⁷.

Так как N > N_H0, то К_HL = 1.

[σ]_H1 = 1,8HB+67 = 1,8·248+67 = 513 МПа.

[σ]_H2 = 1,8HB+67 = 1,8·193+67 = 414 МПа.

[σ]_H = 0,45([σ]_H1 +[σ]_H2) = 0,45(513+414) = 417 МПа.

Допускаемые напряжения изгиба:

[σ]_F = K_FL[σ]_F0,

где K_FL – коэффициент долговечности

Так как N > N_F0 = 4·10⁶, то К_FL = 1.

[σ]_F01 = 1,03HB₁ = 1,03·248 = 255 МПа.

[σ]_F02 = 1,03HB₂ = 1,03·193 = 199 МПа.

[σ]_F1 = 1·255 = 255 МПа; [σ]_F2 = 1·199 = 199 МПа.

4. Расчет закрытой конической передачи

Внешний делительный диаметр колеса

,

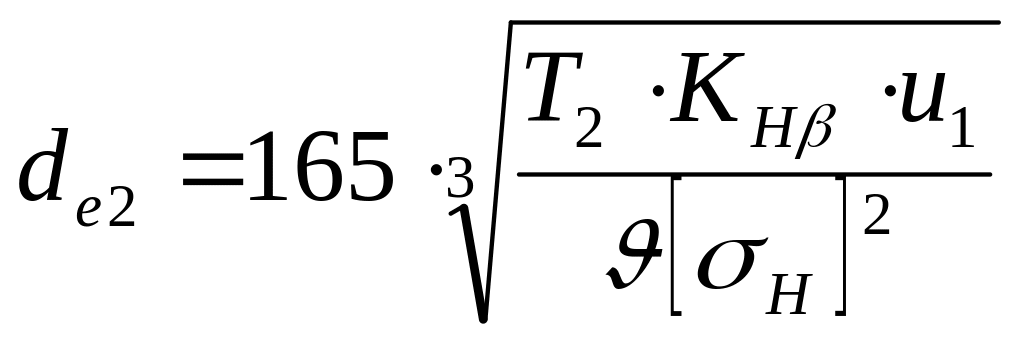где K_HB = 1,1 – коэффициент, учитывающий распределение нагрузки по ширине венца для колес с круговыми зубьями

= 1,85 – коэффициент вида конических колес

d_e2 = 165[(96,210³1,13,15)/(1,85·417² )]^1/3= 167 мм

Принимаем по ГОСТ 12289–766 d_e2 = 160 мм

Углы делительных конусов

сtg₁ = u₁ = 3,15  ₁ = 17,61°,

₂ = 90^o – ₁ = 90^o – 17^o36’ = 72,39^o.

Внешнее конусное расстояние R_e и длина зуба b

R_e = d_e2/(2sinδ₂) = 160/(2sin72,39°) = 84 мм,

b = y_bRR_e

где y_{bR = 0,285 – коэффициент ширины колеса}

b = 0,285×84 = 24 мм

Внешний окружной модуль

m_te = 14T₂K_Fβ /( _Fd_e2b[σ]_F

где _А = 1 – для колес с круговыми зубьями,

К_Fβ = 1,08 – для колес с круговыми зубьями

m_te = 14·96,2·10³·1,08/(1,0·160·24·199) = 1,90 мм.

принимаем m_te = 1,9 мм

Число зубьев колеса и шестерни

z₂ = d_e2/m_te = 160/1,9 = 84

z₁ = z₂/u₁ = 84/3,15 = 27

Фактическое передаточное число конической передачи

u₁ = z₂/z₁ = 84/27 = 3,11

По таблице 4.6 [1c.68] находим коэффициент смещения для шестерни и колеса х_n1 = 0,23; х_n2 = -0,23

Диаметры шестерни и колеса

d_e1 = m_tez₁ = 1,90·27 = 51,3 мм

Диаметры вершин зубьев

d_ae1=d_e1+ 1,64(1+x_n1)m_tecos δ₁ = 51,3+1,64(1+0,23)1,9·cos17,61°=54,95 мм

d_ae2 = d_e2 + 1,64(1 – x_n2)m_tecos δ₂ =

= 160 + 1,64(1 + 0,23)1,90·cos72,39° =161,16 мм

Диаметры впадин зубьев

d_fe1=d_e1–1,64(1,2–x_n1)m_tecos δ₁ =

= 51,3–1,64(1,2–0,23)1,9·cos17,61° = 48,42 мм

d_fe2 = d_e2 – 1,64(1,2 + x_n2)m_tecos δ₂ =

= 160 – 1,64(1,2 – 0,23)1,9·cos72,39° =159,08 мм

Средние делительные диаметры

d₁ ≈ 0,857d_e1 = 0,857·51,3 = 43,96 мм

d₂ ≈ 0,857d_e2 = 0,857·160 = 137,12 мм

Силы действующие в зацеплении:

окружная

F_t= 2T₂/d₂ = 2×96,2×10³/137,12 = 1403 Н

радиальная для шестерни, осевая для колеса

F_r1 = F_a2 = F_tγr = 1403·0,208 = 292 H

где γ_r – коэффициент радиальной силы

γ_r = (0,44cosδ₁ – 0,7sinδ₁) = 0,44cos17,61° – 0,7sin17,61° = 0,208

осевая для шестерни, радиальная для колеса

F_a1= F_r2 = F_tγa = 1403·0,80 =1122 H

где γ_а – коэффициент осевой силы

γ_а = (0,44sinδ₁ + 0,7cosδ₁) = 0,44sin17,61° + 0,7cos17,61° = 0,80

Средняя окружная скорость.

V = ω₂d₂/210³ = 31,6·137,12/210³ = 2,2 м/с.

Принимаем 7 – ую степень точности

Расчетное контактное напряжение

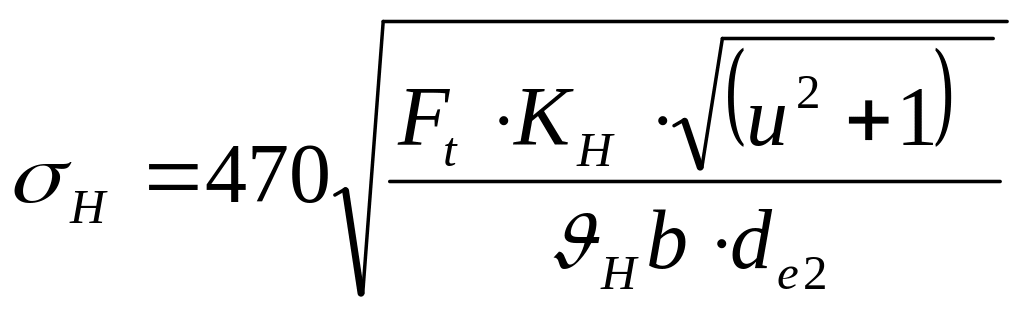
где К_Н – коэффициент нагрузки

K_H = K_HαK_HβK_Hv =1,0×1,05·1,1 =1,155

K_Hα = 1,0 – коэффициент учитывающий неравномерность распределения нагрузки между зубьями [1c.69]

K_Hβ = 1,1–коэффициент учитывающий неравномерность распределения нагрузки по ширине венца [1c.65]

K_Hv = 1,05 – динамический коэффициент [1c62]

σ_Н = 470{14031,155[(3,15²+1)]^1/2/(1,85·24160)}^1/2 = 408 МПа

Недогрузка (417 – 408)100/417= 2,2 % < 10%,

Проверяем напряжения изгиба зубьев шестерни и колеса

σ_F2 = Y_F2Y_βF_tK_FαK_FβK_Fv/( _Fbm_te)

σ_F1 =σ_F2Y_F1/Y_F2

где Y_F – коэффициент формы зуба, зависящий от эквивалентного числа зубьев

z_v= z/(cosd·cos³β)

β = 35° - угол наклона зубьев

z_v1 = 27/(cos17,61°·cos³35°) = 51,5 → Y_F1 = 3,55

z_v2 = 84/(cos72,39°·cos³35°) = 505 → Y_F2 = 3,63

Y_β = 1 – коэффициент учитывающий наклон зуба

K_Fα = 1,0 – коэффициент учитывающий неравномерность распределения нагрузки между зубьями [1c.69]

K_Fβ = 1,0 – для прирабатывающихся зубьев

К_Fv = 1,09 – коэффициент динамичности [1c62]

σ_F2 = 3,63·1,0·1403·1,0·1,0·1,09/(1,0·24·1,9) = 119 МПа < [σ]_F2

σ_F1 = 119·3,55/3,63 = 117 МПа < [σ]_F1

Так как расчетные напряжения σ_H < [σ_H] и σ_F < [σ]_F, то можно утверждать, что данная передача выдержит передаваемую нагрузку и будет стабильно работать в нормальных условиях весь срок службы.