
- •Выбор электродвигателя и кинематические расчеты.
- •Выбор материала и расчеты допускаемых контактных напряжений.
- •Расчет цилиндрической зубчатой передачи.
- •Эскизное проектирование.
- •Конструирование подшипниковых узлов.
- •Расчет шпоночного соединения.
- •Расчет подшипника на долговечность.
- •Выбор смазки редуктора.
- •Список используемой литературы.
Эскизное проектирование.
Предварительные диаметры валов.
Диаметры вала и вала – шестерни будем определять по следующим зависимостям [1]:
- для быстроходного вала, т.е. для вала – шестерни
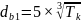 ,
(35)
,
(35)
- для тихоходного
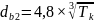 ,
(36)
,
(36)
где
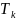 - крутящий момент;
- крутящий момент;
Подставляя числовые значения в формулы (35) и (36) получим следующее:
- для быстроходного вала
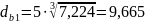
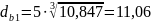 мм
мм
Согласовывая
диаметр вала с диаметром вала
электродвигателя подшипника назначаем
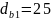 мм.
мм.
- для тихоходного вала
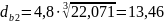
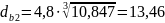 мм
мм
Также согласуя
диаметр тихоходного вала с внутренним
диаметром подшипника выбираем
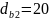 мм.
мм.
Определю ширину шестерни по формуле [1]:
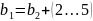 .
(37)
.
(37)
Подставим значение
ширины колеса
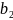 и получим следующее значение:
и получим следующее значение:
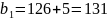
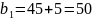 мм
мм
Предварительный выбор подшипников.
Используя рекомендации и таблицу [1, 18.28] из учебника назначаем для вала и для вала – шестерни шарикоподшипники радиально-упорные однорядные следующих серий:
Для вала выбираем
подшипник средней серии 46305 с параметрами
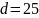 мм,
мм,
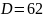 мм,
мм,
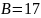 мм.
мм.
Для вала – шестерни выбираем также подшипник средней серии 46305 с параметрами мм, мм, мм
где
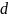 - внутренний диаметр подшипника;
- внутренний диаметр подшипника;
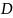 - наружный диаметр
подшипника;
- наружный диаметр
подшипника;
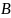 – ширина колец
подшипника.
– ширина колец
подшипника.
Конструирование подшипниковых узлов.
Определение схемы параметров установки подшипников.
Назначаю схему установки радиально-упорных подшипников в распор.
Радиальная реакция подшипника считается приложенной к оси вала в точке пересечения с ней нормали, проведенной через середину контактной площадки. Для радиальных подшипников эта точка располагается на середине ширины подшипника. Для радиально-упорных подшипников расстояние а между этой точкой и торцом подшипника может быть определено графически или аналитически по следующим формуле [1]:
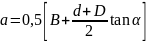 ,
(38)
,
(38)
где α – это угол, который предварительно назначаем из таблицы /1, 18.32/ равным 120.
Подставив числа (38) получим следующие значение расстояния а:
для подшипника серии 46305
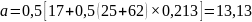 мм
мм
Далее определяем расстояние между точками приложения радиальных реакций при установке радиально-упорных подшипников по схеме в распор по формуле [1]:
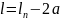 ,
(39)
,
(39)
где –
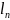 расстояние между торцами наружных колец
подшипников;
расстояние между торцами наружных колец
подшипников;
Подставим числа
в формулу (39) найдем значение
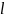 :
:
для вала-колеса
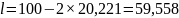 мм
мм
Определение радиальных реакций в подшипниках и построение эпюр крутящих моментов.
Будем определять реакции отдельно в горизонтальной и вертикальной плоскостях для вала колеса и для вала шестерни.
Расчет в горизонтальной плоскости для вала-колеса.
На Рисунке 1 представлена расчетная схема вала-колеса.
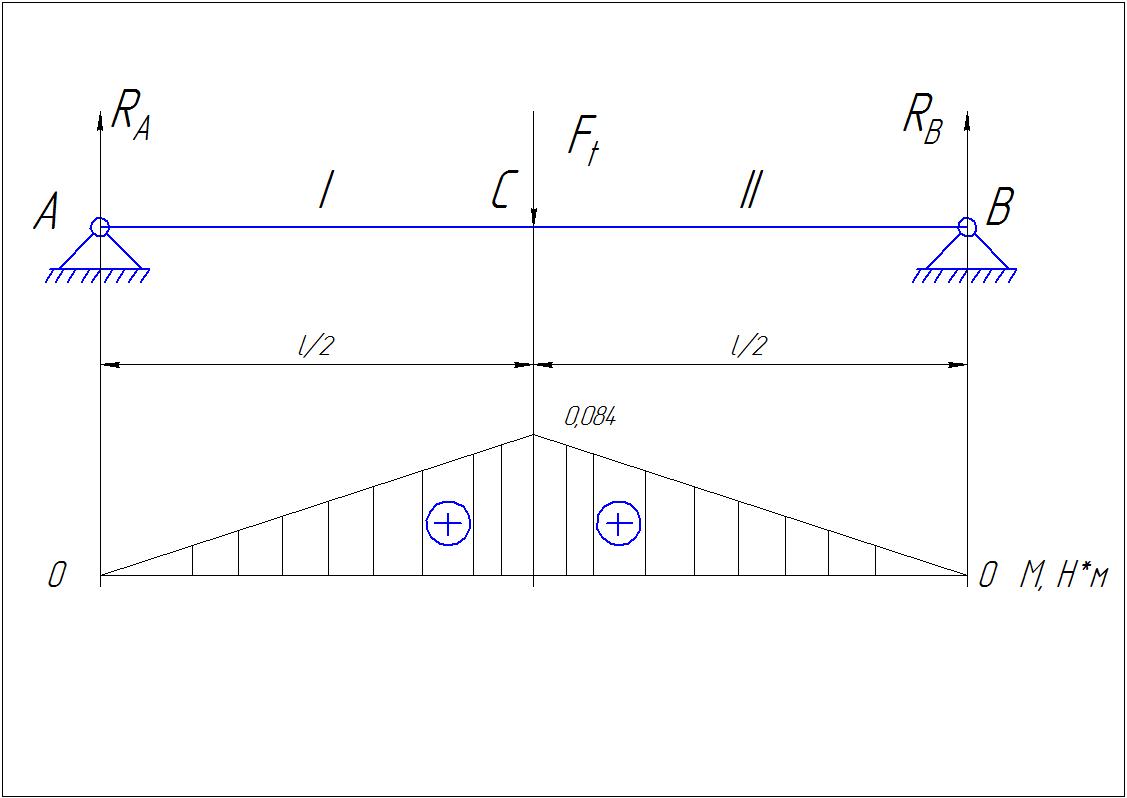
Рисунок 1 - Расчетная схема тихоходного вала в горизонтальной плоскости.
Определяем реакции RB и RA из условия равновесия.
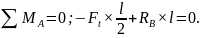 (40)
(40)
Отсюда получим значение RB
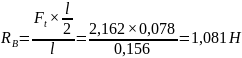 (41)
(41)
Отсюда получим значение RA
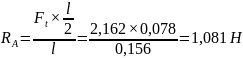 (42)
(42)
Выполним проверку вычисления реакции по следующему соотношению:
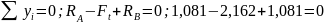
Проверка выполняется, значит реакции найдены верно.
Далее определим изгибающие моменты на валу:
МАI=0
H м.
м.
МСI=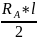 =1,081
× 0,078 = 0.084 H
м
=1,081
× 0,078 = 0.084 H
м
МСII = 0,084 H м.
МВII
=
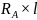 -
-
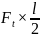 =1,081
× 0,156 – 2,162 × 0,078 = 0 Н
м
=1,081
× 0,156 – 2,162 × 0,078 = 0 Н
м
Эпюра изгибающих моментов для вала в горизонтальной плоскости представлена на рисунке 1.
Расчет в вертикальной плоскости для вала-колеса.
На рисунке 2 представлена расчетная схема нагружения вала.
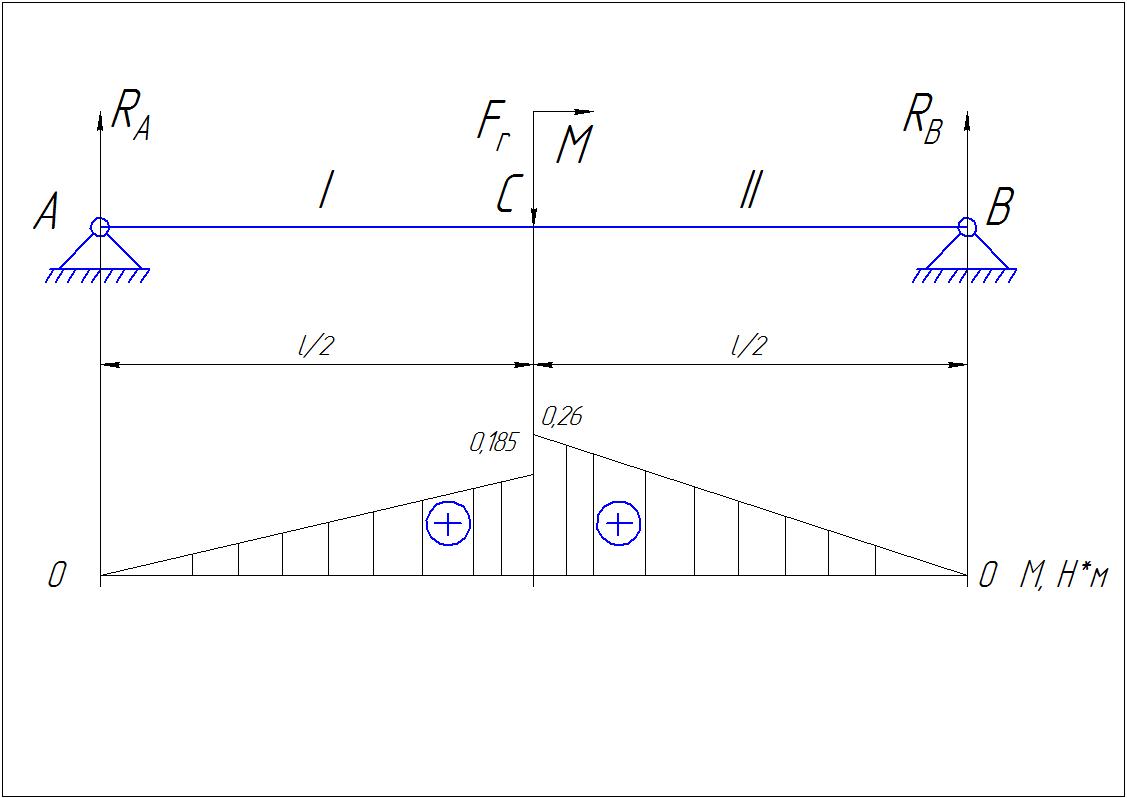
Рисунок 2 – Расчетная схема тихоходного в вертикальной плоскости.
Определяю значение момента М и реакции RB и RA:
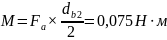 . (42)
. (42)
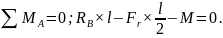
Отсюда найдем значение RB:
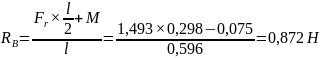 (43)
(43)
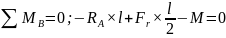
Отсюда найдем значение RA
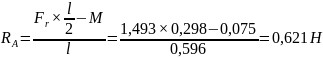 (44)
(44)
Выполню проверку вычисления реакций, применив следующее выражение:
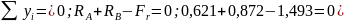
Проверка выполняется, значит реакции найдены верно.
Определю изгибающие моменты на валу:
МАI = 0 H м.
MCI
=
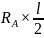 =
0,621 × 0,298 = 0,185 H
м
=
0,621 × 0,298 = 0,185 H
м
МСII
= М + RA×
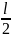 = 0,075 + 0,185 = 0,26 Н
м
= 0,075 + 0,185 = 0,26 Н
м
МBII =RA×l–Ft × +М = 0 Н м.
Эпюра изгибающих моментов для вала в вертикальной плоскости представлена на рисунке 2.
Далее определяю суммарный изгибающий момент по формуле [1]:
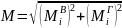 ,
(45)
,
(45)
где
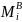
– момент в вертикальной плоскости;
– момент в вертикальной плоскости;
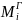 – момент в
горизонтальной плоскости;
– момент в
горизонтальной плоскости;
Вычислим суммарные изгибающие моменты:
для вала-колеса
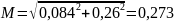 Н*м
Н*м
Далее рассчитываю
эквивалентный момент
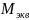 на валах по формуле [1]:
на валах по формуле [1]:
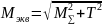 ,
(46)
,
(46)
где М∑ – суммарный момент.
Подставим числовые значения в формулу (45) и получим следующее:
Для вала-колеса
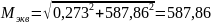 Н
м
Н
м
Уточнение расчетов валов.
Произведем расчет валов по формуле [1]:
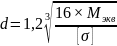 .
(47)
.
(47)
В числовом выражении соотношение примет следующий вид:
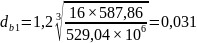 м
= 31 мм
м
= 31 мм
Данные значения диаметров валов не превышает ранее принятых, значит предварительный расчет валов выполнен верно.
