4 Расчет закрытой червячной передачи

Межосевое расстояние

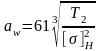= 61(113,810³/130²)^1/3 =115 мм

принимаем а_w = 125 мм

Основные геометрические параметры передачи

Модуль зацепления:

m = (2,01,7)a_w/z₂,

где z₂ – число зубьев колеса.

При передаточном числе 12,5 число заходов червяка z₁ = 4, тогда число зубьев колеса:

z₂ = z₁u = 412,5 = 50,0

m = (2,01,7)125/50 = 3,74,3 мм,

принимаем m = 4,0 мм.

Коэффициент диаметра червяка:

q = (0,2120,25)z₂ = (0,2120,25)50 =10,612,5

принимаем q = 12,5

Коэффициент смещения

x = a/m – 0,5(q+z₂) = 125/4,0 – 0,5(12,5+50) = 0

Фактическое значение межосевого расстояния:

a_w = 0,5m(q+z₂+2x) = 0,54,0(12,5+50 – 20) = 125 мм

Делительный диаметр червяка:

d₁ = qm =12,504,0 = 50,0 мм

Начальный диаметр червяка d_w1 = m(q+2x) = 4,0(12,5-2·0) = 50,0 мм

Диаметр вершин витков червяка:

d_a1 = d₁+2m = 50,0+45,0 = 58 мм.

Диаметр впадин витков червяка:

d_f1 = d₁ – 2,4m = 50,0 – 2,44,0 = 40,0 мм.

Длина нарезной части червяка:

b₁ = (10+5,5|x|+z₁)m + C = (10+5,50+4)4,0+0 = 56 мм.

при х < 0  С = 0.

Делительный угол подъема линии витка:

 = arctg(z₁/q) = arctg(4/12,5) =17,74

Делительный диаметр колеса:

d₂ = mz₂ = 4,050 = 200,0 мм.

Диаметр выступов зубьев колеса:

d_a2 = d₂+2m(1+x) = 200,0+24,0(1-0) = 208,0 мм.

Диаметр впадин зубьев колеса:

d_f2 = d₂ – 2m(0,857 – x) = 200,0 – 24,0(0,857 + 0) = 190 мм.

Наибольший диаметр зубьев колеса:

d_am2 = d_a2+6m/(z₁+2) = 208,0+64,0/(4+2) = 2118,6 мм.

Ширина венца колеса:

b₂ = 0,315a_w = 0,315125 = 40 мм.

2.5. Фактическое значение скорости скольжения

v_s = u₂d₁/(2000cos) = 12,5∙7,8550,0/(2000cos17,74) = 2,58 м/с

2.6. Коэффициент полезного действия червячной передачи

 = (0,950,96)tg/tg(+)

где  = 2,0º - приведенный угол трения [1c.74].

 = (0,950,96)tg17,74/tg(17,74+2,0º) = 0,86.

2.7. Силы действующие в зацеплении

Окружная на колесе и осевая на червяке:

F_t2 = F_a1 = 2Т₂/d₂ = 2113,810³/200,0 = 1138 H.

Радиальная на червяке и колесе:

F_r1 = F_r2 = F_t2tg = 1138tg20 = 414 H.

Окружная на червяке и осевая на колесе:

F_t1 = F_a2 = 2M₁/d₁ = 2118,610³/50,0 = 460 H.

2.8. Расчетное контактное напряжение

_Н = 340(F_t2K/d₁d₂)^0,5,

где К – коэффициент нагрузки.

Окружная скорость колеса

v₂ = ₂d₂/2000 = 7,85200,0/2000 = 0,8 м/с

при v₂ < 3 м/с  К = 1,0

_Н = 340(11381,0/50,0200,0)^0,5 = 115 МПа,

недогрузка (130 – 115)100/130,0 =118,6% <15%.

Расчетное напряжение изгиба для зубьев колеса

_F = 0,7Y_F2F_t2K/(b₂m),

где Y_F2 – коэффициент формы зуба колеса.

Эквивалентное число зубьев колеса:

z_v2 = z₂/(cos)³ = 50/(cos17,74)³ = 57,9  Y_F2 = 1,41.

_F = 0,71,4111381,0/(404,0) = 7,0 МПа.

Условие _F < []_F = 22 МПа выполняется.

Так как условия 0,85<_H < 1,05[_H] и _F < [_F] выполняются, то можно утверждать, что устойчивая работа червячной закрытой пере­дачи обеспечена в течении всего срока службы привода.

5 Расчет открытой зубчатой передачи

Выбор материалов зубчатой передачи

Принимаем, согласно рекомендациям [1c.52], сталь 45:

шестерня: термообработка – улучшение – НВ235÷262 [1c.53],

колесо: термообработка – нормализация – НВ179÷207.

Средняя твердость зубьев:

НВ_1ср = (235+262)/2 = 248

НВ_2ср = (179+207)/2 = 193

Допускаемые контактные напряжения:

[σ]_H = K_HL[σ]_H0,

где K_HL – коэффициент долговечности

K_HL = (N_H0/N)^1/6,

где N_H0 = 1·10⁷ [1c.55],

N = 573ωL_h = 573·2,07·24,5·10³ = 2,20·10⁷.

Так как N > N_H0, то К_HL = 1.

[σ]_H2 = 1,8HB+67 = 1,8·193+67 = 414 МПа.

Допускаемые напряжения изгиба:

[σ]_F = K_FL[σ]_F0,

где K_FL – коэффициент долговечности

Так как N > N_F0 = 4·10⁶, то К_FL = 1.

[σ]_F01 = 1,03HB₁ = 1,03·248 = 255 МПа.

[σ]_F02 = 1,03HB₂ = 1,03·193 = 199 МПа.

[σ]_F1 = 1·255 = 255 МПа.

[σ]_F2 = 1·199 = 199 МПа.

Внешний делительный диаметр колеса

,

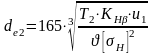где K_Hβ = 1,0 – коэффициент, учитывающий распределение нагрузки по ширине венца для прямозубых колес

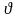= 1,0 – коэффициент вида конических колес (колеса прямозубые)

d_e2 = 165[(41410³1,05,0)/(1,0·414² )]^1/3= 410 мм

Принимаем по ГОСТ 6636–69 d_e2 = 400 мм [1c.326]

Углы делительных конусов

сtg₁ = u₁ = 5,0  ₁ = 11,31°,

₂ = 90^o – ₁ = 90^o – 11,31° = 78,69^o.

Внешнее конусное расстояние R_e и длина зуба b

R_e = d_e2/(2sinδ₂) = 400/(2sin78,69°) =204 мм,

b = y_bRR_e

где y_bR = 0,285 – коэффициент ширины колеса

b = 0,285×204 = 58 мм

Внешний окружной модуль

m_e = 14T₂K_Fβ /( _Fd_e2b[σ]_F)

где _F = 0,85 – для колес с прямыми зубьями,

К_Fβ = 1,0 – для колес с прямыми зубьями

m_e = 14·414·10³·1,0/(0,85·400·58·199) = 1,87 мм.

В открытых конических передачах из-за повышенного изнашивания зубьев рекомендуется увеличить модуль на 30%. Исходя из этого принимаем m_e = 2,50 мм.

Число зубьев колеса и шестерни

z₂ = d_e2/m_e = 400/2,5 = 160

z₁ = z₂/u₁ = 160/5,0 = 32

Фактическое передаточное число конической передачи

u₁ = z₂/z₁ = 160/32 = 5,00

отклонение δ = 0%

По таблице 4.6 [1c.71] находим коэффициент смещения для шестерни и колеса х_е1 = 0,33; х_е2 = -0,33

Диаметры шестерни и колеса

d_e1 = m_ez₁ = 2,5·32 = 80 мм

Диаметры вершин зубьев

d_ae1 = d_e1+ 2(1+x_е1)m_ecos δ₁ = 80 +2(1+0,33)2,5·cos11,31° = 86,52 мм

d_ae2 = d_e2 + 2(1–x_е2)m_ecos δ₂ = 400+2(1+0,33)2,5·cos78,69° =401,30 мм

Диаметры впадин зубьев

d_fe1 = d_e1–2(0,857–x_е1)m_ecos δ₁ = 80,0–2(0,857–0,33)2,5cos11,31°= 75,73 мм

d_fe2 = d_e2 – 2(0,857+x_е2)m_ecos δ₂ = 400–2(0,857–0,33)2,5cos78,69° =399,15 мм

Средние делительные диаметры

d₁ ≈ 0,857d_e1 = 0,857·80,0 = 68,6 мм

d₂ ≈ 0,857d_e2 = 0,857·400 = 342,8 мм

Силы действующие в зацеплении:

окружная

F_t3 = F_t4 = 2T₃/d₂ = 2×414×10³/342,8 = 3066 Н

радиальная для шестерни, осевая для колеса

F_r3 = F_a4 = 0,36F_tcosδ₁ = 0.36·3066cos11,31° = 1082 H

осевая для шестерни, радиальная для колеса

F_a3= F_r4 = 0,36F_tsinδ₁ = 0,36·3066·sin11,31° = 216 H

Средняя окружная скорость.

V = ω₂d₁/210³ = 7,85·68,6/210³ = 0,26 м/с.

Принимаем 7 – ую степень точности.

Расчетное контактное напряжение

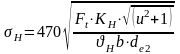
где К_Н – коэффициент нагрузки

K_H = K_HαK_HβK_Hv =1,0×1,04·1,0 =1,04

K_Hα = 1,0 – коэффициент учитывающий неравномерность распределения нагрузки между зубьями [1c.69]

K_Hβ = 1,0–коэффициент учитывающий неравномерность распределения нагрузки по ширине венца [1c.65]

K_Hv = 1,04 – динамический коэффициент [1c62]

σ_Н = 470{30661,04[(5,0²+1)]^1/2/(1,0·58400)}^1/2 = 393 МПа

Недогрузка (414 – 393)100/414= 5,1 %

Допускаемая недогрузка 10%,

Проверяем напряжения изгиба зубьев шестерни и колеса

σ_F2 = Y_F2Y_βF_tK_FαK_FβK_Fv/( _Fbm_e)

σ_F1 =σ_F2Y_F1/Y_F2

где Y_F – коэффициент формы зуба, зависящий от эквивалентного числа зубьев z_v= z/cosd

z_v1 = 32/cos11,31° = 32,6 → Y_F1 = 3,53

z_v2 = 160/cos79,69° = 894 → Y_F2 = 3,63

Y_β = 1 – коэффициент учитывающий наклон зуба

K_Fα = 1,0 – коэффициент учитывающий неравномерность распределения нагрузки между зубьями [1c.69]

K_Fβ = 1,0 – для прирабатывающихся зубьев

К_Fv = 1,07 – коэффициент динамичности [1c62]

σ_F2 = 3,63·1,0·3066·1,0·1,0·1,07/(1,0·58·2,5) = 82 МПа < [σ]_F2

σ_F1 = 82·3,53/3,63 = 80 МПа < [σ]_F1

Так как расчетные напряжения 0,9[σ]_H < σ_H < 1,05[σ_H] и σ_F < [σ]_F, то можно утверждать, что данная передача выдержит передаваемую нагрузку и будет стабильно работать в нормальных условиях весь срок службы.

Нагрузки валов редуктора

Силы действующие в зацеплении червячной передачи

Окружная на колесе и осевая на червяке:

F_t2 = F_a1 = 1138 H.

Радиальная на червяке и колесе:

F_r1 = F_r2 =414 H.

Окружная на червяке и осевая на колесе:

F_t1 = F_a2 = 460 H.

Консольная сила от муфты действующая на быстроходный вал

F_м = 100·Т₁^1/2 = 100·118,6^1/2 = 339 Н

Консольная силы действующие на тихоходный вал

окружная

F_t3 = 3066 Н

радиальная

F_r3 =1082 H

осевая

F_a3 = 216 H

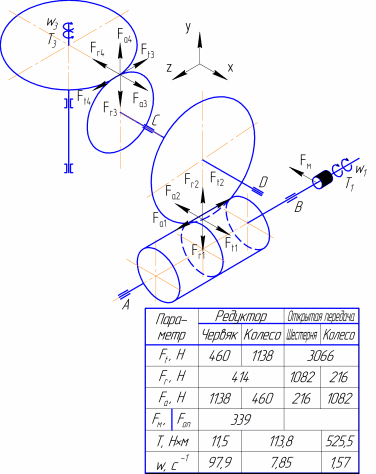
Рис. 6.1 – Схема нагружения валов червячного редуктора