1. Кинематический расчет

1. Подбор электродвигателя

Для выбора электродвигателя определяют требуемую его мощность и частоту вращения.

Потребляемую мощность (кВт) привода определяют по формуле:

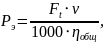
где F_t - окружная сила, F_t=10 кН; v – скорость ленты, v=0,8 м/с; _общ – общий КПД кинематической цепи.

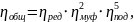
где _зуб – КПД зубчатой передачи, _ред = 0,98⁴; _муф – КПД муфты, _муф =0,98; _под – КПД подшипника, _под =0,99.

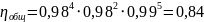
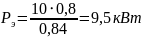
По таблице 24.9 [2, c. 417] выбирается электродвигатель АИР 132m4/1395 с мощностью P_э=11,0 кВт.

2. Определение частот вращения и вращательных моментов на валах

Определяется частота вращения привода nпр (мин-1)

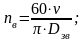
где D – диаметр звездочки, D=318 мм.

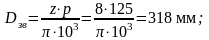
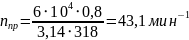
Определяется передаточное число редуктора u_ред

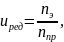
где n_э – частота вращения электродвигателя, n_э=1395 мин^-1.

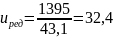
Передаточные числа редуктора.

u_1-2 =6 – передаточное отношение редуктора.

u_2-3 =5,6 – передаточное отношение цепной передачи.

n_в – частота вращения выходного вала:

В итоге

Приводной вал:

• мощность .

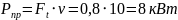• частота вращения 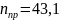об/мин.

• угловая скорость 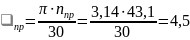c^-1.

• крутящий момент 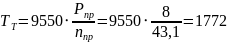Нм

Тихоходный вал редуктора:

• мощность

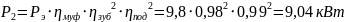
• частота вращения 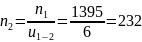об/мин.

• угловая скорость 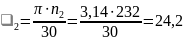c^-1.

• крутящий момент 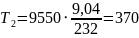Нм

Быстроходный вал редуктора:

• мощность .

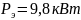• частота вращения 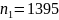об/мин.

• угловая скорость 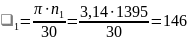c^-1.

• крутящий момент 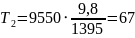Нм

3. Расчет быстроходной цилиндрической зубчатой передачи.

Исходные данные:

Т₂ = 370 Нм — вращающий момент на колесе;

n₂ = 232 об/мин — частота вращения колеса;

u = 6 — передаточное число;

3.1. Материалы колеса и шестерни.

В качестве материала для цилиндрического колеса применяем ст.45. Применяем т.о. колеса – улучшение, твердость НВ 235…262.

Механические свойства: _T = 640 МПа.

В качестве материала для шестерни используем ст.45. Применяем т.о. шестерни – улучшение, твердость НВ 269…302.

Механические свойства: _Т = 750 МПа.

3.2. Допускаемые напряжения.

Вычисляем до­пускаемые контактные напряжения.

Для колеса:

допускаемые контактные напряжения:

[]_H = 1,8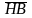 +67 = 1,8248,5+67=514 МПа;

допускаемые напряжения на из­гиб: []_F = 1,03 = 1,03248,5=256 МПа;

предельные допускаемые напряже­ния:

[]_Hmax = 2,8_Т = 2,8640 = 1792 МПа;

[]_Fmax = 2,74 =2,74248,5 = 680,9 МПа;

Для шестерни:

допускаемые контактные напряжения:

[]_H = 1,8 +67 = 1,8285,5+67=581 МПа;

допускаемые напряжения на из­гиб: []_F = 1,03 = 1,03285,5=294 МПа;

предельные допускаемые напряже­ния:

[]_Hmax = 2,8_Т = 2,8750 = 2100 МПа;

[]_Fmax = 2,74 =2,74285,5 = 782,3 МПа;

4. 3.3 Межосевое расстояние:

,

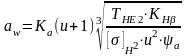где K_a – коэффициент межосевого расстояния; К_а = 4300 – для шевронных колес;

_a – коэффициент ширины венца по межосевому расстоянию: для шевронных передач _a = 0,4.

Коэффициент концентрации нагрузки для прирабатывающихся колес при переменном режиме работы К_H = К⁰_H(1-X)+X1,05, где

К⁰_H - начальный коэффициент концентрации нагрузки; принимаем в зависимости от коэффициента _d=0,5_a(u+1)=0,50,4(6,3+1)=1,46К⁰_H =1,85.

X – коэффициент режима нагрузки; для среднего нормального режима нагружения X=0,5 (средний нормальный режим нагружения наиболее характерен для транспортных машин).

Таким образом К_H = 1,85 (1-0,5)+0,5=1,425 >1,05.

Эквивалентный мо­мент на колесе Т_НЕ2 = К_НдТ₂ ,

где 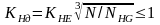— коэффициент долговечности.

Здесь: К_НЕ — коэффициент эквивалентности, зависящий от режима нагружения (при среднем нормальном режиме нагружения К_НЕ=0,56);

N_HG=( )³=23271176,38 — ба­зовое число циклов нагружений.

N – суммарное число циклов.

В итоге коэффициент циклов .

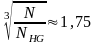Следовательно К_Нд=1,750,56=0,98

Следовательно эквивалентный мо­мент на колесе Т_НЕ2 = 365 Н.

Межосевое расстояние в итоге:

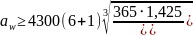
Принимаем значение межосевого расстояния a_w=130 мм.

3.4 Предварительные основные размеры колеса.

- делительный диаметр:

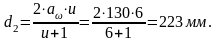
- ширина колеса: ,

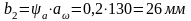где _а – коэффициент ширины колеса, _а=0,2.

принимаем стандартное значение b₂ = 26 мм.

3.5 Модуль передачи

Модуль передачи:

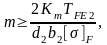
где коэффициент K_m принимают для косозубых колес: K_m =5,2.

Т_FE=К_FдТ₂—эквивалентный момент на колесе,

где 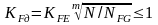— коэффициент долговечности. Здесь N_FG=410⁶— базовое число циклов. При N10⁸ принимаем K_Fд=1,0.

Т.о. эквивалентный момент на колесе Т_FE=Т₂=238,3 Н.

Модуль принимает значение:

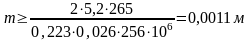
Принимаем модуль передачи равным m = 1,25 мм.

3.6 Суммарное число зубьев и угол наклона.

Минимальный угол наклона зубьев косозубых колес _min = 10;

Суммарное число зубьев

z_=2 a_wcos_min /m.

z_=2130cos 10 /1,25 = 205

Определяем действительное значение угла

 = arccos (z_m / 2a_w).

 = arccos (2051,25 / 2130) = 9,45.

3.7 Число зубьев шестерни и колеса.

Число зубьев шестерни

z₁ = z_/(u±l)z_1min.

Для косозубых колес z_1min = 17cos³ = 13;

z₁ = 205/(6+l) = 29 > z_1min.

Число зубьев колеса: z₂ = z_ - z₁ = 209 – 29 = 176.

3.8 Фактическое передаточное число

Фактическое передаточное число u_ф= z₂/ z₁ = 176 / 29 6.

Отклонение от заданного передаточного числа не превышает допускаемых 4%.

3.9 Диаметры колес.

Дели­тельные диаметры, d:

шестерни d₁ =z₁m/cos = 291,25 / cos 9,45 = 36,7 мм;

колеса d₂ =2a_w- d₁ = 2130 – 36,7 = 223,3 мм.;

Диаметры окружностей вершин d_a и впадин d_f зубьев:

d_a1=d₁ +2(1 +x₁ - y)m = 36,7 + 211,25 = 39,2 мм;

d_f1=d₁ - 2(1,25 - x₁)m= 36,7 - 21,251,25 = 33,65 мм;

d_a2=d₂ +2(1 +x₂ - y)m= 223,3 + 211,25 = 225,7 мм;

d_f2=d₂ - 2(1,25 – x₂)m= 223,3 - 21,251,25 = 220,1 мм;