
МММСС (От Кувыркина Г.Н.) / 88
.pdf
31
Известно, что фундаментальная система решений однородной системы линейных алгебраических уравнений (СЛАУ) (63) относительно n неизвестных zj, j = 1, n, матрица которой с элементами ψij имеет ранг r, состоит из n − r линейно независимых решений. Таким
решениям соответствуют ровно n − r независимых степенных одночленов Πq, q = 1, n−r, размерность которых равна единице, поскольку показатели степени zj любого другого степенного одночлена Π, будучи решениями СЛАУ (63), можно представить линейной комбинацией решений из фундаментальной системы, а это означает, что Π можно представить произведением степеней Πq.
Ранг r прямоугольной матрицы размера k×n с элементами ψij, называемой матрицей размерностей, при n > k может принять наибольшее возможное значение, равное числу k ее строк. В этом случае из n основных параметров можно составить n = n − k безразмерных комбинаций, т. е. степенных одночленов, что и является одним из утверждений основной теоремы теории размерностей — Π-теоремы. Но в общем случае r 6 k, и поэтому формулировку Π-теоремы следует уточнить: имеющую физический смысл зависимость между n основными параметрами, характеризующими изучаемый процесс, можно представить в виде зависимости между n = n − r их независимыми безразмерными комбинациями, где r — ранг матрицы размерностей, элементами которой являются показатели в выражениях вида (61) для размерности этих параметров.
Из этой теоремы также следует, что при помощи безразмерных комбинаций — критериев подобия — можно привести к безразмерному виду любую зависимость между n параметрами, имеющую физический смысл. Действительно, если такая зависимость содержит слагаемые, то их размерность должна быть одинаковой, а аргументы показательных, тригонометрических, обратных тригонометрических и других функций (кроме, может быть, степенных) должны быть безразмерными. Поэтому такую зависимость путем элементарных операций можно представить в безразмерном виде.
В большинстве прикладных задач r = k. Однако возможны случаи, когда r < k, что заставляет при использовании теории размерностей проверять ранг матрицы размерностей. Применим теорию размерностей к процессу тепломассопереноса в вязкой несжимаемой жидкости.
При фиксированной форме области, имеющей характерный размер L, и характерных значениях скорости v0, температуры T0, давления p0 и объемной концентрации C0, входящих в условия однозначности, в число основных размерных параметров для рассматриваемого процесса тепломассопереноса необходимо также включить время t, модуль |w| вектора ускорения и теплофизические свойства жидкости: плотность ρ, кинематическую вязкость νD, температуропроводность a(T ), концентрационную диффузию D(C) и темпе-
(T )
ратурный коэффициент объемного расширения αV . Пространственные координаты xi (i = 1, 2, 3) и проекции vi вектора скорости на оси координат, а также T , p и C можно не включать в основные параметры, поскольку их можно привести к безразмерному виду xi = xi/L, vi = vi/v0, θ = T/T0, p = p/p0 и C = C/C0 непосредственно при помощи уже выбранных основных параметров, имеющих с ними одинаковые размерности, образовав так называемые безразмерные симплексы, которые следует включить в безразмерные зависимости на заключительной стадии их формирования.
Таким образом, общее число рассматриваемых определяющих размерных параметров, которые должны войти в независимые определяющие критерии подобия, составляет n = 12. Элементы матрицы размерностей для этих параметров представлены в табл. 1.
Таблица 1
Единица |
|
|
|
|
|
|
Параметр |
|
|
|
|
||
измерения |
L |
v0 |
T0 |
p0 |
C0 |
t |
|
|w| |
ρ |
νD |
a(T) |
D(C) |
αV(T) |
м |
1 |
1 |
0 |
−1 |
−3 |
0 |
|
1 |
−3 |
2 |
2 |
2 |
0 |
кг |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
с |
0 |
−1 |
0 |
−2 |
0 |
1 |
−2 |
0 |
−1 |
−1 |
−1 |
0 |
|
К |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
−1 |
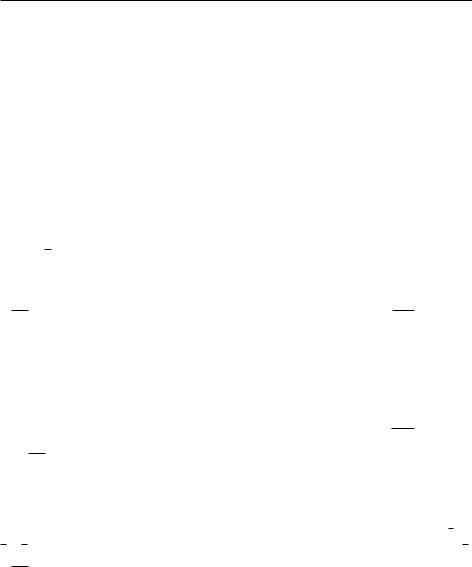
32
Перестановкой столбцов в этой таблице соответствующую ей прямоугольную матрицу можно привести к ступенчатому виду. Расположение элементов в такой матрице представлено в табл. 2.
Таблица 2
Единица |
|
|
|
|
|
|
Параметр |
|
|
|
|
||
измерения |
L |
ρ |
t |
T0 |
v0 |
p0 |
|
C0 |
|w| |
νD |
a(T) |
D(C) |
αV(T) |
м |
1 |
−3 |
0 |
0 |
1 |
−1 |
−3 |
1 |
2 |
2 |
2 |
0 |
|
кг |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
с |
0 |
0 |
1 |
0 |
−1 |
−2 |
|
0 |
−2 |
−1 |
−1 |
−1 |
0 |
К |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
−1 |
Определитель, составленный из первых четырех столбцов ступенчатой матрицы, равен −1, т. е. отличен от нуля, следовательно, ранг матрицы размерностей r = k = 4. Поэтому из n = 12 размерных определяющих параметров в соответствии с Π-теоремой можно составить n = n −k = 8 независимых безразмерных комбинаций. Показатели zj степеней этих параметров в выражении для каждой безразмерной комбинации в форме (62) удовлетворяют однородной СЛАУ вида (63), матрица которой является матрицей размерностей.
Для нахождения фундаментальной системы решений СЛАУ указанный определитель примем в качестве базисного минора матрицы размерностей, поэтому неизвестные zj (j =
= 1, 4) будут базисными. Выразим их через свободные неизвестные zj, j = 5, 12, используя ступенчатый вид матрицы размерностей:
z1 = −z5 − 2z6 − z8 − 2z9 − 2z10 − 2z11, z2 = −z6 − z7,
z3 = z5 + 2z6 + 2z8 + z9 + z10 + z11, z4 = z12.
Значения свободных неизвестных в правых частях этих равенств можно выбрать произвольно. Выбирая эти значения последовательно, так, чтобы одно из них равнялось единице, а остальные — нулю, получаем из записанных равенств значения zj (j = 1, 12) показателей степени, с которыми определяющие параметры входят в безразмерные комбинации Πm
(m = 1, 8) вида (62). Эти значения представлены в табл. 3.
При помощи этой таблицы запишем выражения для независимых безразмерных комби-
наций: Π1 = v0t/L, Π2 = p0t2/(L2ρ), Π3 = C0/ρ, Π4 = |w|t2/L, Π5 = νDt/L2, Π6 = a(T )t/L2, Π7 = D(C)t/L2, Π8 = α(T )T0. Из них лишь Π1 и Π6 совпадают с входящими в (60) числами
гомохронности Ho и Фурье Fo соответственно. Но несложно установить, что Π2/Π21 = Eu, Π1/Π5 = Re, Π6/Π1 = Pe, Π5/Π6 = Pr, Π5/Π7 = Sc, Π4Π8/(Π5Π6) = Ra, Π4Π3/(Π5Π7) = RaC ,
Π6/Π5 = Lu. Важно подчеркнуть, что в качестве аргументов безразмерных функций θ, C, p и vi, i = 1, 2, 3, которые удовлетворяют (60), наряду с безразмерными координатами xi следует использовать ровно восемь независимых безразмерных комбинаций в виде Πm (m =
= 1, 8) или столько же полученных из них независимых критериев подобия.
Отметим, что из полученных безразмерных комбинаций Πm можно также построить
еще ряд определяющих критериев подобия, используемых при исследовании движения
жидкости и процессов тепломассопереноса в ней. Так, Π4/Π21 = |w|L/v02 = Fr называют
числом Фруда, характеризующим соотношение сил тяжести и инерционных сил. Влияние
числа Фруда обычно существенно в случае, когда вес жидкости, вытесненной объемом
твердого тела, сопоставим с весом тела (например, при движении воздушного шара
или дирижабля). Если движение жидкости у поверхности твердого тела вызвано лишь
объемными силами, то обычно не удается выбрать в качестве характерной скорости v0
какое-либо определенное значение. Тогда вместо чисел Рейнольдса и Фруда при анализе
подобия процессов используют число Галилея Ga = Re2Fr = |w|L3/νD2 = Π4/Π25, которое

|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комби- |
|
|
|
|
|
|
Параметр |
|
|
|
|
||
нация |
L |
ρ |
t |
T0 |
v0 |
p0 |
|
C0 |
|w| |
νD |
a(T) |
D(C) |
αV(T) |
Π1 |
−1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
Π2 |
−2 |
−1 |
2 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
Π3 |
0 |
−1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
Π4 |
−1 |
0 |
2 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
Π5 |
−2 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
Π6 |
−2 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
Π7 |
−2 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
Π8 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
служит мерой соотношения сил тяжести и вязкого трения. |
Если в двух характерных |
||||||||||||
точках области, занятой жидкостью, известны значения температур T1 и T2, то можно |
|||||||||||||
ввести число Грасгофа Gr = α(T ) |
| |
T1 |
− |
T2 |
| |
Ga = |
|w|L3 |
| |
T1 |
− |
T2 |
| |
. В более общем случае |
V |
|
|
|
νD2 |
|
|
|
||||||
объемные силы могут возникнуть за счет неоднородности жидкости, что приводит к изменению ее плотности в рассматриваемой области. Тогда используют число Архимеда
|
|
|
|
. |
|
|
|
|
|
− |
ρ1 |
|
|
νD2 |
|
− ρ1 |
|
Ar = 1 |
|
ρ2 |
|
Ga = |
|w|L3 |
1 |
ρ2 |
, где ρ1 и ρ2 — плотность жидкости в двух характерных |
|
|
|
|
|
|
|
|
|
точках этой области
1.6. Некоторые модели пограничного слоя
При обтекании неподвижного твердого тела потоком вязкой жидкости в силу эффекта прилипания скорость ее частиц на поверхности тела равна нулю, а по мере удаления в глубь потока по направлению нормали к поверхности постепенно возрастает, стремясь к некоторому значению в обтекающем потоке. Прилегающую к поверхности тела область течения, в которой происходит наиболее существенное изменение скорости, называют пограничным слоем. Под толщиной этого слоя понимают расстояние от обтекаемой поверхности, на котором с обусловленной точностью завершается изменение скорости жидкости, хотя формально возмущение поля скоростей, вызванное торможением частиц жидкости на поверхности тела, распространяется во всей области течения.
В зависимости от режима течения различают ламинарный и турбулентный пограничные слои. Помимо пристенного пограничного слоя, который образуется при обтекании твердого тела, возникают так называемые свободные пограничные слои при движении в неподвижной жидкости струй или вихревых следов, срывающихся с поверхности обтекаемого тела. Здесь ограничимся рассмотрением математических моделей (ММ) ламинарного пристенного пограничного слоя в случае установившегося течения несжима-
емой жидкости.
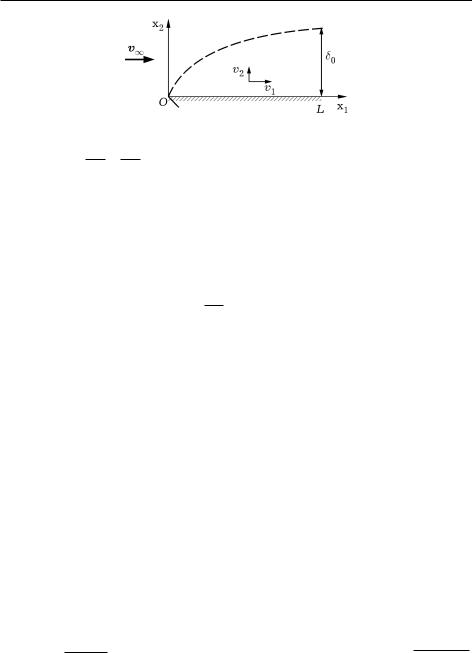
Если вдали от обтекаемого тела течение жидкости является безвихревым, то такой режим течения сохраняется и за пределами пограничного слоя, в котором течение носит вихревой характер. Рассмотрим установившееся обтекание тонкой пластины потоком жидкости, имеющим вдали от пластины вектор скорости v∞, совпадающий с положительным направлением оси Ox1 прямоугольной системы координат Ox1x2x3 (рис. 0.10). В этом случае течение жидкости будет плоским, а уравнение (50) переноса завихренности при-
мет вид
|
∂W3 |
|
∂W3 |
∂2W3 |
|
∂2W3 |
|
|
|
v1 |
|
+ v2 |
|
= νD |
|
+ νD |
|
, |
(64) |
∂x1 |
∂x2 |
∂x12 |
∂x22 |
||||||
где v1 и v2 — проекции вектора v(x1,x2) скорости на оси Ox1 и Ox2 соответственно,
удовлетворяющие уравнению неразрывности в виде ∂v1 + ∂v2 = 0; νD — кинематическая
∂x1 ∂x2
34
Рис. 0.10
вязкость; W3 = ∂v2 − ∂v1 — единственная отличная от нуля проекция на ось Ox3 вектора
∂x1 ∂x2
завихренности, перпендикулярного в данном случае плоскости x1Ox2.
Левая часть (64) характеризует интенсивность конвективного переноса вихрей, правая часть — интенсивность их диффузионного переноса. Толщина δ пограничного слоя зависит от взаимодействия этих механизмов переноса. Оценим роль отдельных слагаемых в (64), введя масштабы входящих в них величин: v∞ = |v∞| для v1, т. е. v1 = O(v∞), где O(·) — символ порядка величины; W0 для W3, L как характерный размер стенки в направлении оси Ox1 и δ0 как масштаб, характеризующий порядок величины δ, т. е. δ = O(δ0). Из уравнения неразрывности с учетом условия v2 = 0 при x2 = 0 следует, что
x2
Z
v2 = − ∂v1 dx2 = O(v∞δ0/L), (65) ∂x1
0
т. е. v2/v∞ = O(δ0/L). Таким образом, оба слагаемых в левой части (64) имеют одинаковый порядок O(v∞W0/L), а в правой части первое слагаемое имеет порядок O(νDW0/L2), существенно меньший, чем порядок O(νDW0/δ02) второго слагаемого. Поэтому первым слагаемым можно пренебречь по сравнению со вторым. В итоге, сопоставляя порядки O(v∞W0/L) и O(νDW0/δ02) величин слагаемых, сохраняемых в (64), получаем
L |
= O r |
|
= O √ReL , |
(66) |
|
v∞L |
|||||
δ0 |
|
νD |
1 |
|
|
где ReL = v∞L/νD — число Рейнольдса, включающее в качестве характерного размера протяженность L обтекаемой стенки в направлении оси Ox1. Из (66) следует, что относительная толщина пограничного слоя должна уменьшаться с увеличением ReL.
Если в (64), опустив первое слагаемое в правой части и использовав (51), перейти к функции тока ψ3(x1,x2), то получим уравнение
∂ψ3 ∂2ψ3 |
− |
∂ψ3 ∂2ψ3 |
= νD |
∂ψ3 |
(67) |
||||
|
|
|
|
|
|
|
|||
∂x2 ∂x1∂x2 |
∂x1 ∂x22 |
∂x22 |
|||||||
с граничными условиями: ψ3 = 0 и ∂ψ3/∂x2 = 0 при x2 = 0, x1 > 0; ∂ψ3/∂x2 → v∞ при x2 →
∞, x1 > 0 и ∂ψ3/∂x2 = v∞ при x1 = 0, x2 > 0. В постановку этой задачи входят величины, размерности которых можно выразить лишь через две независимые единицы измерения: метр (м) и секунда (с), что позволяет перейти от уравнения в частных производных к обыкновенному дифференциальному уравнению (ОДУ) с безразмерной искомой функцией f(η) = ψ3/√νDv∞x1, зависящей от одного безразмерного аргумента η = x2pv∞/(νDx1), который включает оба независимых переменных x1 и x2. В таком случае говорят, что задача имеет автомодельное («самоподобное») решение.
Представляя (67) и граничные условия через введенные безразмерные величины, получаем ОДУ
2f000(η) + f(η)f00(η) = 0 |
(68) |
с граничными условиями f(0) = f0(0) = 0 и f0(∞) = 1, причем условие при x = 0 удовлетворяется автоматически. Проведенное с высокой точностью численное интегрирование ОДУ

35
позволило получить зависимость f(η), по которой можно скорости
v = v1/v∞ = f0(η), представленный сплошной линией на рис. 0.11. С погрешностью до 1% изменение v1/v∞
завершается при η ≈ 5, т. е. в качестве толщины по-
p
граничного слоя можно принять δ ≈ 5 νDx1/v∞. По мере увеличения x1 растет и толщина пограничного слоя, но безразмерный профиль скорости остается неизменным (подобным самому себе). Штриховой линией на рис. 0.11 показана вычисленная при помощи (51)
зависимость v2 = v2 √Rex = 1 ηf0(η) − f(η) , где Rex = v∞x1/νD Рис— число. 0.11Рейнольдса, v∞ 2
вычисленное по текущему значению координаты x1. Таким образом, по мере удаления от поверхности стенки v2 возрастает, т. е. жидкость при обтекании стенки оттесняется от ее поверхности вследствие увеличения толщины пограничного слоя вдоль по течению.
Зависимости
∞ |
|
|
|
|
|
|
|
|
|
||
δ = Z0 |
1 − v∞ |
dx2 |
≈ 1,73r |
|
, |
|
|||||
v∞ |
|
||||||||||
|
|
|
|
v1 |
|
|
|
|
νDx1 |
|
|
∞ |
1 − v∞ dx2 |
≈ 0,664r |
|
||||||||
δ = Z0 |
|
v∞ |
v∞ |
||||||||
|
|
v1 |
|
|
|
v1 |
|
|
|
|
νDx1 |
от x1 называют соответственно толщиной вытеснения и толщиной потери импуль-
са. Величина v∞δ равна уменьшению объемного расхода вязкой жидкости, проходящей через пограничный слой, по сравнению с расходом идеальной жидкости, а толщина δ характеризует потерю вязкой жидкостью количества движения вследствие трения.
Напряжение трения на поверхности обтекаемой плоской стенки τ0 = µD∂v1/∂x2 x2=0 ≈
p |
|
|
|
|
|
|
|
|
и ρ — динамическая вязкость и |
|
||||
µDρv∞3 /x1 = 0,664(ρv∞2 |
|
|
∞ |
|
≈ |
|
плот- |
|||||||
0,332 |
/2)/√Rex,2 |
где |
µD |
|||||||||||
ность жидкости. Величину Cf = τ0/(ρv |
|
/2) |
|
0,664/ |
|
= δ /x1 называют |
|
|
||||||
|
|
Rex |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
√ |
местным |
|||
коэффициентом трения.
Используем введенные выше масштабы величин для оценки слагаемых в уравнениях Навье — Стокса (11), которые в случае установившегося обтекания плоской стенки при
отсутствии объемных сил принимают вид |
|
|
|
|
|
|
|
|
|
|||||||
v1 |
∂v1 |
+ v2 |
∂v1 |
+ |
1 ∂p |
= νD |
∂2v1 |
+ νD |
∂2v1 |
, |
|
|
||||
|
|
|
|
|
|
|
|
|||||||||
∂x1 |
∂x2 |
ρ ∂x1 |
∂x1 |
∂x2 |
|
|||||||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
||||||
|
∂v2 |
|
∂v2 |
|
1 ∂p |
|
2 |
v2 |
|
2 |
v2 |
|
(69) |
|||
|
|
|
|
∂ |
|
∂ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v1 |
|
+ v2 |
|
+ |
|
|
|
= νD |
|
|
+ νD |
|
|
, |
|
|
∂x1 |
∂x2 |
ρ ∂x2 |
∂x12 |
∂x22 |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где p — давление. С учетом (65) и (66) по аналогии с (64) слагаемые в левых частях
уравнений (69) |
|
v∞2 δ0 |
|
|
v∞2 |
|
|
|
|
, |
|
|
|
|
|
|
— O L , |
|
||||||||||||
|
|
|
|
|
имеют одинаковый порядок |
|
причем в первом уравнении |
|
|
|
v∞2 |
|
а |
|||||||||||||||||
во втором — O |
|
|
|
= O |
L√ |
|
|
. Также по аналогии с (64) вторым слагаемым |
||||||||||||||||||||||
|
L2 |
|||||||||||||||||||||||||||||
|
ReL |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
уравнений можно пренебречь по сравнению с третьим |
|
которое в |
|||||||||||||||||||||
в правых частях этих |
|
|
|
|
|
|
|
2 |
|
|
, |
Lδ0 |
|
|
||||||||||||||||
|
v∞2 |
|
|
|
|
|
|
|
|
|
|
δ02 |
|
L |
|
|
||||||||||||||
первом уравнении имеет порядок O |
νDv∞ |
|
|
= O |
v∞ |
, а во втором — O |
νDv∞δ0 |
|
= |
|||||||||||||||||||||
|
√ |
|
, |
|
|
|
|
|
|
(69) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= O |
|
|
. |
При продольном обтекании плоской стенки можно принять ∂p/∂x1 = 0. |
||||||||||||||||||||||||||
L |
ReL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом |
|
первое уравнение |
|
|
|
|
можно записать в виде |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂v1 |
|
|
∂v1 |
∂2v1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
v1 |
|
|
+ v2 |
|
= νD |
|
, |
|
|
|
|
(70) |
|||||||||
|
|
|
|
|
|
|
|
|
∂x1 |
∂x2 |
∂x22 |
|
|
|
|
|||||||||||||||
а из второго при ReL 1 следует, что ∂p/∂x2 ≈ 0, поскольку в нем все слагаемые имеют порядок, малый по сравнению с порядком слагаемых первого уравнения.

36
Оценивая аналогичным путем порядок слагаемых в (56) и (57), получим, что тепломассоперенос в пограничном слое при установившемся обтекании плоской стенки несжимаемой жидкостью описываются уравнениями
|
∂T |
|
∂T |
νD ∂2T |
|
∂C |
|
∂C νD ∂2C |
|
|||||||||||
v1 |
|
|
+ v2 |
|
= |
|
|
|
|
, |
v1 |
|
+ v2 |
|
= |
|
|
|
, |
(71) |
∂x1 |
∂x2 |
Pr ∂x |
2 |
∂x1 |
|
|
2 |
|||||||||||||
|
|
|
2 |
|
|
|
∂x2 |
Sc ∂x |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
где T и C — температура жидкости и объемная концентрация некоторого вещества в |
||||||||||||||||||||
жидкости; Pr = νD/a(T ) |
и Sc = νD/D(C) |
— числа Прандтля и Шмидта; a(T ) — темпе- |
||||||||||||||||||
ратуропроводность жидкости; D(C) — коэффициент концентрационной диффузии этого |
||||||||||||||||||||
вещества. При этом для масштабов δ(T ) |
и δ(C), оценивающих порядок толщины тепло- |
|||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
вого и концентрационного пограничных слоев, с учетом (66) получим соответственно
δ0(T )/δ0 = O(1/√Pr) и δ0(C)/δ0 = O(1/√Sc).
Если в (70) и (71) перейти к безразмерным переменным
v = v1 , θ = T − Tп , C = C − Cп , |
||
v∞ |
T∞ − Tп |
C∞ − Cп |
где Tп, T∞ = const — температуры поверхности стенки и жидкости за пределами пограничного слоя; Cп = const, C∞ = const — объемная концентрация вещества около стенки и за пределами пограничного слоя, то при Pr = Sc = 1 эти уравнения станут с точностью до обозначений тождественными, а толщины всех пограничных слоев одинаковыми. Это означает совпадение безразмерных профилей скорости, температуры и объемной концентрации по толщине пограничного слоя, т. е. v = θ = C, характеризующее так называемую тройную аналогию между переносом количества движения, теплоты и вещества. Поскольку на поверхности стенки при x2 = 0 в соответствии с законами Био — Фурье и Фика соответ-
ственно плотность теплового потока
q0 |
= λ(T ) ∂x2 x2=0 |
= λ(T )(T∞ − Tп) ∂x |
|
|
|||
2 x2=0 |
|||||||
|
|
∂T |
|
|
∂θ |
|
|
|
|
|
|
|
|
|
|
и плотность потока вещества
|
|
j0 |
|
= D(C) |
∂x2 x2 |
|
|
|
|
|
x2=0, |
||
|
|
|
=0 = D(C)(C∞ − Cп) ∂x2 |
||||||||||
|
|
(C) |
|
∂C |
|
|
|
|
|
∂C |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
передаваемые от жидкости к стенке, из тройной аналогии следует |
|||||||||||||
Cf |
= St = |
|
q0 |
|
|
= |
α |
= StC = |
|
|
j0(C) |
||
|
2 |
ρcvv∞(T∞−Tп) |
|
v∞(C∞−Cп) |
|||||||||
|
ρcvv∞ |
|
|||||||||||
= |
αC |
, |
(72) |
v∞ |
|
||
где St и StC — число Стантона (тепловое) и число Стантона концентрационное;
α и αC — коэффициенты теплообмена и массообмена; cv — теплоемкость жидкости
при постоянном объеме. Тройную аналогию широко используют при построении ММ тепломассопереноса.
После подстановки в первое уравнение (71) выражений для v1 и v2 и перехода к без-
размерной температуре θ получим ОДУ θ00(η) + Prf(η)θ0(η)/2 = 0 с граничными условиями θ(0) = 0 и θ(∞) = 1, интегрирование которого дает
θ(η) = |
η |
2 |
|
ξ |
f(ξ0)dξ0 |
dξ . |
|||
Z0 exp − |
|
Z0 |
|||||||
|
|
|
Pr |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
η |
|
|
||
|
|
Z exp − |
2 |
Z |
f(ξ)dξ dη |
||||
|
|
|
|
Pr |
|
|
|
|
|
00

37
В силу (68)
ηη
Z |
f(ξ)dξ = −2Z |
f000(ξ) |
dξ = −2ln |
f00 |
(η) |
||
|
|
|
|
, |
|||
f00(ξ) |
f00 |
(0) |
|||||
00
exp − 2 |
η |
f(ξ)dξ = |
f00 |
(0) |
|
|
, |
||||||||
Z0 |
|
||||||||||||||
|
|
Pr |
|
|
|
|
|
|
|
f00 |
(η) |
|
Pr |
||
в итоге получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
η |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
f |
00(ξ) |
Pr dξ |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
|
θ(η) = |
|
|
. |
|
|
|
||||||||
|
|
∞ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Z |
f |
00(η) |
Pr dη |
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Отсюда при Pr = 1 следует уже установленное совпадение безразмерных профилей температуры и скорости.
Использовав (72) и аппроксимацию dθ(0)/dη = 0,332Pr1/3 (0,5 6 Pr 6 50), запишем
q0 |
= α(T∞ − Tп) = λ |
|
∂x2 |
x2=0 |
= λ |
|
(T∞ − Tп)θ |
(0)r |
|
= |
||
|
|
νDx |
||||||||||
|
|
(T ) |
∂T |
|
|
(T ) |
|
|
0 |
|
v∞ |
|
= 0,332Pr1/3 Re1x/2λ(T ) T∞ − Tп ,
x1
или Nux = 0,332Pr1/3Re1x/2, где Nux = αx1/λ(T ) — число Нуссельта, вычисленное по текущему значению x1. Для плоской стенки длиной L в направлении обтекания интегрированием по x1 получим NuL = αL/λ(T ) = 0,664Pr1/3Re1L/2, где α — значение коэффициента теплообмена, усредненное по поверхности стенки. Преобразованием второго уравнения (71) можно получить аналогичный результат и для коэффициента массообмена.
При обтекании криволинейной поверхности изменение давления в направлении обтекания может стать существенным. Но за пределами пограничного слоя вязкость движущейся жидкости проявляется слабо. Поэтому можно воспользоваться интегралом Бернулли (23) и, полагая при малой толщине пограничного слоя по сравнению с радиусами кривизны обтека-
1 |
|
∂p |
|
dv(x1) |
|
|
емой поверхности течение по-прежнему плоским, при B ≡ 0 принять |
|
|
|
= −v(x1) |
|
, |
ρ |
|
∂x1 |
dx1 |
|||
где x1 — координата, отсчитываемая по поверхности в направлении обтекания, а v — скорость жидкости на внешней границе пограничного слоя, которая может быть найдена при помощи ММ безвихревого обтекания поверхности идеальной несжимаемой жидкостью.
лучаем, |
|
|
|
(69) |
|
|
|
|
|
|
|
|
, |
|
|
v2dx1 |
= O L |
, |
|
(70) |
|
- |
||
Тогда |
подставляя это равенство в |
|
и учитывая |
|
что |
|
dv |
v∞2 |
|
вместо |
|
по |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
∂v1 |
|
∂v1 |
|
|
dv |
|
|
|
|
|
∂ v1 |
|
|
|
|
|
|
|||||
|
v1 |
|
|
+ v2 |
|
|
= v |
|
|
|
|
+ νD |
|
. |
|
|
|
(73) |
||||||
|
∂x1 |
∂x2 |
dx1 |
|
|
∂x22 |
|
|
|
|||||||||||||||
Использовав уравнение неразрывности |
|
∂v1 |
+ |
|
∂v2 |
= 0 для установившегося плоского |
||||||||||||||||||
|
|
|
∂x2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
∂x1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
течения и (73), запишем
|
|
|
|
|
|
|
|
|
|
||||||||
|
v1 |
dv |
+ v |
|
∂v1 |
+ |
∂v2 |
|
= |
∂(v1v) |
+ |
∂(v2v) |
|||||
v1 ∂x1 + v2 |
dx1 |
+ v1 |
|
∂x1 |
|
∂x2 |
|
|
∂x1 |
|
∂x2 |
||||||
∂x2 |
∂x1 |
+ ∂x2 |
= ∂x1 + |
|
∂x2 |
||||||||||||
|
∂v1 |
∂v1 |
|
|
|
∂v1 |
|
|
∂v2 |
|
|
∂v12 |
∂(v1v2) |
||||
dv = v1 dx1 ,
dv ∂2v1 = v dx1 + νD ∂x22 .

38
Вычитая почленно из первого равенства второе, получаем
∂x1 |
+ |
∂x2 |
+ (v − v1) dx1 = −νD |
∂x22 . |
|||
∂ v1(v − v1) |
|
|
∂ v2(v − v1) |
|
|
dv |
∂2v1 |
После интегрирования по x2 в пределах от 0 до ∞ с учетом изменения порядка интегрирования по x2 и дифференцирования по x1 запишем
d(v2δ ) |
+ vδ |
dv |
= |
τ |
= |
Cf |
. |
dx1 |
|
dx1 |
ρv2 |
2 |
|
||
Это интегральное соотношение позволяет, задаваясь приближенным профилем скорости v1 в пределах пограничного слоя, найти связь между местным коэффициентом трения на обтекаемой поверхности и изменением скорости v на внешней границе пограничного слоя. Аналогичные интегральные соотношения можно получить для теплового и концентрационного пограничных слоев.
