
МММСС (От Кувыркина Г.Н.) / 88
.pdf
21
|
|
|
|
|
|
|
|
|
vb = v3 |
(0) |
r0 |
|
4µDl |
|
πr04 |
p |
||||||||||||
симальная скорость |
|
|
|
= |
r02 |
p |
, а объемный расход жидкости |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Qж = 2π Z0 |
v3(r)r dr = |
|
, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
8µDl |
|||||||||||||||||||
|
= |
Qж |
= |
r02 p |
= |
v |
|
и Rг = |
|
p |
= |
8µDl |
. Используя соотношение |
|||||||||||||||
v |
||||||||||||||||||||||||||||
2 |
8µDl |
b |
|
4 |
||||||||||||||||||||||||
|
|
πr0 |
|
|
|
|
Qж |
|
|
|
πr |
0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
λгl |
|
|
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p = |
|
ρv |
, |
|
(44) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 |
|
|
|
|
|||||||
где d = 2r0, кроме гидравлического сопротивления Rг канала вводят коэффициент λг сопротивления движению жидкости. Из полученных результатов следует, что для круглой трубы
λг = |
2d p |
= |
64 |
, |
(45) |
||
|
|
2 |
Re |
||||
lρv |
|||||||
где Re = vd/νD — число Рейнольдса, характеризующее соотношение между силами инерции и силами вязкости при течении жидкости. Значение Re используют в качестве критерия, устанавливающего границу сохранения ламинарного течения в канале. Для круглой трубы принимают, что течение сохраняется при условии Re 6 2300, хотя при снижении возмущений на входе в трубу с достаточно гладкой поверхностью стенки удавалось сохранить ламинарный режим течения при Re 6 50000. При более высоких значениях Re происходит потеря устойчивости ламинарного режима и течение переходит в турбулентное, при котором частицы жидкости совершают неустановившиеся беспорядочные движения по сложным траекториям.
Точное решение в аналитической форме удается получить для течения вязкой жидкости в цилиндрических каналах с поперечным сечением в виде кругового кольца, прямоугольника, равностороннего треугольника и эллипса. Для оценки сопротивления цилиндрических каналов с произвольным поперечным сечением площадью F используют (44) и (45), но в (44) и в выражение для Re вместо диаметра d = 2r0 круглого поперечного сечения подставляют так называемый гидравлический диаметр dг = 4F/Πж, где Πж — «смоченная» жидкостью часть периметра контура поперечного сечения канала. Ясно, что для трубы с круглым поперечным сечением dг = d. Однако такая оценка значения λг может оказаться слишком грубой. Например, для рассмотренной выше плоской щели dг = 4h и, согласно (44) и (45),
|
|
|
|
|
|
2 |
|
2µDlv |
|
µDlQж |
|
|||
p = 64νD |
l ρv |
= |
= |
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
dг 2vdг |
|
h2 |
|
h3 |
||||||||||
|
|
|
|
|
|
|||||||||

22
т. е. p/Qж = µDl/h3, что в 1,5 раза меньше значения Rг, которое следует из точного решения. Этот пример показывает, что гидравлическое сопротивление канала при ламинарном течении надежнее находить путем непосредственного анализа исходной ММ.
Двустороннюю оценку гидравлического сопротивления канала произвольного поперечного сечения площадью F с полностью смоченным контуром можно получить при помощи двойственной вариационной формы ММ, включающей альтернативные функционалы
J[v3] = Z |
v |
)2 |
|
p |
|
dF, I[f] = −Z |
f 2 |
|
(r2 3 |
|
− |
v3 |
| | |
dF, (46) |
|||
2 |
|
µDl |
2µD |
|||||
F |
|
|
|
|
|
F |
|
|
где r2 = (∂/∂xi)ei — дифференциальный оператор Гамильтона, дей-
ствующий в плоскости x1Ox2 поперечного сечения канала. Первый из этих функционалов допустимо рассматривать на функциях v3(M), M F , имеющих кусочно непрерывные производные и удовлетворяющих условию v3(P ) = 0, P , а второй — на векторных функциях f(M), M F , удовлетворяющих уравнению r2 ·f = p/l. Уравнением Эйлера — Лагранжа по отношению к J[v3] является обобщение урав-
нения (41): |
|
|
|
r22v3 = − |
p |
, |
(47) |
|
|||
µDl |
где r22 — дифференциальный оператор Лапласа, определенный в плос-
кости x1Ox2.
Функция v3, удовлетворяющая (47), на допустимом множестве функций v3 минимизирует функционал J[v3], а функция f = −µDr2v3 на допустимом множестве функций f максимизирует функционал I[f], при этом выполняются неравенства J[v3] > J[v3] = I[f ] > I[f]. Исполь-
зуя теорему Остроградского — Гаусса и учитывая (47), находим
J[v3] = Z |
|
r22 3 |
)2 |
− µDpl v3 |
dF = 2 Z |
v3(r2v3)nd − |
|||||
|
( |
v |
|
|
|
1 |
|
||||
F |
|
|
|
|
|
|
|
|
|
|
|
Z
− 12
F
|
p |
|
p |
(Δp)2 |
|||
v3r22v3 dF − |
|
Z |
v3 dS = − |
|
Qж = − |
|
, |
µDl |
2µDl |
2µDlRг |
|||||
|
|
F |
|
|
|
|
|
где n — единичный вектор внешней нормали к контуру . В итоге получаем двустороннюю оценку для Rг в виде
|
(Δp)2 |
(Δp)2 |
|
||
− |
|
6 Rг 6 − |
|
. |
(48) |
2µDlJ[v3] |
2µDlI[f] |
||||
23
Например, в случае течения в канале с квадратным поперечным сечением площадью F = 4a2 при выборе начала координат в центре квадрата допустимой для J[v3] будет функция v3(x1,x2) = = C(a2 − x21)(a2 − x22), C = const. Подставляя эту функцию в первое равенство (47), получаем
|
C2 |
a a |
|
J[v3] = |
Z Z 4x12(a2 − x22)2 + 4x22(a2 − x12)2 dx1 dx2 − |
||
2 |
−a −a
a a
p Z Z
− C µDl
−a −a
(a2 − x12)(a2 − x22) dx1 dx2 = |
128 |
|
16 |
|
p |
|
|
C2a8 − |
|
C |
|
a6. |
|
45 |
9 |
µDl |
||||
Из необходимого условия |
|
∂J[v3] |
= 0 минимума функционала найдем кон- |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
5 |
|
|
p |
|
|
|
|
|
|
|
∂C |
|
|
|
|
|
|
|
5 |
|
|
|
a2 |
p |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
станту C = |
|
|
|
, |
а затем вычислим значение J[v3] = − |
|
|
|
|
. |
|||||||||||||||||||||
16 |
a2µDl |
18 |
|
µDl |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
В качестве функции |
допустимой для I[f], примем f = |
|
p |
|
|
|
|
x1 + x2 . |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Подставляя ее во второе, |
равенство (47), находим |
|
|
|
l |
r2 |
|
4 |
|
|
|
||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
a |
a |
1 |
|
a2 |
|
|
|
|
|
|
|
|
|
|
||||
I[f] = − |
|
|
|
p |
|
2 |
Z Z 4(x12 + x22)dx1 dx2 = − |
|
p |
|
|
|
2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||||
2η2 |
|
4l |
|
|
|
3 |
|
µDl |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
− |
a |
− |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, учитывая (48), имеем 1,5µDl/a4 6 Rг 6 1,8µDl/a4. Из точного решения следует Rг ≈ 1,775µDl/a4, что достаточно близко к полученной верхней оценке. Для рассматриваемого канала dг = 2a, поэтому, согласно (45) и (45), получим Rг = p/Qж = 2µDl/a4, т. е. примерно на 11 % выше полученной верхней оценки и почти на 13 % выше значения Rг, которое следует из точного решения.
При прямолинейном движении вязкой жидкости в канале в некоторых случаях удается получить точное решение и для более сложных по сравнению с (7) реологических уравнений, описывающих свойства так называемых неньютоновских жидкостей. В частности, эти уравнения применяют для описания свойств широкого класса сред, используемых в технике и технологических процессах: расплавленных металлов, полимеров, нефтепродуктов, бетонов, силикатов, грунтов и т. п. В качестве примера рассмотрим уравнение
−V23 = |
τ |
+ knτn, kn, n = const, |
(49) |
2µD |
связывающее компоненту V23 тензора скоростей с возникающим при этом касательным напряжением τ.

24
Учитывая условие равновесия 2lτ = 2x2 p слоя жидкости толщиной 2x2 и длиной l при ее установившемся движении в плоской щели (см. рис. 0.7) с неподвижными стенками, а также (49) и равенство
V23 = 1 dv3(x2) , получаем ОДУ
2dx2
|
dv3(x2) |
|
px2 |
+ 2kn |
px |
|
n |
|
− |
|
|
= |
|
2 |
|
||
dx2 |
µDl |
µDl |
|
|||||
с граничным условием v3(h) = 0. После интегрирования находим
v (x ) = |
p(h2 − x22) |
+ 2k |
n |
p |
|
n |
hn+1 − x2n+1 |
. |
2µDl |
µDl |
|
||||||
3 2 |
|
|
n + 1 |
|||||
При установившемся течении в трубе с круглым поперечным сечением радиусом r0 условием равновесия объема жидкости в виде цилиндра длиной l и радиусом r 6 r0 будет 2πrlτ = πr2 p. Отсюда, заменив в (49) V23 на (1/2)dv3(r)/dr, получим ОДУ
|
|
|
− |
dv3(r) |
= |
|
pr |
|
+ 2kn |
|
|
pr |
|
n |
|
||||||||
|
|
|
|
dr |
|
|
2µDl |
|
2µDl |
|
|
|
|
||||||||||
с граничным условием v3(r0) = 0 и после интегрирования найдем |
|||||||||||||||||||||||
v |
(r) = |
p(r02 − r2) |
+ 2k |
|
|
p |
|
|
n |
r0n+1 − rn+1 |
. |
||||||||||||
|
|
n 2µDl |
|
|
|
|
|
||||||||||||||||
3 |
|
|
|
|
4µDl |
|
|
|
|
|
|
|
|
n + 1 |
|
||||||||
Объемный расход жидкости через трубу |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
r0 |
|
|
|
|
|
|
πr4 p |
|
|
|
p |
|
|
n n + 1 |
|
|||||||
Q = 2π Z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
v3(r)r dr = 8µDl |
|
+ πkn 2µDl n + 3 r0 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
n+3 |
||
нелинейно зависит |
от |
p. |
Поэтому гидравлическое сопротивление |
||||||||||||||||||||
трубы при течении рассматриваемой жидкости будет зависеть от Qж (или от p).
Если при движении жидкости вектор v ее скорости параллелен некоторой плоскости, например координатной плоскости x1Ox2, и не зависит от координаты x3, то говорят о плоском течении, причем v1 = v1(x1,x2,t), v2 = v2(x1,x2,t), v3 ≡ 0 и в (13) (W · rx)v = 0, так как ненулевой может быть лишь проекция W3 вектора W завихренности.
В этом случае из (13) следует уравнение переноса завихренности |
|
||||
|
∂W3 |
+ vi |
∂W3 |
= νDr22W3, i = 1, 2. |
(50) |
|
∂t |
∂xi |
|||

25
Помимо (50) в ММ, описывающую плоское течение несжимаемой ньютоновской жидкости, входят уравнение неразрывности и выражение
W3 = ∂v2 − ∂v1 . Однако при этом сохраняется проблема корректной
∂x1 ∂x2
формулировки граничных условий для W3 на непроницаемых участках контура , ограничивающего двумерную область F , в которой реализуется плоское течение.
В плоском течении ненулевой является лишь проекция ψ3 векторной
функции тока, причем |
|
|
|
|
|
|
v1 = |
∂ψ3 |
|
v2 = − |
∂ψ3 |
(51) |
|
|
, |
|
. |
|||
∂x2 |
∂x1 |
|||||
Следовательно, уравнение неразрывности в виде ∂vi/∂xi = 0 удовлетворяется тождественно. Значение ψ3 постоянно вдоль каждой линии тока, которая при установившемся движении совпадает с траекторией частиц жидкости, а объемный расход жидкости между двумя любыми линиями тока пропорционален разности значений ψ3, соответствующих этим линиям. Учитывая (51) и выражение для W3, получаем уравнение
r22ψ3 = −W3, |
(52) |
которое в сочетании с (50) в виде
∂W3 |
+ |
∂ψ3 ∂W3 |
− |
∂ψ3 ∂W3 |
= νDr22W3 |
(53) |
||||
|
|
|
|
|
|
|
||||
∂t |
∂x2 ∂x1 |
∂x1 ∂x2 |
||||||||
формирует еще один вариант ММ, описывающей плоское течение. При решении прикладных задач граничные условия для W3 на непроницаемых участках контура обычно получают последовательными приближениями из решения (52).
Если при помощи (52) исключить W3 из (53), то получим
|
∂(r22ψ3) |
+ |
∂ψ3 |
|
∂(r22ψ3) |
|
∂ψ3 |
|
∂(r22ψ3) |
= ν |
4 |
ψ |
, |
(54) |
|||||||
|
|
∂x2 |
|
∂x1 |
− |
∂x1 |
|
Dr2 |
|||||||||||||
|
∂t |
|
|
|
|
|
∂x2 |
3 |
|
|
|||||||||||
|
|
|
|
4 |
|
2 |
2 |
|
4 |
|
|
|
|
|
|
|
|
||||
где r24 = r22(r22) = |
∂ |
+ 2 |
∂ |
|
∂ |
+ |
∂ |
|
|
— дифференциальный бигар- |
|||||||||||
∂x14 |
∂x12 |
∂x22 |
∂x24 |
|
|||||||||||||||||
монический оператор, действующий в плоскости x1Ox2. Несмотря на более высокий порядок производных по пространственным координатам для (54) удается корректно сформулировать граничные условия в любой точке контура .
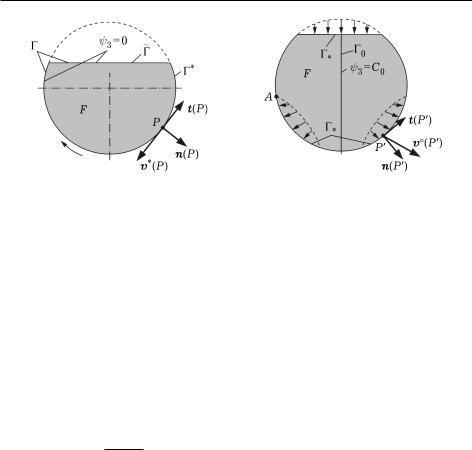
Согласно физическому смыслу функции ψ3 ее значение не изменяется на непроницаемом для жидкости участке контура, т. е. ψ3 = const. Если весь контур , ограничивающий односвязную область F (рис. 0.8),
26
Рис. 0.8 |
Рис. 0.9 |
является непроницаемым, то на нем можно принять ψ3 = 0. На участке (рис. 0.9), через который жидкость вытекает из области F (или поступает в эту область) и на котором задана скорость течения v◦(P ), P , нетрудно вычислить изменение функции тока
s(P )
Z
ψ3(P ) = ψ3(A) + v◦(P 0)n(P 0) ds(P 0), P ,
0
где ψ3(A) — значение функции тока в точке A , от которой отсчитывают длину s(P 0) дуги до текущей точки P 0 с единичным вектором n(P 0) внешней нормали. Это позволяет задать одно граничное условие. Второе граничное условие на этом участке контура следует из (51) и
принимает вид ∂ψ3(P ) = v◦ ·t(P ), где t(P ) — единичный вектор в напра-
∂n(P )
влении касательной к контуру в точке P , повернутый относительно n(P ) против хода часовой стрелки.
Если в области F до решения задачи можно установить линию0 симметрии течения (см. рис. 0.9), то она будет совпадать с одной из линий тока, на которой ψ3 = C0 = const, а в точках P 0 частицы жидкости не будут вращаться, т. е. W3(P ) = 0, и в соответствии с (52) r2ψ3(P ) = 0. Совмещая в любой точке P 0 оси координат с направлениями t(P ) касательной и n(P ) нормали к линии симметрии, в силу инвариантности дифференциального оператора Лапласа относительно поворота прямоугольной системы координат по-
|
|
|
|
∂2ψ3(P ) |
∂2ψ3(P ) |
|
|
||||
лучаем |
|
|
|
|
+ |
|
|
= 0. |
Но так как ψ3(P ) = const, P 0, то |
||
|
∂t2(P ) |
∂n2(P ) |
|||||||||
∂2ψ3(P ) |
= 0 и, следовательно, |
в качестве граничного условия можно |
|||||||||
|
∂t2(P ) |
|
|||||||||
|
|
∂2ψ3(P ) |
|
|
|
|
|
||||
принять |
= 0. |
|
|
|
|||||||
|
∂n2(P ) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
Аналогичные рассуждения можно провести применительно к свободной поверхности жидкости (участок e на рис. 0.8), если пренебречь

27
трением жидкости с воздухом (или иным газом) на этой поверхности. Однако на участке , соответствующем твердой стенке, в силу эффекта прилипания частиц жидкости в точках P вектор v(P ) скорости жидкости равен заданному вектору v (P ) скорости движения стенки.
Поэтому в соответствии с (51) на такой стенке |
|
∂ψ3(P ) |
= v (P ) · t(P ), |
||
|
∂n(P ) |
|
|||
P . Ясно, что в случае неподвижной стенки |
∂ψ3(P ) |
= 0. |
|||
∂n(P ) |
|
||||
Таким образом, в каждой точке контура , ограничивающего двумерную область F , удается задать по два граничных условия для функции ψ3, необходимых для построения ММ, включающей (54). Эти граничные условия можно записать в достаточно общем виде следующим
образом: |
(P ) = ψ3◦ = const, |
∂∂n23(P ) = 0, |
P 1 ; |
|
|
||||
ψ3 |
|
||||||||
|
|
|
|
2 |
ψ (P ) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
∂ψ3(P ) |
|
|
|||||
ψ (P ) = f (P ), |
|
|
|
|
|
|
|
|
|
|
|
|
= f (P ), P = , |
(55) |
|||||
|
|
∂n(P ) |
|
|
|
|
|||
3 |
0 |
1 |
|
2 \ 1 |
|
||||
где 1 — участки контура, соответствующие свободной поверхности жидкости или линии симметрии течения; f0(P ) и f1(P ) — заданные функции точки на участках 2 контура, а число ψ3◦ обычно можно принять равным нулю.
Используя соотношения rvr = −∂ψ/∂z и rvz = ∂ψ/∂r, можно ввести функцию тока ψ(r,z) для осесимметричного относительно оси Oz течения, в котором вектор скорости имеет в цилиндрической системе координат проекции vr и vz на радиальное и осевое направления соответственно. Тогда уравнение неразрывности (3.33) в виде 1r ∂rv∂rr +
∂v∂zz = 0 удовлетворяется тождественно, а вместо (54) можно получить уравнение относительно ψ, содержащее производные этой функции по координатам r и z до четвертого порядка включительно. Граничные условия для ψ формулируются аналогично (55). Функция тока может быть введена и для осесимметричного течения, рассматриваемого в
сферической системе координат.
1.5. Модели тепломассопереноса в несжимаемой жидкости
При движении вязкой жидкости в силу диссипации механической энергии и теплообмена с обтекаемыми твердыми телами в общем случае может возникнуть неоднородное по объему жидкости распределение температуры, описываемое уравнением теплопереноса (8). В случае несжимаемой изотропной жидкости и в отсутствие внутренних источников теплоты оно примет вид
ρcv |
∂t |
+ vi ∂xi |
= 2µDVijVij + |
∂xi λ(T ) |
∂xi , i, j = 1, 2, 3, |
||
|
|
∂T |
|
∂T |
|
∂ |
∂T |

28
где ρ, cv, µD и λ(T ) — плотность, теплоемкость при постоянном объеме, динамическая вязкость и теплопроводность жидкости; T — температура; t — время; vi — проекция
1 |
|
∂vi |
|
∂vj |
— |
|
вектора скорости на ось Oxi прямоугольной системы координат; Vij = |
|
|
+ |
|
||
2 |
∂xj |
∂xi |
||||
компоненты тензора скоростей. В большинстве прикладных задач можно пренебречь диссипацией механической энергии и считать λ(T ) = const, что позволяет представить уравнение теплопереноса в виде
∂T |
∂T |
(T ) |
∂2T |
|
|||
|
+ vi |
|
= a |
|
. |
(56) |
|
|
|
|
|
||||
∂t |
∂xi |
|
∂xi∂xi |
|
|||
где a(T ) = λ(T )/(ρcv) — температуропроводность жидкости.
Помимо (56) в математическую модель (ММ), описывающую процесс теплопереноса,
войдут уравнение неразрывности ∂vi и уравнения Навье — Стокса (12), а в случае плос-
∂xi
кого течения — либо (50) – (52), либо (51) и (54) с соответствующими краевыми условиями.
Если в жидкости присутствует некоторое вещество, массу которого в единице объема опре-
деляет объемная концентрация C, и происходят явления концентрационной диффузии, термодиффузии и бародиффузии, то ММ следует дополнить уравнением переноса этого вещества
∂t |
+ vi ∂xi |
= ∂xi |
D(C) ∂xi |
+ T |
D(T ) ∂xi |
+ p D(p) |
∂xi , |
|||||
∂С |
|
∂С |
|
∂ |
|
∂C |
C |
|
∂T |
|
C |
∂p |
где D(C), D(T ) и D(p) — коэффициенты концентрационной диффузии, термодиффузии
и бародиффузии этого вещества; p — давление. Часто можно ограничиться учетом лишь явления концентрационной диффузии при условии D(C) = const, что приводит последнее уравнение к виду
∂С |
∂С |
(C) |
∂2C |
|
|||
|
+ vi |
|
= D |
|
. |
(57) |
|
|
|
|
|
||||
∂t |
∂xi |
|
∂xi∂xi |
|
|||
Вэтом случае ММ описывает процесс тепломассопереноса в несжимаемой жидкости
впредположении C ρ, что позволяет не учитывать влияние C на значения ρ, µD и a(T ). Если движение жидкости вызвано внешними механическими воздействиями (например, перепадом давления, создаваемым насосом или возникающим при обтекании твердого тела), то говорят, что тепломассоперенос определяется вынужденной конвекцией. Плотность ρ несжимаемой жидкости в некоторой степени зависит от T и C. Поэтому при их неоднородном распределении в объеме жидкости возникает и неоднородное распределение ρ, что
вполе силы тяжести или при наличии ускорения приводит к возникновению объемных сил и вызывает движение жидкости, называемое естественной конвекцией. Если объем можно считать неограниченным (например, в случае тепломассопереноса в атмосфере или водоемах), то обычно говорят о свободной конвекции. При сопоставимом влиянии как вынужденной, так и естественной (свободной) конвекции тепломассоперенос определяется
смешанной конвекцией.
Изменение плотности жидкости при сравнительно малом изменении T и C можно представить в виде
ρ 1 + αV(T )(T − T0) = ρ0 + С, |
(58) |
(T )
где αV — температурный коэффициент объемного расширения жидкости; ρ0 — плот-
ность при температуре T0 и C = 0. В неподвижной относительно выбранной системы координат жидкости, имеющей плотность ρ0, согласно (12), ∂p◦/∂xi = b◦i = wiρ0, где p◦ —
гидростатическое давление, b◦i и wi — проекции на оси Oxi векторов b плотности объ-
емных сил и w абсолютного ускорения (например, если на поверхности Земли ось Ox3 неподвижной системы координат направлена вверх, то w3 = −g0, где g0 ≈ 9,81 м/с2 — ускорение свободного падения). Тогда при неоднородных в объеме жидкости распределениях T и C можно принять в левой части (12) ρ = const, а в правой части с учетом (58) и равенства bi = wiρ произвести замену
− |
∂p |
+ b = |
− |
∂(p − p◦) |
+ b |
i − |
b◦ |
= |
− |
∂(p − p◦) |
+ w |
(ρ |
− |
ρ |
) = |
∂xi |
i |
∂xi |
i |
|
∂xi |
i |
|
0 |
|
||||||

29
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
− |
∂(p − p◦) |
− |
w |
i |
ρα(T ) |
(T |
− |
T |
) |
− |
C , |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xi |
|
|
|
V |
|
0 |
|
|
||||||
где p — давление жидкости. В итоге (12) примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
∂vi |
|
|
∂vi |
|
|
1 |
∂(p − p0) |
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
+ v |
|
|
= |
− |
|
|
− |
w |
|
α(T ) |
(T |
− |
T |
) |
− |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
j ∂xj |
ρ ∂xi |
|
i |
V |
|
0 |
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ νD |
∂2vi |
|
, |
i, j = 1, 2, 3, |
(59) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xj∂xj |
|
|
|
|
|
|
|
||||
где νD — кинематическая вязкость.
Наряду с (56), (57) и (59) в ММ, описывающую процесс тепломассопереноса, должны входить так называемые условия однозначности. Они состоят из геометрических, физи-
ческих и краевых условий.
В уравнениях (56), (57) и (59), входящих в ММ теплопереноса, перейдем к безразмерным переменным, выбрав в качестве масштабов длины, скорости, давления, температуры и объемной концентрации L, v0, p0, T0 и C0 соответственно (выбор масштабов целесообразно согласовывать с набором параметров, которые входят в условия однозначности). Тогда получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∂θ |
|
|
|
|
|
|
|
∂θ |
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
+ Pe |
v |
i |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂Fo |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
∂x |
∂x |
i∂x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
∂C |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂C |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|||||||||||||||||
Lu |
|
|
|
|
|
|
+ ReSc |
v |
i |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||||||||||||||
∂Fo |
|
|
i |
|
|
|
|
|
|
|
i |
|
|
||||||||||||||||||||||||||||||||||||||
∂x |
∂x |
i∂x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
i |
+ |
|
|
|
|
|
|
|
i |
= |
|
|
|
Eu |
∂ |
|
|
|
|
wi |
Ra |
θ−1 |
+ |
wi |
|
||||||||||||||||||||||
|
∂v |
|
∂v |
|
|
|
p |
|
|||||||||||||||||||||||||||||||||||||||||||
|
v |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
j |
|
|
|
− |
|
|
i − |w| |
|
|
|||||||||||||||||||||||||||||||||||||
|
∂Ho |
j |
|
|
|
|
|
|
|
|
|
Re2Pr |
|w| |
||||||||||||||||||||||||||||||||||||||
|
∂x |
|
|
|
|
|
∂x |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(60) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 1 ∂2 |
|
i |
, |
|
|
RaСC |
|
||||||
v |
|
||||||
2 |
Sc |
Re ∂xj∂xj |
|
|
|||
Re |
|
|
|||||
где |
|
|
|
T |
|
|
|
|
|
vi |
|
|
|
|
xi |
, |
|
= |
C |
; |
|
|
= |
p − p◦ |
; Fo = |
a(T )t |
— число Фурье; Pe = |
v0L |
— |
||||||||
θ |
= |
|
; |
|
i = |
; |
|
|
i = |
C |
|||||||||||||||||||||||||||
|
v |
x |
p |
||||||||||||||||||||||||||||||||||
T0 |
|
L |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
v0 |
|
|
|
|
|
|
C0 |
|
|
|
p0 |
|
L2 |
|
|
|
|
a(T ) |
|||||||||||
число Пекле; Lu = |
|
a(T ) |
|
— число Лыкова — Льюиса; Re = |
v0L |
— число Рейнольдса; |
|||||||||||||||||||||||||||||||
|
D(C) |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νD |
|||||||||
Sc = |
νD |
|
— число Шмидта; Ho = |
v0t |
— число гомохронности; Eu = |
p0 |
— число |
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
D(C) |
|
|
|
|w|L3αV(T )T0 |
|
|
|
|
|
L |
|
|
|
|
|
ρv02 |
||||||||||||||||||
Эйлера; Ra = |
— число Рэлея; Pr = |
νD |
|
— число Прандтля; RaС = |
|||||||||||||||||||||||||||||||||
|
a(T ) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
νDa(T ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |w|L3C0 — концентрационное число Рэлея.
ρνDD(C)
Не все безразмерные комплексы в (60), являющиеся критериями подобия процессов тепломассопереноса, независимы (например, Ho = FoRePr и Pe = RePr). Совокупность комплексов, состоящих из параметров, входящих в условия однозначности, называют определяющими критериями подобия. Эти критерии могут быть вычислены по исходным данным до количественного анализа ММ процесса или его экспериментального исследования. При геометрическом подобии областей протекания двух процессов, имеющих одинаковую физическую природу, подобии их условий однозначности и попарном равенстве значений одноименных определяющих критериев говорят, что эти процессы подобны, т. е. для таких процессов в моменты времени t, соответствующие равенству значений Fo и Ho, совпадают зависимости безразмерных распределений θ, C, p и vi от безразмерных координат xi.
Для установления совокупности независимых определяющих критериев подобия удобно использовать основные положения теории размерностей, которая на основе анализа связей между размерными параметрами, характеризующими рассматриваемый процесс, позволяет определить структуру ММ этого процесса в виде зависимости между безразмерными комбинациями, составленными из таких параметров.
Размерностью величины или параметра называют произведение степеней независимых единиц измерения физических величин, принятых в качестве основных (стандартных). Известно, что в качестве основных в Международной системе единиц СИ (Systˆeme
30
International) приняты следующие единицы измерения: длины — метр (м), массы — килограмм (кг), времени — секунда (с), силы электрического тока — ампер (А), температуры — кельвин (К), силы света — кандела (кд), количества вещества — моль. Дополнительными (безразмерными) единицами являются радиан (рад) для измерения плоского угла и стерадиан (ср) для измерения телесного угла.
Например, размерность модуля w вектора w ускорения записывают в виде [w ] = = [l]ψl(w) [t]ψt(w) = м/с2, где [l] = м и [t] = с — размерности длины и времени соответственно,
(w) (w)
ψl = 1 и ψt = −2 — показатели этих размерностей в выражении для размерности ускорения. Размерность силы P в системе СИ вводят на основе второго закона Ньютона
P = mw, где m — масса. Отсюда [P ] = [m][w ] = [m]ψm(P ) [l]ψl(P ) [t]ψt(P ) = кг · м · с−2 =
= кг · м/с2 = Н (ньютон), где ψm(P ) = 1, ψl(P ) = 1, ψt(P ) = −2 — показатели размерности массы, длины и времени соответственно в выражении для размерности силы. Ясно, что для величины, равной произведению размерных величин, показатели размерности равны алгебраической сумме соответствующих показателей сомножителей. Например, размерность мощности Q следует из выражения
[Q] = [P ][l] = [m]ψm(P ) [l]ψl(P ) [t]ψt(P ) [l]ψl(l) [t]−ψt(t) = [t]
= [m]ψm(P )
[l]ψl(P )+ψl(l) [t]ψt(P )−ψt(t) ,
где ψl(l) = ψt(t) = 1. В итоге получаем [Q] = [m][l]2[t]−3 = кг · м2/с3 = Вт (ватт). Отметим, что для принятой системы основных единиц измерения размерность любой
величины может быть представлена лишь единственным образом. Итак, наиболее важное предположение теории размерностей состоит в том, что размерность любой рассматриваемой величины ζj можно представить в виде так называемого степенного одночлена
k |
|
iY |
|
[ζj ] = [Li ]ψij , |
(61) |
=1 |
|
где [Li ] — размерности k величин, принятые в качестве основных единиц измерения; ψij — некоторые показатели степени.
Наименьшую совокупность размерных и безразмерных величин, необходимых и достаточных для однозначного описания рассматриваемого процесса, в теории размерностей называют определяющими параметрами. К ним относят геометрические и физические характеристики процесса и независимые переменные, включая пространственные координаты и время. Величины, зависящие от определяющих параметров, называют определяемыми параметрами. Определяющие и определяемые параметры образуют совокупность
основных параметров данного процесса.
Пусть рассматриваемый процесс характеризуют n основных параметров ζj > 0, j = 1, n, для каждого из которых справедливо (61). Рассмотрим степенной одночлен
n |
|
|
jY |
zj |
(62) |
Π = ζj , |
||
=1 |
|
|
где zj — некоторые показатели степени, и найдем число n степенных одночленов этого вида при условии, что они являются независимыми (т. е. ни один из них нельзя представить произведением степеней других) и безразмерными. При помощи (61) выразим размерность Π, равную единице, через размерности k величин, принятых в качестве основных единиц измерения:
Y Y |
|
zj |
iY |
X |
|
n |
k |
|
|
k |
n |
[Π] = |
|
[Li ]ψij |
|
= [Li ]βi = 1, |
βi = ψijzj. |
j=1 |
i=1 |
|
|
=1 |
j=1 |
Таким образом, условием равенства единице размерности степенного одночлена Π является выполнение k равенств βi = 0, i = 1, k, или
n
X
ψijzj = 0, i = 1, k. |
(63) |
j=1
