МММСС (От Кувыркина Г.Н.) / 88

1

1. Математические модели жидкости

Сплошная среда, заполняющая некоторую пространственную об-

ласть и рассматриваемая как изолированная термодинамическая система, в соответствии с нулевым законом термодинамики имеет хотя бы одно естественное состояние. Характерным свойством вещества в жидком и газообразном агрегатных состояниях является то, что оно имеет несчетное множество естественных состояний. В качестве постулата считают, что все состояния, для которых плотность ρ неподвижной среды при постоянной температуре совпадает с начальным значением ρ0, являются естественными. Поэтому в качестве одного из аргументов активных переменных принимают якобиан J = ρ0/ρ, опре-

деляющий в окрестности рассматриваемой точки изменение плотности среды при ее течении. В этой главе под жидкостью будем понимать как жидкое, так и газообразное агрегатные состояния вещества. Чтобы различать эти состояния, в гидромеханике собственно жидкости часто называют капельными.

1.1. Жидкость как сплошная среда скоростного типа

Примем в качестве аргументов активных переменных — массовых плотностей свободной энергии A и энтропии h, тензора напряжений

энергии), где u — массовая плотность внутренней энергии, с учетом равенства u = A + T h запишем

2

где ak — материальные координаты, определяющие положение частицы жидкости в начальной конфигурации, а vk — проекции вектора скорости на оси Oxk системы пространственных координат, то

Используя это равенство и вычитая (2) из неравенства Клаузиуса —

откуда в силу того, что скорости dT/dt, dVij/dt и dϑi/dt изменения реактивных переменных произвольны, следуют достаточные условия реализуемости рассматриваемого процесса:

где первые слагаемые в правых частях равенств, отмеченные индексом (·)◦, не зависят от Vkl, т. е. представляют собой значения активных переменных при Vkl = 0, а вторые слагаемые, отмеченные индексом

(·)(D), зависят от Vkl и обращаются в нуль при Vij = 0. Тогда с учетом (4) получим, что A(D) = 0, т. е. A = A◦, а также h(D) = 0, т. е.

h = h◦. Введем диссипативную функцию δD = σij(D)Vij и представим неравенство (4) в виде

Так как первое слагаемое в левой части этого неравенства линейно зависит от Vij, то

3

Поэтому второй закон термодинамики в данном случае принимает

жидкости.

Жидкость, как правило, изотропна, в связи с этим в линейном приближении тензор вязких напряжений имеет компоненты σij(D) =

характеризующее линейную вязкую (или ньютоновскую) жид-

кость. Из (7) следует, что при контакте с твердой поверхностью в силу конечных значений напряжений возникает эффект прилипания частиц линейной вязкой жидкости к этой поверхности, подтверждаемый экспериментально и объясняемый наличием сил молекулярного сцепления. Это означает, что вектор скорости частицы жидкости, находящейся в контакте с твердой поверхностью, совпадает с вектором скорости соответствующей точки этой поверхности.

Если положить A = A(J ,T ) и определить зависимость вектора плотности теплового потока от реактивных переменных, например, в виде закона Био — Фурье, то, учитывая (2), (4) и (7), после несложных преобразований можно получить уравнение теплопереноса в

ции. Отметим, что в механике жидкости и газа используют термины

удельная теплоемкость при постоянном объеме или изохорная теплоемкость, соответствующая изохорному (при постоян-

ном объеме среды) термодинамическому процессу, и обозначение cv.

чаем уравнения Навье — Стокса — Дюгема для вязкой сжимаемой жидкости

4

где bi — проекции вектора b плотности объемных сил на оси Oxi. Полная система уравнений, описывающих течение жидкости, в рассматриваемом варианте математической модели содержит шесть неизвестных: ρ, T , p и три проекции vi вектора v скорости. Для их определения необходимо совместно решить уравнения (8), (9) и уравне-

Согласно (7) среднее нормальное напряжение в жидкости σkk/3 = = −p + 3κDVkk, где κD = λD + 2µD/3 — объемная вязкость. Если принять, что это напряжение в движущейся жидкости определяется (как и в покоящейся) лишь давлением, то приходим к условию Сток-

Если жидкость несжимаемая и однородная (ρ = const, ∂vj/∂xj = = 0), а также µD = const, то из (9) получим

где rx и r2x — дифференциальные операторы Гамильтона и Лапласа, вычисляемые в системе пространственных координат с радиус-век-

тором x. Вместе с уравнением неразрывности эти уравнения образуют замкнутую систему относительно неизвестных функций v(x,t) и p(x,t), однако не удается корректно задать граничные условия для давления на непроницаемых границах области V , в которой рассматривается движение жидкости.

При сравнительно малой скорости течения жидкости и выполнении неравенства |vj∂vi/∂xj| |∂vi/∂t| говорят о ползучем движении жидкости, описываемом уравнениями

которые отличаются от (12) отсутствием инерционных сил, вызванных переносным ускорением частиц жидкости. При bi = 0 и установившемся

5

этого равенства по xi и суммируя по индексу i, с учетом равенства

∂vi = 0 получаем

∂xi

т. е. для такого движения давление является гармонической функцией: r2xp = 0.

Если существует потенциал B0 векторного поля объемных

rx|v| = 2(v · rx)v + 2v × (rx × v) и выражения для полной производ-

|v| /2 + B0/ρ) + (µD/ρ)rxv. Затем вычислим ротор левой и правой частей этого равенства и с учетом равенства rx × (b × c) = (c · rx)b − c(rx · b) − (b · rx)c + b(rx · c) запишем

поскольку rx×v = W — вектор завихренности, rx · (rx×v) = 0 как смешанное произведение векторов с двумя одинаковыми сомножителя-

где νD = µD/ρ — кинематическая вязкость, м2/с.

Исключение давления из системы уравнений снимает и проблему формулировки граничных условий для функции p(x,t) на непроницаемых границах области V , но порождает аналогичную проблему по отношению к функции W (x,t). Равенством v = rx×ψ можно ввести векторную функцию тока ψ, тождественно удовлетворяющую ра-

венству ∂vj = 0. Тогда W = rx×(rx×ψ) = rx(rx · ψ) − r2 ψ. После

∂xj x

подстановки этого равенства в (13) получим единственное уравнение относительно векторной функции ψ(x,t), содержащее ее производные по пространственным координатам до четвертого порядка включительно. Преимущество математической модели, включающей это уравнение, состоит в том, что для функции ψ(x,t) удается корректно сформулировать по два граничных условия в каждой точке поверхности S, ограничивающей область V .

6

1.2. Идеальная жидкость

Гипотетическую жидкость, полностью лишенную свойства вязкости, принято называть идеальной. Для получения уравнений, описывающих ее движение, достаточно в (11) положить µD = 0. В итоге получим уравнения Эйлера

где ρ — плотность жидкости; vi и bi — проекции векторов v скорости и b плотности объемных сил на оси Oxi системы пространственных координат; t — время; p — давление; rx — дифференциальный оператор Гамильтона, вычисляемый в системе пространственных координат с радиус-вектором x. Для неподвижной жидкости из (15) следуют уравнения ∂p/∂xi = bi, или rxp = b, описывающие состояние

гидростатического равновесия.

Если ρ зависит лишь от p, т. е. ρ = ρ(p), то жидкость называют

баротропной и вводят функцию давления

равную работе, совершаемой при движении единицы массы баротропной жидкости при изменении давления от p0 до p. Во многих приложениях векторное поле плотности массовых сил не зависит от времени и обладает потенциалом B(x), поэтому b/ρ = −rxB. При перечисленных допущениях, учитывая rx|v|2 = 2(v · rx)v + 2v × (rx × v) и выражения для полной производной dv/dt, запишем векторную форму (15) в виде

где W = rx×v — вектор завихренности.

Если из массовых сил действует только сила тяжести, то B = = gh, где g — постоянное ускорение свободного падения, а h —

высота, отсчитываемая от некоторого уровня. Величины h, hp = P/g и hv = |v|2/(2g) называют напором соответственно геометрическим,

пьезометрическим и скоростным. Сумма значений этих напоров

7

Поскольку rx ·(rx×v) = rx ·W = 0, согласно теореме Остроградского — Гаусса для области V пространства, ограниченной поверхностью S и лежащей в области определения поля скоростей, имеем

Z

S

где n — единичный вектор внешней нормали к поверхности S. Подынтегральное выражение в (19) называют потоком вихря через элемент dS поверхности, векторные линии поля W — вихревыми линиями, а поверхность, образованную вихревыми линиями, проведенными через точки замкнутого контура, — вихревой трубкой, которую в случае контура, охватывающего бесконечно малую площадку, называют ви-

хревой нитью.

Пусть dS1 и dS2 — площадки соседних нормальных сечений вихревой нити, а вектор завихренности направлен от dS1 к dS2. Так как поток вихря через боковую поверхность вихревой трубки равен нулю, то, применяя (19) к участку вихревой нити, ограниченному рассматриваемыми сечениями, получаем W1 dS1 = W2 dS2, где W1 и W2 — модули вектора W в сечениях dS1 и dS2 соответственно. Таким образом, |W | изменяется вдоль вихревой нити обратно пропорционально площади ее поперечного сечения. Вихревая нить (или трубка) не может оканчиваться внутри жидкости, она или замкнута или оканчивается на поверхности, ограничивающей жидкость. Справедлива теорема Кельвина (Томсона) о том, что при движении идеальной баротропной жидкости в потенциальном поле массовых сил циркуляция вектора скорости по замкнутому контуру остается постоянной во времени. Следовательно, такая жидкость обладает свойством сохранять безвихревое движение, определяемое выполнением условия W = rx×v = 0 в каждой точке области, занятой этой жидкостью. В этом случае векторное поле скоростей обладает потенциалом Φ(x,t):

Отсюда для несжимаемой жидкости получим уравнение Лапласа

т. е. Φ(x,t) является гармонической функцией.

Для безвихревого движения сжимаемой жидкости из (17) и (20)

следует интеграл Лагранжа — Коши

8

где f(t) — одинаковая для всей области движения жидкости функция времени, определяемая обычно или из граничных условий, или по зависимости от t левой части (22) в какой-либо одной точке этой области. Если движение жидкости установившееся, то ∂Φ/∂t = 0, f(t) =

= const и (22) переходит в интеграл Бернулли B + P + |v|2/2 = const,

который в случае несжимаемой жидкости плотностью ρ0 имеет вид

Система уравнений (22), (24) замкнута относительно неизвестных функций P и Φ, поскольку a2 можно также представить как функцию P .

В ряде прикладных задач аэродинамики и акустики течение среды можно рассматривать как возмущенное относительно известного движения или состояния покоя жидкости. Так, при малых возмущениях относительно состояния покоя, в котором ρ = ρ0 = const, систему (22), (24) можно линеаризовать, если в (22) пренебречь слагаемым |rxΦ|2/2

относящимся к дифференциальным уравнениям гиперболического типа. Значение a0 в (25) является скоростью распространения малых возмущений в среде и носит название скорости звука.

При установившихся колебаниях с некоторой частотой ω функцию Φ можно представить произведением зависящей только от времени t периодической функции вида sinωt или cos ωt (или линейной комбинации этих функций) и функции Φ◦(x), зависящей лишь от пространственных координат и описывающей форму волны. Тогда первое уравнение (25) переходит в уравнение эллиптического типа r2xΦ◦ + (ω2/a20)Φ◦ = 0,

называемое уравнением Гельмгольца.

9

При взаимодействии идеальной жидкости с непроницаемой границей области течения, в силу того что со стороны этой границы в направлении вектора n нормали к ней на частицы жидкости действует лишь давление, возможно относительное проскальзывание частиц,

т. е. в отличие от вязкой жидкости отсутствует эффект прилипания

частиц к границе. Поэтому на непроницаемых границах совпадают проекции векторов скорости идеальной жидкости и заданной скорости v◦ границы на направление нормали, т. е. v · n = v◦ · n, или (в случае безвихревого движения жидкости) (rxΦ) · n = v◦ · n. При построении математической модели (ММ) течения идеальной жидкости на ее свободной поверхности должно быть задано давление, а на проницаемых границах области — вектор скорости или давление.

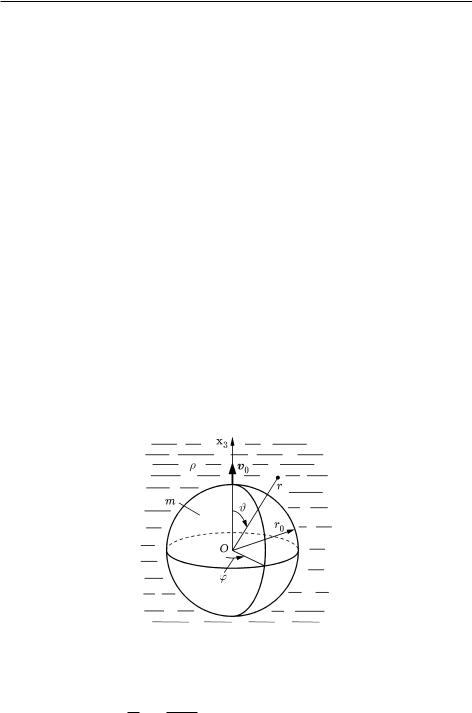
Пусть твердый шар радиусом r0 и массой m движется поступательно вдоль оси Ox3 со скоростью v0 в идеальной несжимаемой жидкости плотностью ρ0. Приняв обтекание шара безвихревым и осесимметричным относительно этой оси, представим (21) в подвижной системе сферических координат с началом в центре шара:

где r — радиальная координата; ϑ [0, π] — угол, отсчитываемый от положительного направления оси Ox3 (рис. 0.1).

Рис. 0.1

На поверхности S шара (при r = r0) ∂Φ/∂r = v0 cos ϑ, что дает основание искать решение (26) в виде Φ(r,ϑ) = R(r)cos ϑ, удовлетворяющем

(26) при условии drd r2 − 2R(r) = 0. Подставляя сюда R(r) =

= rk, находим k(k + 1) − 2 = 0, т. е. k1 = 1 и k2 = −2. Таким образом, R(r) = C1r + C2/r2. В случае C1 6= 0 при r → ∞ имеем R(r) → ∞, что

10

противоречит физическому смыслу, поскольку вдали от движущегося шара жидкость неподвижна. Поэтому C1 = 0, а вторую константу

Кинетическая энергия жидкости при движении шара с учетом (27) составит

где m = 2πρ0r3/3 — половина массы жидкости, вытесненной шаром. e 0

Суммарная кинетическая энергия системы «шар — жидкость» при поступательном движении шара будет KΣ = (m + m)v02/2. Изменение KΣ за время dt, согласно закону сохранения энергии, равно работе, со-

эквивалентна ММ поступательного движения в вакууме материальной точки массой m + me . В связи с этим величину me называют присоеди-

ненной массой шара.

При поступательном движении в жидкости твердого тела, ограниченного поверхностью вращения, вводят понятия продольной и поперечной присоединенной массы, а в случае произвольного движения тела произвольной формы влияние жидкости учитывают введением

тензора второго ранга коэффициентов присоединенных масс.

Если на поле скоростей, определяемое соотношениями (27), наложить поле с составляющими vr = −v0 cos ϑ и vϑ = v0 sinϑ вектора ско-

идеальной несжимаемой жидкостью, имеющей вдали от шара скорость