
- •Идентификация параметров математической модели датчика угловой скорости Учебно – методическое пособие
- •Содержание
- •Перечень сокращений
- •Введение
- •Выбор схемы датчика угловой скорости платформы малогабаритной поворотной установки мпу – 1
- •Программное обеспечение стенда
- •Воспроизведение сигнала.
- •Генерирование тестового сигнала
- •Спектральный анализ
- •Цифровая фильтрация сигнала
- •Функциональная схема стенда
- •Декомпозиция блока а0
- •Диаграмма а4 обработки сигнала
- •Декомпозиция блока а43. Обработка и анализ сигнала
- •Декомпозиция блока а432. Выбор фильтра
- •Декомпозиция блока а4323. Расчёт фильтра
- •Декомпозиция блока а433. Спектральный анализ
- •4. Идентификация параметров математической модели дус
- •4.1. Математическая модель дуСа
- •4.2. Алгоритм определения параметров (Алгоритм Качмажа)
- •4.3. Идентификация параметров
- •Список использованной литературы
Декомпозиция блока а4323. Расчёт фильтра
Данная диаграмма детализирует блок расчёта фильтра из предыдущей схемы. В этой схеме присутствуют блоки: масштабирование сигнала, расчёт отфильтрованного сигнала, обратное масштабирование. Блоки масштабирования и обратного масштабирования введены по той причине, что сигнал, снимаемый с АЦП, является целым числом в пределах от -2048 до +2048, а между истинным значением сигнала и величиной, снимаемой с АЦП, есть пропорциональность.
Таблица 6.
№ блока |
Функция блока |
Вход |
Выход |
Управ-ление |
Средства |
А4231 |
Масштабирование сигнала |
Исходный сигнал |
Исходный масштабирован-ный сигнал |
|
Процедура масштабирова-ния |
А4232 |
Расчёт отфильтрованного сигнала |
Исходный отмасштабиро-ванный сигнал, коэффициент передаточной функции, передаточная функция фильтра |
Исходный и отфильтрован-ный отмасштабиро-ванные сигналы |
|
Процедура расчёта отфильтрован-ного сигнала |
А2433 |
Обработанное масштабирование |
Исходный и отфильтрвоан-ный отмасштабирован-ные сигналы |
Исходный и отфильтрован-ный сигналы |
|
Процедура обратного масштабирова-ния |
Декомпозиция блока а433. Спектральный анализ
Раскрывает спектральный анализ функции: выбор участка для анализа (спектральный анализ производится не над всем сигналом, а лишь над необходимой его частью), масштабирование сигнала (проводится по причинам, описанным выше), преобразование Фурье, отображение спектра. Все эти действия позволяют выполнить процедуры выбора участка сигнала, масштабирования, преобразования Фурье и процедуру вывода спектра. Управлением являются действия пользователя по управлению выбором участка для анализа и отображению спектра.
Таблица 7.
№ блока |
Функция блока |
Вход |
Выход |
Управление |
Средства |
А4331 |
Выбор участка для анализа |
Исходный и отфильтрован-ный сигналы |
Выборка для анализа |
Управление выбором |
Процедура выбора участка |
А4332 |
Масштабиро-вание сигнала |
Выборка для анализа |
Масштабирован-ный сигнал |
|
Процедура масштабирова-ния |
4. Идентификация параметров математической модели дус
4.1. Математическая модель дуСа
Уравнение движения ДУС:
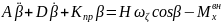 ,
,
где
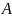 -
момент инерции гироблока относительно
оси прецессии,
-
момент инерции гироблока относительно
оси прецессии,
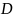 -
коэффициент демпфирования,
-
коэффициент демпфирования,
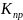 -
коэффициент угловой жесткости пружины,
-
коэффициент угловой жесткости пружины,
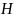 -
кинетический момент ротора гироскопа,
-
кинетический момент ротора гироскопа,
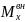 -
сумма внешних возмущающих моментов.
-
сумма внешних возмущающих моментов.
Также в входят вредные моменты вокруг оси и погрешности от перекрестных угловых скоростей, которыми можно пренебречь.
Из-за
малости угла
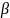 можно считать, что
можно считать, что
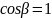 ,
тогда уравнение движения ДУС записывается
в следующем виде:
,
тогда уравнение движения ДУС записывается
в следующем виде:
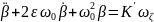 (1)
,
(1)
,
где
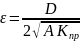 - коэффициент затухания системы,
- коэффициент затухания системы,
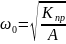 -
собственная круговая частота колебаний
системы,
-
собственная круговая частота колебаний
системы,
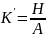 -
коэффициент усиления.
-
коэффициент усиления.
Уравнение движения (1) в переменных Лапласа будет выглядеть:
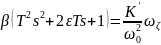 (2)
,
(2)
,
где
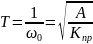 - постоянная времени системы.
- постоянная времени системы.
Так
как измеряется напряжение
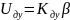 ,
то уравнение (2) будет перезаписано в
следующем виде:
,
то уравнение (2) будет перезаписано в
следующем виде:
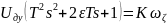 (3)
,
(3)
,
где
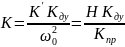 - коэффициент усиления.
- коэффициент усиления.
Уравнению движения ДУС соответствует следующая структурная схема:
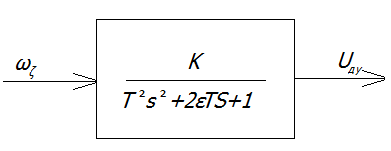
Рис.2.Структурная схема уравнения движения ДУС
Найдем решение уравнения движения (3). Для этого запишем характеристическое уравнение в общем виде:
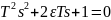 (4)
(4)
Начальные и граничные условия:
1)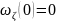
2)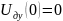
3)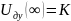
Корни характеристического уравнения равны:
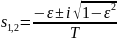 (5)
(5)
Из (5) следует, что решение уравнения (3) является зависимость:
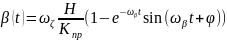 (6)
,
(6)
,
где
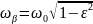 -
частота демпфированных колебаний.
-
частота демпфированных колебаний.
То
есть, собственное движение рамки прибора
будет представлять собой затухающие
колебания с частотой
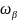 .
.
В
установившемся режиме
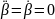 ,
тогда
,
тогда
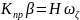 =>
=>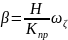 ,
то есть гироскопический момент от
движения основания
,
то есть гироскопический момент от
движения основания
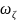 будет полностью уравновешиваться
противодействующим моментом пружины
и угол отклонения
будет пропорционален угловой скорости
вращения основания
.
будет полностью уравновешиваться
противодействующим моментом пружины
и угол отклонения
будет пропорционален угловой скорости
вращения основания
.
Для
определения переменной
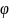 ,
используются начальные и граничные
условия:
,
используются начальные и граничные
условия:
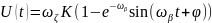
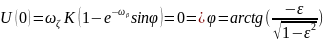
Следовательно,
в ходе идентификации необходимо
определить параметры
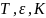 ,
чтобы в дальнейшем определить
,
чтобы в дальнейшем определить
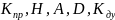 .
.
