
0096 / Термех вариант 16 / Lektsii_TM_zaochniki
.pdf
геометрической сумме моментов количеств движения всех точек системы относительно этого центра.
R |
n R |
R |
|
KO = ∑MO (mk Vk ). |
(16.3) |
||
k=1
Проекция вектора кинетического момента на какую-либо ось называется кинетическим моментом относительно данной оси.
Кинетический момент тела, вращающегося вокруг неподвижной оси OZ , находится по формуле:
Kz = Jzω , |
(16.4) |
где Jz момент инерции тела относительно оси вращения, ω – угловая скорость тела.
Теорема об изменении кинетического момента относительно центра (теорема моментов для системы): производная по времени от кинетического момента, взятого относительно некоторого неподвижного центра, равна сумме моментов всех внешних сил системы относительно того же центра:
dKO |
n |
R R |
|
|
= ∑MO (Fke ). |
(16.5) |
|||
|
||||
dt k=1 |
|
|
||
Данную теорему можно записать относительно координатных осей:
n R
dKx = ∑Mx (Fke ), dt k=1
dKy = ∑M y (Fke ), |
|
n |
R |
dt k=1
dKz |
n |
R |
|
|
= ∑Mz (Fke ). |
(16.6) |
|||
|
||||
dt k=1 |
|
|
||
Если тело вращается вокруг неподвижной оси OZ и при этом момент инерции относительно данной оси Jz остается постоянным, то с учетом (16.4) последнее равенство (16.6) можно записать в виде:
n |
R |
). |
|
&& |
e |
(16.7) |
|
Jzφ = ∑Mz (Fk |
|||
k=1
Равенство (16.7) называется дифференциальным уравнением вращательного движения твердого тела вокруг неподвижной оси.
Если сумма моментов, относительно некоторого центра, всех внешних сил, действующих на систему, равна нулю, то, как следует из (16.5), кинетический момент относительно того же центра остается постоянным по модулю и направлению.
n R R |
R |
|
∑MO (Fke )= 0 |
KO |
= const . |
k=1
31
Данное следствие выражает закон сохранения кинетического момента (момента импульса).
§17. Работа. Мощность.
Элементарной работой силы называется скалярная величина равная скалярному произведению вектора силы на вектор элементарного перемещения точки ее приложения.
|
|
dA = F drR |
|
|
(17.1) |
|
|
|
V |
Расписав |
скалярное произведение, |
||
|
F |
формулу (17.1) можно записать в виде: |
||||
|
|
|||||
D R |
|
|
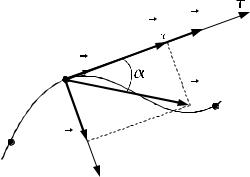
dA = Fcosα ds = Fτ ds, |
(17.2) |
||
M |
|
F |
где α– угол между вектором силы и ка- |
|||
|
|
сательной осью, Fτ = Fcosα |
|
|||
|
|
M 1 |
– проекция |
|||
M 0 F N |
|
|
силы F на касательную ось (рис. 17.1), |
|||
|
N |
|
ds – модуль элементарного перемеще- |
|||
|
|
|
||||
|
Рис. 17.1 |
|
ния точки. |
|
|
|
Расписав выражение (17.1) через проекции векторов, входящих в ска- |
||||||
лярное произведение, получим: |
|
|
|
|
||
|
|
dA = Fx dx + Fy dy + Fz dz . |
(17.3) |
|||
Работа силы на любом конечном перемещении М1М2 равна взятому |
||||||
вдоль этого перемещения интегралу от элементарной работы: |
|
|||||
|
|
M2 |
M2 |
R |
M2 |
|
|
|
AM1M2 = ∫ dA = ∫ |
F drR = |
∫ Fτ ds. |
(17.4) |
|
|
|
M1 |
M1 |
|
M1 |
|
Если сила остается постоянной по модулю и направлению (F = const ), то работа этой силы по перемещению точки вдоль некоторой траектории из положения М1 в положение М2 , равна:
A = F s cosα, |
(17.5) |
здесь s – кратчайшее расстояние между начальным и конечным положениями точки (длина вектора перемещения), α – угол между вектором силы и вектором перемещения.
Если угол α острый, то работа положительна, если угол α тупой, то работа отрицательна и если угол α = 90°, то работа силы равна нулю.
При вращении тела вокруг неподвижной оси OZ под действием силы
F , элементарная работа этой силы равна: |
|
dA = Mz (F) dφ . |
(17.6) |
32 |
|
При повороте тела на конечный угол φ1 , работа равна:
φ1 |
R |
|
A = ∫ |
Mz (F) dφ . |
(17.7) |
0 |
|
|
Если момент силы остается постоянным, то работа силы, при повороте тела на угол φ1 , равна:
A = Mz (F) φ1 . |
(17.8) |
Единицей измерения работы в СИ является джоуль 1Дж =1Н м.
Мощностью называется величина, равная работе, совершаемой силой за единицу времени.
|
dA |
R |
R |
R |
R |
|
|
N = |
= F |
dr |
= F |
V = F |
V . |
(17.9) |
|
|
|
||||||
|
dt |
|
dt |
|
τ |
|
|
|
|
|
|
|
|
Если тело вращается вокруг неподвижной оси OZ , то мощность, рав-
на:
|
dA |
|
R |
|
R |
|
|
N = |
= M |
(F) |
dφ |
= M |
(F) ω. |
(17.10) |
|
|
|
||||||
|
dt |
z |
|
dt |
z |
|
|
|
|
|
|
|
|
||
Единицей измерения мощности в СИ является ватт 1Вт =1Дж / с.
§18. Потенциальное силовое поле. Потенциальная энергия.
Часть пространства, в каждой точке которого на находящуюся там материальную точку действует некоторая сила, зависящая только от положения этой точки, называется силовым полем. Проекции силы поля на координатные оси являются некоторыми однозначными и непрерывными функциями от координат, т.е.
Fx = Fx (x, y,z), Fy = Fy (x, y,z), Fz = Fz (x, y,z).
Ели для данного силового |
поля |
существует функция |
координат |
|||||
Π(x, y,z) такая, что |
|
|
|
|
|
|
|
|
F = − ∂Π |
, |
F = − |
∂Π , |
F = − ∂Π |
, |
(18.1) |
||
x |
∂x |
|
y |
∂y |
z |
∂z |
|
|
|
|
|
|
|
|
|||
то данное силовое поле называется потенциальным. Функция Π называется потенциальной энергией данного силового поля, а силы, действующие в таком поле – потенциальными или консервативными.
Для выяснения физического смысла найдем выражение для элементарной работы силы потенциального поля. Согласно (17.3), имеем:
dA = F dx + F dy + F dz = − ∂Π dx + ∂Π dy + ∂Π dz = −dΠ , |
(18.2) |
|||||
x |
y |
z |
∂x |
∂y |
∂z |
|
|
|
|
|
|||
|
|
|
33 |
|
|
|

т.е. элементарная работа силы потенциального поля равна полному дифференциалу потенциальной энергии взятому со знаком минус. Тогда работа силы потенциального поля при перемещении точки из положения M1 в положение M2 равна:
M2 |
|
AM1M2 = − ∫ dΠ = Π1 − Π2 . |
(18.3) |
M1 |
|
Итак, работа силы потенциального поля равна разности потенциальных энергий в начальном и конечном положениях, и следовательно не зависит ни от вида, ни от длины траектории по которой перемещается точка.
Силы, работа которых зависит от вида траектории или от закона движения точки приложения силы, называют непотенциальными или неконсерввативными (например: сила трения, сила сопротивления среды).
Из (18.3) следует, что работа сил потенциального поля на всякой замкнутой траектории равна нулю.
Потенциальная энергия определена с точностью до произвольной постоянной. Чтобы определить эту постоянную считают в некоторой точке, называемой «нулевой точкой», потенциальная энергия равна нулю Π0 = 0 . Нулевую точку выбирают произвольно.
Потенциальную энергию в данном положении М1 также можно определить как работу, которую нужно совершить силам поля, чтобы переместить точку из данного положения в нулевое:
Π1 = AM1 0 . (18.4) Геометрическое место точек, в которых потенциальная энергия сохраняет постоянное значение, образует поверхность, которая называется экви-
потенциальной поверхностью или поверхностью уровня. Потенциальная энергия некоторых силовых полей:
1.Потенциальная энергия поля силы тяжести F = mg равна
Π= mgh.
2. Потенциальная энергия поля гравитационной силы F = G m1m2 r2
равна
Π = −G m1m2 . r
Нулевая точка находиться в бесконечности.
34

3. Потенциальная энергия поля силы упругости F = −cx равна
2
Π = cx . 2
За нулевую точку взята x = 0 .
§19. Теорема об изменении кинетической энергии. Закон сохранения энергии.
Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости.
Кинетической энергией материальной системы называется сумма кинетических энергий всех точек, входящих в систему:
|
1 |
|
n |
|
||
T = |
∑mk Vk2 . |
(19.1) |
||||
|
|
|||||
|
2 k=1 |
|
||||
Кинетическая энергия тела при поступательном движении: |
|
|||||
T = |
1 |
mV2 . |
(19.2) |
|||
|
||||||
2 |
|
|
||||
Кинетическая энергия тела при вращении вокруг неподвижной оси
:
T = |
1 |
J ω2 . |
(19.3) |
2 |
z |
|
Кинетическая энергия тела при плоскопараллельном движении:
T = |
1 |
mV2 |
+ |
1 |
J |
|
ω2 |
, |
(19.4) |
|
|
zc |
|||||||
|
2 |
c |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|||
здесь Vc – скорость центра масс, Jzc – момент инерции, относительно оси проходящей через центр масс, перпендикулярной плоскости движения тела.
Теорема об изменении кинетической энергии системы в интегральной форме: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.
n |
n |
|
T1 − T0 = ∑Ake + ∑Aki , |
(19.5) |
|
k=1 |
k=1 |
|
здесь T0 – начальная кинетическая энергия системы, T1 – конечная кинетическая энергия системы.
35
Если система неизменяемая, т.е. такая система в которой расстояние между каждыми двумя взаимодействующими точками остается во все время движения постоянными, то сумма работ всех внутренних сил равна нулю, и теорема (19.5) запишется:
n |
|
T1 −T0 = ∑Ake . |
(19.6) |
k=1 |
|
Если все действующие на систему внешние и внутренние силы потен- |
|
циальны, то, согласно (18.3) можно записать: |
|
∑Ak = Π0 − Π1 , |
|
сравнение с формулой (19.5), даёт: |
|
T1 + Π1 = T0 + Π0 = const . |
(19.7) |
Следовательно, при движении под действием |
потенциальных сил |
сумма кинетической и потенциальной энергий системы в каждом ее положении остается величиной постоянной. В этом и состоит закон сохранения механической энергии.
Величина E = T + Π называется полной механической энергией системы.
§20. Принцип Даламбера. Уравнения кинетостатики.
Рассмотрим движение точки под действием сил, равнодействующую
которых обозначим F , и запишем для нее второй закон Ньютона:
R
F = ma ,
|
R |
|
введя обозначение |
Fu = −ma , |
(20.1) |
получим: |
|
|
|
F + Fи = 0. |
(20.2) |
Вектор Fи , равный по модулю произведению массы точки на ее ускорение и направленный противоположно вектору ускорения, называется силой инерции.
Равенство (20.2) представляет собой Принцип Даламбера для точки: если в любой момент времени ко всем действующим на точку силам прибавить силу инерции, то полученную систему сил формально можно считать уравновешенной и применять к ней уравнения статики.
Рассмотрим систему из n материальных точек. Обозначив Fki – сумму всех действующих на k -ую точку внутренних сил, Fke – сумму всех дей-
36
ствующих на k -ую точку внешних сил и составив для каждой точки равенство (20.2), получим:
Fe + Fi + Fи = 0, k = |
1,n |
. |
(20.3) |
k k k |
|
||
Данное равенство, выражает принцип Даламбера для системы: если в любой момент времени к каждой из точек системы помимо действующих на нее внешних и внутренних сил прибавить силы инерции, то полученную систему можно формально считать уравновешенной и применять к ней уравнения статики.
Уравнения кинетостатики позволяют решать задачи динамики, составляя уравнения в таком же виде, как это делается в статике. Они аналогичны уравнениям статики.
|
|
|
|
Re + Rи = 0, Re |
+ Rи = 0, Re + Rи = 0, |
|
||||
|
|
|
|
x |
x |
y |
y |
z |
z |
(20.4) |
|
|
|
|
M e + M и = 0, |
M e + M и = 0, |
M e + M и = |
||||
|
|
|
|
0, |
||||||
|
|
|
|
x |
x |
y |
y |
z |
z |
|
здесь Rxи , Ryи , Rzи |
проекции на оси координат главного вектора сил инерции |
|||||||||
R |
n |
R |
|
|
|
|
|
|
|
|
Rи = ∑Fkи , Mxи , |
Myи , Mzи |
проекции на оси координат главного момента сил |
||||||||
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
R |
n |
R R |
|
|
|
|
|
|
инерции |
M и = ∑MO Fkи . |
|
|
|
|
|
|
|||
k=1
Главный вектор сил инерции механической системы (твердого тела) равен произведению массы системы (тела) на ускорение центра масс и направлен противоположно этому ускорению.
R
Rи = −mac . (20.5)
Главный момент сил инерции механической системы (твердого тела) относительно некоторого центра O равен, взятой со знаком минус, производной по времени от кинетического момента системы (тела), относительно того же центра.
R |
dKo |
|
|
|
M и = − |
. |
(20.6) |
||
|
||||
o |
dt |
|
||
|
|
|||
1.При поступательном движении силы инерции твердого тела приводятся к равнодействующей (20.5) проходящей через центр масс тела и направленной в сторону, противоположную ускорению.
2.При вращении вокруг оси, проходящей через центр масс тела, система сил инерции тела приводится к одной только паре с моментом, по модулю равным
37
M и |
= J |
cz |
ε, |
(20.7) |
cz |
|
|
|
инаправленным противоположно угловому ускорению ε .
3.При плоскопараллельном движении, если тело имеет плоскость симметрии и движется параллельно этой плоскости, то, система сил инерции тела приводится к силе (20.5) приложенной в центре масс тела, и паре
сил с моментом (20.7).
§21. Связи. Принцип возможных перемещений. Общее уравнение динамики.
Система материальных точек называется свободной, если положения отдельных ее точек и их скорости могут принимать произвольные значения. В противном случае система называется несвободной.
Любого вида ограничения, которые налагаются на положения и скорости точек механической системы называются связями, которые выполняются независимо от того, какие на систему действуют силы.
Связи, которые описываются уравнениями, называются удерживающими (налагаемые ими ограничения сохраняются при любом положении системы). Например: шарнирная опора.
Связи, описание которых осуществляется с помощью неравенств, называются неудерживающими (от таких связей система может «освобождаться»). Например: нить, поверхность.
Связи, налагающие ограничения на координаты и скорости точек системы и выражаемые аналитически уравнениями вида
f (t,x1, y1,z1, …,xn , yn ,zn ,x&1, y&1,z&1, …,x&n , y&n ,z&n ) = 0 носят общее название кинематических.
Если время не входит в уравнение (или неравенство) связи в явном виде, то связь называется стационарной. Если же связь зависит от времени явно, то она называется нестационарной.
Кинематические связи, уравнения которых не содержат скоростей или путем интегрирования могут быть к такому виду приведены, называются
голономными, в противном случае – неголономными.
Возможным (виртуальным) перемещением данной системы называется всякое элементарное перемещение ее точек, допускаемое в данный момент времени наложенными на систему связями.
Возможное перемещение точки обозначают символом δr а δx, δy, δz –
проекции его на координатные оси.
38
Символом δ обозначают вариацию функции – это бесконечно малое приращение некоторой функции f (t,x, y,z), вычисляемое в предположении, что аргумент t является фиксированным параметром, а x, y, z представляют изменяющиеся независимо от t величины. Формально вариация вычисляется так же как дифференциал.
При стационарных связях действительное перемещение любой точки системы, совпадает с одним из возможных перемещений. При нестационарных связях действительное не совпадает ни с одним из возможных перемещений.
Число независимых между собой возможных перемещений механической системы называются числом степеней свободы этой системы.
Возможной работой называется элементарная работа, которую действующая на материальную точку сила могла бы совершить на возможном перемещении этой точки
R
δA = F δr . (21.1) Идеальными называются связи, для которых сумма элементарных ра-
бот их реакций на любом возможном перемещении системы равна нулю
n |
n |
R |
δrR = 0 . |
∑δAkN = ∑Nk |
|||
k=1 |
k=1 |
|
|
Принцип возможных перемещений: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю:
n |
n R |
R |
= 0. |
|
∑δAka = ∑Fka δr |
(21.2) |
|||
k=1 |
k=1 |
|
|
|
Активной называется сила, которая начав действовать на покоящееся тело, может привести его в движение.
Этот принцип дает общий метод решения задач статики для систем с идеальными голономными связями. Причем уравнение в (21.2) не входят наперед неизвестные реакции связи, что существенно упрощает решение.
Принцип возможных перемещений дает общий метод решения задач статики. С другой стороны, принцип Даламбера позволяет использовать методы статики для решения задач динамики. Следовательно, применяя эти два принципа одновременно, можно получить общий метод решения задач динамики.
39
Принцип Даламбера – Лагранжа: при движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю.
∑δAka + ∑δAkи = 0, |
(21.3) |
где ∑δAka – сумма возможных работ всех активных сил системы, ∑δAkи –
сумма возможных работ всех сил инерции системы. Уравнение (21.3) называется общим уравнением динамики.
§22. Обобщенные координаты. Уравнение Лагранжа второго рода.
Независимые между собой параметры любой размерности, число которых равно числу степеней свободы системы и которые однозначно определяют ее положение, называют обобщенными координатами системы. Обозначаются обобщенные координаты буквой q. Тогда положение системы, имеющей s степеней свободы, будет определяться s обобщенными координатами
q1, q2 ,…, qs .
Первые производные от обобщенных координат по времени называются обобщенными скоростями, и обозначаются:
q&1, q&2 ,…, q&s .
Вторые производные от обобщенных координат по времени называются обобщенными ускорениями, и обозначаются:
q&&1, q&&2 ,…, q&&s .
Так как положение системы однозначно определяется обобщенными координатами, а положение каждой точки системы определяется ее радиусвектором, то его можно выразить через обобщенные координаты:
R |
R |
|
|
|
|
|
|
|
|
|
|
,q2 ,…qs ), |
k =1,n . |
|
|||||||||
rk = rk (q1 |
(22.1) |
||||||||||
Перейдем к определению обобщенных сил, для этого запишем вариа- |
|||||||||||
цию радиус-вектора через вариации обобщенных координат |
|
||||||||||
|
s |
|
R |
|
|
|
|
|
|
||
δrRk |
|
∂rk |
|
|
|
|
|
|
|
||
= ∑ |
δqj , |
k = |
1,n |
|
(22.2) |
||||||
|
|||||||||||
|
j=1 |
|
∂qj |
|
|
|
|
|
|
||
и подставим в выражение для возможной работы всех активных сил:
n |
R |
n |
R |
s |
R |
||
∂rk |
|
||||||
δAa = ∑Fka δrRk |
= ∑Fka ∑ |
δqj , |
|||||
|
|||||||
k=1 |
|
k=1 |
|
j=1 |
∂qj |
||
или меняя порядок суммирования
40
