0075 / DM_3_rabota

РАСЧЕТ ОТКРЫТОЙ КОНИЧЕСКОЙ

ПЕРЕДАЧИ

Рассчитать открытую коническую передачу по заданной схеме (зацепление внешнее, передача прямозубая).

Исходные данные для расчёта

1. Мощность на ведущем валу P₂=9419,4 Вт.

2. Частота вращения ведущего вала n₂=486,67 .

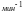3. Передаточное число u = 2,781.

4. Долговечность передачи 5 лет.

5. Возможные перегрузки

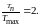
5.1 Выбор материала зубчатых колес, вида их термической обработки (таблица 1).

Материалы и термическая обработка зубчатых колес:

шестерня - сталь 45, улучшение, НВ₂ = 192…240, для расчета НВ₂ = 220;

колесо - сталь 45, нормализация HB₃=170…217, для расчета HB₃=210.

5.2 Механические характеристики материала (таблица 1)

шестерня: предел прочности - _в2=750 МПа,

предел текучести - _т2=450 МПа;

колесо: предел прочности - _в3=600 МПа,

предел текучести - _т3=340 МПа.

5.3 Определение допускаемых напряжений

5.3.1 Допускаемые напряжения изгиба шестерни 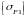(МПа) вычисляют по формуле (1)

[σ_F]₂ = σ_Flim2*Y_N2*Y_A2/S_F2 ,

где σ_Flim2 =1,8HB₂ = 1,8*220 = 396 МПа;

Y_N2 = 1;

Y_A2 = 0,65;

S_F2 = 1,75.

[σ_F]₂ = 396*1*0,65/1,75 = 147 МПа.

Допускаемые напряжения изгиба колеса [σ_F]₃ вычисляют по формуле (1)

[σ_F]₃ = σ_Flim3*Y_N3*Y_A3/S_F3,

где σ_Flim3 =1,8HB₃ = 1,8*210 = 378 МПа;

Y_N3 = 1;

Y_A3 = 0,65;

S _F3 = 1,75.

[σ_F]₃ = 378*1*0,65/1,75 = 140 МПа.

5.3.2 Предельные допускаемые напряжения изгиба при кратковременных перегрузках.

Допускаемые напряжения для проверки прочности зубьев шестерни при перегрузках [σ_F]_max2 (МПа) вычисляют по формуле (5)

[σ_F]_max2 = σ_Flim2*Y_Nmax2*K_st2/S_st2 ,

где Y_Nmax2 = 4;

S_st2 =2;

[σ_F]_max2 = 396*4*1,3/2 = 1,03*10³ МПа.

Допускаемые напряжения для проверки прочности зубьев колеса при перегрузках [σ_F]_max3 (МПа) вычисляют по формуле (5)

[σ_F]_max3 = σ_Flim3*Y_Nmax3*K_st3/S_st3 ,

где Y_Nmax3 = 4;

S_st3 = 2;

[σ_F]_max3 = 378*4*1,3/2 = 982,8 МПа.

5.4 Проектный расчет

5.4.1 Угловая скорость ведущего вала ω₂, ( )

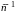Угловая скорость ведущего вала вычисляется по формуле (6)

ω₂ = π*n₂/30;

ω₂ = 3,14*486,67/30 = 50,96 c^-1.

5.4.2 Вращающие моменты на валах

Вращающий момент на ведущем валу T₂ (Н∙м) вычисляют по формуле (7)

T₂ = 184,83 Н∙м.

Вращающий момент на ведомом валу T₃ (Н∙м) вычисляют по формуле (8)

T₃ = 464,28 Н∙м.

5.4.1 Число зубьев шестерни z₂ и колеса z₃

Число зубьев шестерни z₂ = 18;

Число зубьев колеса z₃ вычисляют по формуле (9)

z₃ = z₁*u;

z₃ = 18*2,781 = 50.

Действительное передаточное число вычисляется по формуле (10)

u = z₃/z₂;

u = 50/18 = 2,78.

5.4.4 Угол делительного конуса шестерни 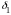и колеса

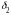
Угол делительного конуса шестерни и колеса вычисляется по формулам (11)

δ₃ = arctg u;

δ₃ = arctg 2,78 = 70˚13`;

δ₂ = 90˚ – δ₃;

δ₂ = 19˚47`.

5.4.5 Приведенные числа зубьев шестерни 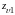и колеса

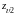
Приведенные числа зубьев шестерни и колеса вычисляются по формулам (12)

z_υ2=z₂/cosδ₂;

z_υ2=19,09;

z_υ3=z₃/cosδ₃;

z_υ3=147,2.

5.4.6 Коэффициент, учитывающий форму зуба

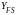
Коэффициент, учитывающий форму зуба, определяется по рис. 3

- для шестерни

Y_FS2 = 4,2;

- для колеса

Y_FS = 3,75.

5.4.7 Коэффициент ширины венца зуба конической шестерни относительно диаметра Ψ_bd = b₂/d₂

Коэффициент ширины венца зуба конической шестерни относительно диаметра Ψ_bd = b₂/d₂ принимается по таблице 4 - 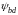= 0,4.

5.4.8 Коэффициент концентрации нагрузки при расчете на изгиб

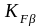
Коэффициент концентрации нагрузки при расчете на изгиб определяется по зависимости (13)

,

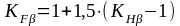где 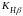=1,09.

.

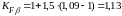5.4.9 Ориентировочное значение внешнего торцевого модуля 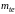(мм)

Ориентировочное значение внешнего торцевого модуля (мм) вычисляют по формуле (14)

,

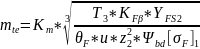где 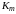= 14;

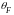= 0,85.

m_te = 5,12 мм.

Полученное значение модуля округляем до большего значения из стандартного ряда (таблица 5) - = 6 мм.

5.4.10 Внешнее конусное расстояние 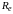, мм

Внешнее конусное расстояние определяется по формуле (15)

R_e = 0,5*m_te*z₂ / sin δ₂ ;

R_e = 159,54 мм.

5.4.11 Ширина венца зубчатых колес b, мм

Ширина венца зубчатых колес определяется по формуле (16)

;

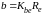b = 0,285*159,54 = 45,47 мм.

Величина b округляется до стандартного значения по таблице 6, b =45 мм.

5.4.12 Среднее конусное расстояние 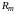, мм

Среднее конусное расстояние определяется по формуле (17)

;

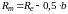R_m = 159,54 – 0,5*45 = 137,04 мм.

5.4.13 Внешние диаметры колес, мм

- делительные диаметры шестерни d_e2 и колеса d_e3 определяются по формулам (18)

d_e2 = m_te*z₂;

d_e2 = 6*18 = 108 мм;

d_e3 = m_te*z₃;

d_e3 = 300 мм;

- диаметры окружностей вершин зубьев шестерни d_ae2 и колеса d_ae3 вычисляются по формулам (19)

d_ae2 = d_e2 + 2*m_te*cos δ₂;

d_ae2 = 119,28 мм;

d_ae3 = d_e3 + 2*m_te*cos δ₃;

d_ae3 = 304,08 мм;

- диаметры окружностей впадин шестерни зубьев шестерни d_fe2 и колеса d_fe3 вычисляются по формулам (20)

d_fe2 = d_e2 – 2,4*m_te*cos δ_2;

d_fe2 = 94,464 мм;

d_fe3 = d_e3 – 2,4*m_te*cos δ₃;

d_fe3 = 295,104 мм.

5.4.14 Параметры колес в среднем сечении, мм

- средний модуль вычисляется по формуле (21)

;

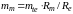m_m = 6*137,04/159,54 = 5,154 мм;

- средние делительные диаметры шестерни d_m2 и колеса d_m3 определяются по формулам (22)

d_m2 = m_m*z₂ = 92,772 мм;

d_m3 = m_m*z₃ = 257,7 мм.

5.4.15 Определение окружной скорости 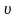и назначение степени точности передачи

Окружная скорость вычисляется по формуле (23)

υ = π*d_m2*n₂ / 60;

υ = 3,14*0,092772*486,67/60 = 2,37 м/c.

По таблице 7 принимаем 8-ю степень точности.

5.5 Проверочный расчет

5.5.1 Проверочный расчет на выносливость зубьев при изгибе проводится по тому из колес пары, для которого меньше отношение .

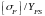Для шестерни [σ_F]₂/Y_FS2 = 147/4,2 = 35;

Для колеса [σ_F]₃/Y_FS3 = 140/3,75 = 37,33.

Дальнейший расчет ведем для шестерни.

Напряжение изгиба 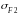(МПа) по формуле (24)

σ_F2­­­­­ = Y_FS2*F_t2*K_F / θ_F*b*m_m⋜ [σ_F]₂ ,

где F_t = 2*10³*T₂ / d_m2;

;

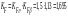σ_F2­­­­­ = 91,68 ⋜ [σ_F]₂ .

σ_F3 = Y_FS3*F_t3*K_F / θ_F*b*m_m⋜ [σ_F]_3;

σ_F3 = 74,02 ⋜ [σ_F]₃.

Т.к. условие σ_F­­­­­ ⋜ [σ_F] выполняется, передача работоспособна.

5.5.2 Проверочный расчет на заданную кратковременную перегрузку

Максимальные напряжения изгиба определяют по формуле (25)

σ_Fmax2 = σ_F2(T_пик/T_max) ⋜ [σ_F]_max2,

где 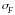, 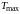- напряжение и максимальный из моментов учитываемые при расчете на усталость;

σ_Fmax2 = 183,36 ⋜ [σ_F]_max2;

σ_Fmax3 = σ_F3(T_пик/T_max) ⋜ [σ_F]_max3;

σ_Fmax3 = 148,04 ⋜ [σ_F]_max3.

Т.к. условие выполняется, передача выдерживает нагрузку и считается работоспособной.