2 Проектные и проверочные расчеты передач редуктора

Исходные данные к расчету: - срок службы передачи, (ч), (Н*м), (Н*м), (мин^-1), (мин^-1), . На рисунке 3 изображены разные виды зубчатых цилиндрических передач, на рисунке 4 изображен чертеж цилиндрического зубчатого колеса.

а) б) в) г)

Рисунок 3 - Цилиндрические зубчатые передачи: а) прямозубая; б) косозубая;

в) шевронная; г) прямозубая внутреннего зацепления

Зубчатое колесо передачи, имеющее меньшее число зубьев называется шестерней, большее число зубьев - колесом. Чертеж зубчатого колеса представлен на рисунке 2.

Рисунок 4 - Чертеж цилиндрического зубчатого колеса

2.1 Выбор материала конической шестерни и конического колеса

Режим нагружения - типовой: средний нормальный. Подобраны материалы зубчатых колес и их механические характеристики:

- шестерня - 40ХН по ГОСТ 4543-71, термообработка - улучшение,

(размер сечения заготовки - 100 мм)

- колесо - 40ХН по ГОСТ 4543-71, термообработка - улучшение,

(размер сечения заготовки - 100 мм)

(МПа) - предел прочности материала шестерни;

(МПа) - предел прочности материала колеса;

(МПа) - предел текучести материала шестерни;

(МПа) - предел текучести материала колеса;

- твердость поверхности материала шестерни в ед. HB;

- твердость поверхности материала колеса в ед. HB;

Частота вращения вала шестерни ( ):

n1=63,3*5=316,5 (об/мин)

2.2 Проектный и проверочный расчеты на контактную выносливость активных

поверхностей зубьев

2.2.1 Предел контактной выносливости материалов шестерни и колеса ( ) вычисляется по формуле [2.1] и [2.2]:

[2.1]

(МПа)

[2.2]

(МПа)

2.2.2 Коэффициент запаса прочности ( ):

- для колес с однородной структурой материала

2.2.3 Базовое число циклов напряжений, соответствующее пределу выносливости ( ):

- число циклов (расчетное значение);

Исходя из условия:

- число циклов (принятое значение);

- число циклов (расчетное значение);

- число циклов (принятое значение);

2.2.4 Показатель степени кривой усталости при расчете на изгибную выносливость ( ):

- для зубчатых колес с однородной структурой материала, включая закаленные при нагреве ТВЧ со сквозной закалкой, и зубчатых колес со шлифованной переходной поверхностью, независимо от твердости и термообработки их зубьев

2.2.5 Коэффициенты, характеризующие интенсивность нагружения ( , ):

Режим нагружения средний равновероятный.

- коэффициенты для шестерни;

- коэффициенты, принятые для колеса;

2.2.6 Эквивалентное число циклов напряжений при расчете контактной выносливости ( )

- суммарное число циклов нагружения зубьев шестерни;

- суммарное число циклов нагружения зубьев колеса;

- эквивалентное число циклов нагружения зубьев шестерни;

- эквивалентное число циклов нагружения зубьев колеса;

2.2.7 Коэффициент долговечности при расчете на контактную выносливость ( )

Исходя из выбранного по условию выражения [2.3], определим значение коэффициента долговечности ( ):

[2.3]

Расчетное значение коэффициента долговечности для шестерни:

Расчетное значение коэффициента долговечности для колеса исходя из формулы [2.3]:

По условиям 0,75 ≤ Z_{N пр £}Ј 2,6 - для однородной структуры материала, 0,75 ≤ Z_{N пр £}Ј 1,8 - для поверхностного упрочнения, выбираем принятое значение коэффициента долговечности.

- принятое значение коэффициента долговечности для шестерни;

- принятое значение коэффициента долговечности для колеса.

2.2.8 Допускаемое контактное напряжение, не вызывающее опасной контактной усталости

материала

Для шестерни:

_(МПА)

Для колеса:

(МПа)

2.2.9 Расчетное допускаемое контактное напряжение ( )

(МПа)

(МПа) - принятое значение расчетного допускаемого контактного напряжения.

2.2.10 Коэффициент ширины ( ) по ГОСТ 2185-66

2.2.11 Вспомогательный коэффициент, принимаемый для стальных зубчатых колес ( )

2.2.12 Коэффициент ширины

2.2.13 Предельное значение коэффициента ширины ( )

2.2.14 Коэффициент, учитывающий неравномерность распределения нагрузки по длине

контактных линий ( )

- для шестерни, расположенной относительно опор симметрично;

2.2.15 Рассчетная величина межосевого расстояния ( )

2.2.16 Принятое межосевое расстояние по ГОСТ 2185-66 ( )

2.2.17 Рассчетное значение рабочей ширины венца зубчатого колеса ( )

2.2.18 Рабочая ширина венца (принятое значение по ГОСТ 6636-69, ряд Ra20) ( )

2.2.19 Ориентировочное значение модуля зацепления ( )

2.2.20 Модуль зацепления (принятое значение по ГОСТ 9563-60) ( )

2.2.21 Предварительное значение угла наклона зубьев ( )

Д

2.2.22 Ориентировочное значение суммарного числа зубьев передачи ( ) при х1=х2=0

зубьев

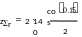
2.2.23 Cуммарное число зубьев (принятое значение) ( )

2.2.24 Угол наклона зубьев (уточненное расчетное значение) ( )





град

2.2.25 Проверка условия достаточности ширины

мм

Таким образом условие достаточности ширины выполняется.

2.2.26 Число зубьев шестерни ( )

зубьеврасчетное значение

2.2.27 Число зубьев колеса ( )

2.2.28 Передаточное число передачи (фактическое значение)



2.2.29 Проверка отклонения фактического передаточного числа передачи от стандартного

%



2.2.30 Окружная скорость ( )

)

м/с)

2.2.31. Степень точности передачи по ГОСТ 1643-81 ( )

2.2.32. Коэффициент торцевого перекрытия ( )

)



2.2.33 Коэффициент осевого перекрытия ( )

)



2.2.34 Суммарный коэффициент перекрытия ( )

2.2.35 Коэффициент, учитывающий суммарную длину контактных линий ( )

2.2.36 Коэффициент, учитывающий распределение нагрузки между зубьями ( )

2.2.37 Коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении ( )

2.2.38 Расчетное контактное напряжение

- данное условие выполняется

2.3 Проверочный расчет на выносливость при изгибе зубьев

2.3.1 Предел выносливости материала зубьев при изгибе, соответствующий базовому

числу циклов напряжений ( )

1=1.75·300=525 МПа – для шестерни

2=1.75·270=472.5 МПа –для колеса

2.3.2 Базовое число циклов напряжений (число циклов, соответствующее на диаграмме

усталости переходу наклонного участка кривой усталости в горизонтальный участок

или участок с очень малым наклоном к оси циклов) ( )

- циклов

2.3.3 Эквивалентное число циклов ( )

2.3.4 Коэффициент долговечности при расчете на выносливость при изгибе ( )

- принятые значения для шестерни и колеса;

2.3.5 Коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении

( )

2.3.6 Коэффициент, учитывающий неравномерность распределения нагрузки по длине

контактных линий

2.3.7 Коэффициент, учитывающий распределение нагрузки между зубьями ( )

2.3.8 Коэффициент, учитывающий внешнюю динамическую нагрузку ( )

2.3.9 Коэффициент перегрузки ( )

2.3.10 Эквивалентное число зубьев ( )

)

3

)

3

2.3.11 Коэффициенты смещения (х)

2.3.12 Коэффициент, учитывающий форму зуба и концентрацию напряжений ( )

1 = 3.999

2= 3.579

2.3.13 Коэффициент, учитывающий наклон зуба ( )

=1- 1.415·0.1593· 0.892

2.3.14 Коэффициент, учитывающий перекрытие зубьев при >1 ( )

2.3.15 Коэффициент, учитывающий влияние двухстороннего приложения нагрузки ( )

- при двустороннем приложении нагрузки для зубчатых колес из нормализованной или улучшенной стали

2.3.16 Коэффициент запаса прочности ( )

- принятые значения, соответственно для шестерни и колеса

2.3.17 Допускаемое напряжение при изгибе ( )

2.3.18 Допускаемое напряжение при расчете на изгибную выносливость ( )

=180.662 (МПа) - принятое значение

2.3.21. Напряжение изгиба ( )

ss_F=

ss_F=

2.4 Расчет геометрических параметров зубчатых колес и усилий, действующих в

зацеплении (при х1=х2=0)

2.4.1 Делительные диаметры (d)

)

 

)



2.4.2 Диаметры окружностей вершин ( )

1=48.617+2·2=52.617(мм)

2=324.978+2·2=328.978(мм)

2.4.3 Диаметры окружностей впадин ( )

1=48.617-2.5·2=43.617(мм)

2=234.978-2.5·2=229.978(мм)

2.4.4 Ширина шестерни ( )

=56+2=58(мм) – расчетное значение

2.4.5 Окружное усилие ( )

2.4.6 Радиальное усилие ( )

975 (Н)

2.4.7 Осевое усилие ( )

=425 (Н)

2.4.8 Консольная нагрузка вызывается муфтой, соединяющими редуктор с рабочей машиной.

Консольная сила от муфты определяется по формулам:

На тихоходном валу F_М2, Н:

где Т₂ – вращающий момент на тихоходном валу, Н∙м

На рисунке 5 дана cхема усилий, действующих на валы редуктора.

Рисунок 5 а- Схема усилий, действующих на валы редуктора

Параметры	Шестерня	Колесо
Ft,H	2646	2646
Fr, H	975	975
Fa,H	425	425
FM, H	-	2204
Т, H/м	63.99	310.9

2.5 Расчет валов

Редукторный вал представляет собой ступенчатое цилиндрическое тело, количество и размеры ступеней которого зависят от количества и размеров установленных на вал деталей.

2.5.1 Выбор материала для валов

Выберем для валов сталь 40Х по ГОСТ 4543-71 улучшенная с механическими характеристиками

2.5.2 Определение диаметров тихоходного вала

Определяем диаметр выходного конца вала под полумуфтой из расчёта на чистое кручение

где [τ_к]=(20…40) (Мпа)

Принимаем [τ_к]=30 (Мпа).

;

Согласовываем d₁с диаметром цепной муфты , для этого определяем расчетный момент, передаваемый муфтой:

Т_м=Т₂К, где К – коэффициент, учитывающий условия эксплуатации привода. К=1,3…1,5

Принимаем К=1,5

Т_м=310,91,5=466,35 (Н∙м).

Необходимо соблюдать условие Т_м<[T], где [T] – допускаемый момент, передаваемый муфтой

В нашем случае необходимо принять [Т] 500(Н∙м)

Тогда принимаем окончательно

d_м2=40(мм);

l_м2=57(мм). (Длина полумуфты) Тип 2, исполнение 2.

Проверяем возможность соединения валов стандартной муфтой

;

; (мм).

Так как соединение валов стандартной муфтой возможно.

Принимаем окончательно с учетом стандартного ряда размеров R_а40:

(мм)

d₂ = d₁ + 2×t – диаметр вала под утопление крышки с отверстием и подшипник

d_{2 =42 (мм)}-принятое значение

_l2 » 1.5×d₂ - длина вала под утопление крышки с отверстием и подшипник

_{l2= 63(мм)}

d₃ = d₂ + 3.2×r- диаметр вала под колесо

d_{3=42+3·2.5=49.5(мм)}

d_{3=50 (мм) – принятое значение}

d₄ = d_{2 -} диаметр вала под подшипник

d₄ =42(мм)

l₄=B - для шариковых подшипников, где B-ширины подшипников опор

Намечаем приближенную конструкцию ведомого вала редуктора.

Рис. 6- Приближенная конструкция ведомого вала

2.5.3 Эскизная компоновка ведомого вала

Назначаем предварительно подшипники шариковые радиальные однорядные 209

Определим основные параметры подшипников:

Подшипник 209 ГОСТ 8338-75

Размеры: d=45(мм), D=85(мм), B=19(мм), r=2(мм)

Грузоподъемность: С_{r=33.2(кН),} С_{r0=18.6(кН)}

a b c

L

Рис.7 Эскизная компоновка ведомого вала

Выполняем эскизную компоновку вала редуктора. Необходимо определить длину вала L и расстояния от середины подшипников до точек приложения нагрузок a, b и с (рис.7).

е=(8…12)мм – расстояние от торца подшипника до внутренней стенки корпуса редуктора;

К=(10-15)мм – расстояние от внутренней стенки корпуса до торца зубчатого колеса.

Принимаем

l_ст=s+10мм – длина ступицы колеса:

s=(30…50)мм - расстояние от торца подшипника до торца полумуфты.

Принимаем 40мм.

l_ст=40+10=50мм;

Определяем размеры а, b, с и L.

В= 20(мм)

а=b=В/2+е+К+lст/2;

а=b=20/2+10+11+50/2;

а=b=56мм

Принимаем а=b=56мм.

с= В/2+40+lм/2;

с=20/2+40+57/2;

с=78,5мм

Принимаем с=79мм.

L=В/2+a+b+c+ lм/2;

L=20/2+56+56+79+57/2;

L=229,5мм;

Принимаем L=230мм.

2.5.4 Расчет ведомого вала на изгиб с кручением

Определяем реакции в подшипниках в вертикальной плоскости.

m_Ау=0

-R_By·(a+b)+F_r·a- Fad/2 =0

R_By=(F_r·а- Fad/2)/ (a+b);

R_By= (975·0,056-425∙0,235/2)/0,112=42(Н)

Принимаем R_By=42(Н)

m_Ву=0

R_Аy·(a+b)-F_r·b- Fad/2=0

R_Аy=(F_r·b+ Fad/2)/ (a+b);

R_Аy =(975·0,056+425∙0,235/2)/ 0,112 =933,1(Н)

Принимаем R_Аy=933Н

Проверка: F_Ку=0

R_Аy- F_r+ R_By=933-975+42=0

Назначаем характерные точки 1,2,2’,3 и 4 и определяем в них изгибающие моменты:

М_1у=0;

М_2у= R_Аy·а;

М_2у=933·0,056 =52,2(Н·м);

М_2’у= М_2у- Fad/2 (слева);

М_2’у=52,2-425∙0,235/2=2,3(Н·м);

М_3у=0;

М_4у=0;

Строим эпюру изгибающих моментов М_у, Н∙м (рис.8)

Рассматриваем горизонтальную плоскость (ось х)

m_Ах=0;

R_Вх·(a+b)- F_t·a=0;

R_Вх·(0,056+0,56)-2646·0,056=0;

R_Вх=1323 (Н)

R_Вх2436 (Н)

m_Вх=0;

-R_Ах·(a+b)+F_t·b = 0;

R_Ах=(26460,056)/0,112=1323 (Н)

Проверка m_Кх=0;

-R_Ах +R_Вх=0

Назначаем характерные точки 1,2,2’,3 и 4 и определяем в них изгибающие моменты:

М_1х=0;

М_2х= -R_Ах·а;

М_2х=-1323·0,056=-74,08 (Н·м);

М_3х=0;

М_4х=0;

Строим эпюру изгибающих моментов М_х.

Крутящий момент

Т_I-I=0;

Т_II-II=T₁=F_t·d/2;

Т_II-II=26460,235/2=310,9 (Н·м)

Рисунок 8 - Эпюры изгибающих и крутящих моментов ведомого вала

Построим отдельную эпюру для муфты:

RAK= Fmc/(a+b); RBK= Fm(a+b+c)/(a+b); М₁=0; М₂= 0; М₃=- RAK a

RAK=3109,2(Н); RBK=905,2(Н); М₃=-174,12 (Н·м)

М₄=0.

По вычисленным данным: Mx=52,2(Н·м), My=74,08(Н·м).

Определим значение первого опасного значения:

(Н·м)

(Н·м)- 2-е опасное сечение.

2.5.4 Расчет тихоходного вала на статическую прочность

Коэффициент перегрузки: Kп=Tmax/T; Kп=2,2

Суммарный изгибающий момент Мmax= Kп·

Мmax= 2,2·90,6=199,32(Н·м)

Крутящий момент Мкmax= Kп·T2

Мкmax= 2,2·310,9=683,9 (Н·м)

Осевая сила: Fmax= Kп·Fa

Fmax= 2,2·425=935 (Н)

δj=0,95

Момент инерции при расчетах на жесткость (осевой):

( )

Момент сопротивления при расчете на изгиб:

(мм³)

Момент сопротивления при расчете на кручение:

(мм³)

Площадь сечения при расчете на растяжение(сжатие):

(мм²)

Нормальное напряжение:

(МПа)

Касательное напряжение:

(МПа)

Частные коэффициенты запаса прочности по нормальным напряжениям:

Частные коэффициенты запаса прочности по касательным напряжениям:

Общий коэффициент запаса прочности по пределу текучести:

_{Статическая прочность считают обеспеченной, если:}

_{Данное условие выполняется.}

2.5.5 Расчет тихоходного вала на сопротивление усталости

Для 1-го опасного сечения:

Коэффициент запаса по нормальным и касательным напряжениям:

_{Предел выносливости гладких образцов при симметричном цикле изгиба и кручения:}

_{Коэффициенты снижения предела выносливости:}

_{Эффективный коэффициент концентрации напряжения Kσ=1,7(при выполнении паза дисковой фрезой) и Kτ=2,05.}

_{Коэффициент влияния абсолютных размеров поперечного сечения Kdσ=0,81(изгиб для углеродистой стали) Kdτ=0,81.}

_{Коэффициент влияния качества поверхности KFσ=0,96 (Обтачивание тонкое) KFτ=0,97.}

_{Коэффициент влияния поверхностного упрочнения KV=1,0 (без упрочнения).}

_{Для первого опасного сечения вычислим коэффициент запаса прочности:}

_{S>2,5- условие выполняется.}

Для 2-го опасного сечения:

Коэффициент запаса по нормальным и касательным напряжениям:

_{Предел выносливости гладких образцов при симметричном цикле изгиба и кручения:}

_{Коэффициенты снижения предела выносливости:}

_{Эффективный коэффициент концентрации напряжения Kσ/ Kdσ =3,8(при оценке концентрации напряжений в местах установки на валу деталей) и Kτ/ Kdτ =2,3.}

_{Коэффициент влияния качества поверхности KFσ=0,96 (Обтачивание тонкое) KFτ=0,97.}

_{Коэффициент влияния поверхностного упрочнения KV=1,0 (без упрочнения).}

_{Для первого опасного сечения вычислим коэффициент запаса прочности:}

_{S>2,5- условие выполняется.}

2.5.6 Определение диаметров быстроходного вала

где [τ_к]=(20…40) (Мпа)

Принимаем [τ_к]=30 (Мпа).

; - принятое значение

Согласовываем d₁с диаметром цепной муфты , для этого определяем расчетный момент, передаваемый муфтой:

Т_м=Т₂К, где К – коэффициент, учитывающий условия эксплуатации привода. К=1,3…1,5

Принимаем К=1,5

Т_м=63,31,5=95,35 (Н∙м).

Необходимо соблюдать условие Т_м<[T], где [T] – допускаемый момент, передаваемый муфтой

В нашем случае необходимо принять [Т] 125(Н∙м)

Тогда принимаем окончательно

d_м2=36(мм);

l_м2=39(мм). (Длина полумуфты) Тип 2, исполнение 2.

Проверяем возможность соединения валов стандартной муфтой

;

; (мм).

Так как соединение валов стандартной муфтой возможно.

d₂ = d₁ + 2×t – диаметр вала под утопление крышки с отверстием и подшипник

_{d2=22+2·3.5=29(мм)}

_{d2=30(мм)-принятое значение}

_l2 » 1.25×d₂ - длина вала под утопление крышки с отверстием и подшипник

_{l2= 37.5(мм)}

d₃ = d₂ + 3.2×r

_{d3=30+3∙2=36(мм)- диаметр вала под шестерню}

_{d3=36(мм)-принятое значение}

d₄ = d_{2 -} диаметр вала под подшипник

d₄ =30(мм)

l₄=B - для шариковых подшипников, где B-ширины подшипников опор

Намечаем приближенную конструкцию быстроходного вала редуктора (рис.9).

Рис.9 Приближенная конструкция ведущего вала

2.5.7 Определение возможности изготовления вала-шестерни

Определяем размер х (рис.10)

Рис.10 Схема для определения размера х

По ГОСТ23360-78 для диаметра 36мм предварительно выбираем шпонку сечением bh=108мм. Подставив в формулу (5.1) значения получим

;

так как размер получился отрицательный, значит изготовление вала и шестерни отдельно невозможно.

2.5.8 Эскизная компоновка вала-шестерни

Назначаем предварительно подшипники шариковые радиальные однорядные легкой серии по (мм) подшипник №206.

Подшипник 206 ГОСТ 8338-75

Размеры: d=30(мм), D=72(мм), B=16(мм), r=1,5(мм)

Грузоподъемность: С_{r=19.5(кН),} С_{r0=10,0(кН)}

Выполняем эскизную компоновку вала редуктора. Необходимо определить длину вала L и расстояния от середины подшипников до точек приложения нагрузок a, b и с (рис.11).

l=(0,8…1)d_а – расстояние между серединами подшипников;

l=(0,8…1)52,6; принимаем l=52(мм);

а=b=l;

а=b=52 (мм);

с= В/2+ l1+50=16/2+26,4+50=85 (мм)

L=В/2+a+b+c=16/2+52+52+85=197 (мм);

L= 200 (мм) – принятое значение

Рис.11 Эскизная компоновка вала-шестерни

2.5.9 Расчет вала-шестерни на изгиб с кручением

Определим реакции в подшипниках в вертикальной плоскости (ось у)

m_Ау=0

-R_By·(a+b)+F_r·a- Fad/2=0

R_By=(F_r·а- Fad/2)/ (a+b);

R_By= (975·0,052-425·0,048/2)/ 0,104=389,4(Н)

Принимаем R_By=389(Н)

m_Ву=0

R_Аy·(a+b)-F_r·b- Fad/2=0

R_Аy=(F_r·b+ Fad/2)/ (a+b);

R_Аy =(975·0,052+425·0,048/2)/ 0,104 =585,57(Н)

Принимаем R_Аy=586(Н)

Проверка: F_Ку=0

R_Аy- F_r+ R_By=586-975+389=0

Назначаем характерные точки 1,2,2’,3 и 4 и определяем в них изгибающие моменты:

М_1у=0;

М_2у= R_Аy·а;

М_2у=586·0,052=30,47 (Н·м);

М_2’у= М_2у- Fad/2 (слева);

М_2’у=30,47 -10,2 =20,27 (Н·м);

М_3у=0;

М_4у=0;

Рисунок 12 - Эпюры изгибающих и крутящих моментов ведущего вала

Строим эпюру изгибающих моментов М_у, (Н·м) (рис.12)

Рассматриваем горизонтальную плоскость (ось х)

m_Ах=0;

R_Вх·(a+b)- F_t·a=0;

R_Вх·(0,052+0,052)-2646·0,052=0;

R_Вх=1323 (Н)

m_Вх=0;

-R_Ах·(a+b)+F_t·b = 0;

R_Ах=26460,052/0,104=1323 (Н)

Проверка: m_Кх=0;

-R_Ах +R_Вх=-1323+1323=0

Назначаем характерные точки 1,2,2’,3 и 4 и определяем в них изгибающие моменты:

М_1х=0;

М_2х= -R_Ах·а;

М_2х=-1323·0,052=-68,79(Н·м)

М_3х=0

М_4х=0

Строим эпюру изгибающих моментов М_х.

Крутящий момент

Т_I-I=0;

Т_II-II=T₁=F_t·d/2; Т_II-II=26460,048/2=63,5(Н·м)

Построим отдельную эпюру для муфты:

где Т₁ – вращающий момент на тихоходном валу, Н∙м

RAK= Fmc/(a+b); RBK= Fm(a+b+c)/(a+b); RAK= 1815(Н) RBK=816 (Н)

М₁=0; М₂= 0; М₃=- RAK a

М₃=-84,99 (Н·м)

М₄=0.

По вычисленным данным: Mx=30,47 (Н·м), My=68,79 (Н·м).

Определим значение первого опасного значения:

(Н·м)

(Н·м)- 2-е опасное сечение.

2.5.10 Расчет быстроходного вала на статическую прочность

Коэффициент перегрузки: Kп=Tmax/T; Kп=2,2

Суммарный изгибающий момент Мmax= Kп·

Мmax= 2,2·75,2=165,44(Н·м)

Крутящий момент Мкmax= Kп·T1

Мкmax= 2,2·63,99=140,778 (Н·м)

Осевая сила: Fmax= Kп·Fa

Fmax= 2,2·425=935 (Н)

Момент сопротивления при расчете на изгиб:

(мм³)

Момент сопротивления при расчете на кручение:

(мм³)

Площадь сечения при расчете на растяжение(сжатие):

(мм²)

Нормальное напряжение:

(МПа)

Касательное напряжение:

(МПа)

Частные коэффициенты запаса прочности по нормальным напряжениям:

Частные коэффициенты запаса прочности по касательным напряжениям:

Общий коэффициент запаса прочности по пределу текучести:

_{Статическая прочность считают обеспеченной, если:}

_{Данное условие выполняется.}

2.5.11 Расчет быстроходного вала на сопротивление усталости

Для 1-го опасного сечения:

Коэффициент запаса по нормальным и касательным напряжениям:

_{Предел выносливости гладких образцов при симметричном цикле изгиба и кручения:}

_{Коэффициенты снижения предела выносливости:}

_{Эффективный коэффициент концентрации напряжения Kσ=1,7(при выполнении паза дисковой фрезой) и Kτ=2,05.}

_{Коэффициент влияния абсолютных размеров поперечного сечения Kdσ=0,81(изгиб для углеродистой стали) Kdτ=0,81.}

_{Коэффициент влияния качества поверхности KFσ=0,96 (Обтачивание тонкое) KFτ=0,97.}

_{Коэффициент влияния поверхностного упрочнения KV=1,0 (без упрочнения).}

_{Для первого опасного сечения вычислим коэффициент запаса прочности:}

_{S>2,5- условие выполняется.}

Для 2-го опасного сечения:

Коэффициент запаса по нормальным и касательным напряжениям:

_{Предел выносливости гладких образцов при симметричном цикле изгиба и кручения:}

_{Коэффициенты снижения предела выносливости:}

_{Эффективный коэффициент концентрации напряжения Kσ/ Kdσ =3,8(при оценке концентрации напряжений в местах установки на валу деталей) и Kτ/ Kdτ =2,3.}

_{Коэффициент влияния качества поверхности KFσ=0,96 (Обтачивание тонкое) KFτ=0,97.}

_{Коэффициент влияния поверхностного упрочнения KV=1,0 (без упрочнения).}

_{Для первого опасного сечения вычислим коэффициент запаса прочности:}

_{S>2,5- условие выполняется.}

2.6 Проектный и проверочный расчет соединения колеса с валом

2.6.1 Подбор и проверочный расчет шпонки быстроходного вала

Рис.13 Сечение вала по шпонке

Для выходного конца быстроходного вала при d=34 мм подбираем призматическую шпонку bxh=10x8 мм² при t=5мм (рис.13).

При длине ступицы муфты l_М=39 мм выбираем длину шпонки l=22мм.

М атериал шпонки – сталь 45 нормализованная. Напряжения смятия и условия прочности определяем по формуле:

где Т – передаваемый момент, Нмм; Т_II=63,99Н

l_р – рабочая длина шпонки, при скругленных концах l_р=l-b,мм;

[]_см – допускаемое напряжение смятия.

С учетом того, что на выходном конце быстроходного вала устанавливается полумуфта из ст.3 ([]_см=110…190 МПа) вычисляем:

У словие выполняется.

2.6.2 Подбор и проверочный расчет шпонок тихоходного вала

Для выходного конца тихоходного вала при d=22 мм подбираем призматическую шпонку bxh=8x7мм² при t=4мм. Т_II=310,9 (Н·м)

При длине ступицы муфты l_М=82 мм выбираем длину шпонки l=70мм.

С учетом того, что на выходном конце быстроходного вала устанавливается полумуфта ([]_см=110…190 МПа) вычисляем:

Условие выполняется.

Для соединения тихоходного вала со ступицей зубчатого колеса при d=50 мм подбираем призматическую шпонку bxh=16x10 мм² при t=6 мм. При l_ст=70 мм выбираем длину шпонки l=45мм.

Материал шпонки – сталь 45 нормализованная.

У словие выполняется.

Выбранные данные сведены в табл.3.

Таблица 3

Параметры шпонок и шпоночных соединений

Параметр	Вал-шестерня - полумуфта	Вал-полумуфта	Вал-колесо
Ширина шпонки b,мм	10	8	16
Высота шпонки h,мм	8	7	10
Длина шпонки l,мм	22	70	45
Глубина паза на валу t,мм	5	4	6
Глубина паза во втулке t1,мм	3,3	3,3	4,3

2.7 Расчет подшипников

2.7.1 Подбор подшипников тихоходного вала

Исходные данные: n₂=n_II=63,3 мин^-1; d_п2=42мм; R_Аy=933Н; R_Ах=1323Н; R_By=42 Н;R_Вх=1323 Н; Н, Y = 0 – коэффициент осевой нагрузки выбранного подшипника; X = 1 – коэффициент радиальной нагрузки выбранного подшипника.

Определяем радиальные нагрузки, действующие на подшипники

;

;

Здесь подшипник 2 – это опора А в сторону которой действует осевая сила F_а (см. рис.8).

;

;

Назначаем тип подшипника, определив отношение осевой силы к радиальной силе того подшипника, который ее воспринимает (здесь подшипник 2)

; ;

Так как соотношение меньше 0,35, то назначаем шариковый радиальный однорядный подшипник легкой серии по d_п2=45мм .

Подшипник 209 ГОСТ 8338-75

Размеры: d=45(мм), D=85(мм), B=19(мм), r=2(мм)

Грузоподъемность: С_{r=33.2(кН),} С_{r0=18.6(кН)}

Определяем коэффициент осевого нагружения по отношению .

; ; е=0,197

Проверяем выполнение неравенства

;

где V – коэффициент вращения, при вращении внутреннего кольца V=1.

.

Определяем номинальную долговечность подшипников в часах

F_э=VF_r2K_K_τ;

где K_ - коэффициент безопасности;

K_ =1,3…1,5

принимаем K_ =1,5;

K_τ – температурный коэффициент;

K_τ =1 (до 100ºС)

F_э=147281,51; F_э=7092Н=7,092кН.

Подставляем в формулу :

; ч.

По результатам расчеты подшипники на обеих опорах выдерживают нагрузки.

2.7.2 Подбор подшипников быстроходного вала

Исходные данные: n₂=n_II=316,52 мин^-1; d_п2=30мм; R_Аy=586Н; R_Ах=1323Н; R_By=389 Н;R_Вх=1323 Н; Н; Y = 0 – коэффициент осевой нагрузки выбранного подшипника; X = 1 – коэффициент радиальной нагрузки выбранного подшипника.

Определяем радиальные нагрузки, действующие на подшипники

;

;

Здесь подшипник 2 – это опора А в сторону которой действует осевая сила F_а (см. рис.12).

;

;

Назначаем тип подшипника, определив отношение осевой силы к радиальной силе того подшипника, который ее воспринимает (здесь подшипник 2)

; ;

Так как соотношение меньше 0,35, то назначаем шариковый радиальный однорядный подшипник легкой серии по d_п2=30мм .

Подшипник 206 ГОСТ 8338-75

Размеры: d=30(мм), D=62(мм), B=16(мм), r=1,5(мм)

Грузоподъемность: С_{r=19.5(кН),} С_{r0=10,0(кН)}

Определяем коэффициент осевого нагружения по отношению .

; ; е=0,197

Проверяем выполнение неравенства

;

где V – коэффициент вращения, при вращении внутреннего кольца V=1.

.

Определяем номинальную долговечность подшипников в часах

F_э=VF_r2K_K_τ;

где K_ - коэффициент безопасности;

K_ =1,3…1,5

принимаем K_ =1,5;

K_τ – температурный коэффициент;

K_τ =1 (до 100ºС)

F_э=132621,51; F_э=4893Н=4,893кН.

Подставляем в формулу :

; ч.

По результатам расчеты подшипники на обеих опорах выдерживают нагрузки.

3 РАСЧЕТ КЛИНОРЕМЕННОЙ ПЕРЕДАЧИ

Для передачи крутящего момента от электродвигателя к редуктору в проектируемом приводе используется клиноремённая передача.

Выберем диаметр ведущего шкива:

Принимаем диаметр шкива равным D₁ = 140 (мм).

Рассчитаем скорость ремня: υ = π D₁ n_дв /60∙10³

υ = π∙140∙636,9/(60∙10³) = 4,67 (м/с)

По мощности двигателя Р_дв = 2,23 (кВт) и n_дв = 636,9 (об/мин) выбираем стандартный тип ремня: тип Б.

Рассчитываем диаметр ведомого шкива: D₂ = D₁∙ U_рем (1-ξ); ξ-коэффициент проскальзывания ремня.

D₂ = 140∙2,24 (1-0,01) = 315 (мм)

Выбираем ближайшее значение из нормального ряда чисел: D₂ = 320 (мм)

Рассчитываем фактическое передаточное число ременной передачи: U_факт = D₂ / D₁(1-ξ)

U_факт = 315/140(1-0,01) = 2,24.

Рассчитываем максимальную величину межосевого расстояния: а=D₁+D₂ = 140+315 = 455 мм.

Длина ремня: L_р = 2 а + π (D₁+D₂ )/2 + (D₂- D₁)²/4 а

L_р = 2∙455 + π/2∙(140+315) + (315-140) ²/4·455 = 1641,18 (мм)

Выбираем ближайшее из стандартного ряда по ГОСТ 1284.1-80: L_р = 1600 мм

Тогда уточняем межосевое расстояние по стандартной длине:

а = (2L - π (D₁+D₂ ) + [(2L - π (D₁+D₂ ))² – 8(D₂- D₁)²]^1/2)/8

а = (2∙ 1600 – 3,14(140+315) + [(2∙1600 – 3,14 (140+315))² – 8(315-140)²]^1/2)/8 = 434 (мм)

Определяем угол обхвата ремня: α = 180 – (D₁-D₂) ∙ 57°/a

α = 180 – 175∙ 57°/434 ≈ 157°. Значит, коэффициент угла обхвата, соответствующий углу обхвата равному 157° Сα = 0,93

Коэффициент, учитывающий длину ремня: L_р/ L₀ = 1600/2240 = 0,71 C_L = 0,85

Коэффициент режима работы при двусменном режиме работы: С_реж = 1,2

Мощность, передаваемая при стандартных условиях ремнем Б, длиной L₀ = 2240 мм P₀ = 2,90 кВт.

Допустимая нагрузка на ремень: Р_допуст = Р₀ Сα С_L/ С_реж

Р_допуст = 2,90∙ 0,92∙0,85/1,2 = 1,89 кВт

Определение числа ремней: Z = Р_дв/Р_допуск С_z, где С_z = 0,9

Z = 2,23/2,3 ∙0,9 = 1,06. Берем Z = 1

Предварительное натяжение ветвей клинового ремня

Н

где  – коэффициент, учитывающий центробежную силу, =0,18 Н·с²/м².

Усилие, действующее со стороны ременной передачи на валы

F_в = 2·F₀·z·sin(₁/2) = 2·476·2·sin(157/2) = 1153 Н.

где: Р_дв = 2,23 кВт; С_реж = 1,2; α_рем = 157˚; υ_ремня =4,67 м/с; С_α = 0,92; С_z = 0,9

Ширина обода шкива находится по формуле:

B_ш= (z–1)·e + 2f = (2–1)·2 + 2·12,5 = 27 (мм), где e=2 мм, f=12,5 – размеры канавок.

Рабочий ресурс передачи: , где =4,7* - базовое число циклов.

При среднем режиме работы рабочий ресурс ремня не должен быть меньше 2000 ч. Данное условие выполняется.

4. ПОДБОР И ПРОВЕРОЧНЫЙ РАСЧЕТ МУФТЫ

4.1 Подбор муфты для быстроходного вала

Подбор муфты осуществляется по техническому заданию, проектному расчету валов и энерго-кинематическому расчету:

Т_расч. = K*Т₁ – расчетный крутящий момент для подбора муфты,

где K – коэффициент режима работы, K = 1.5 – для работы с переменными колебаниями.

Т_расч. = 1.5*63.3 = 95.35 (Н*м).

Выбрана муфта со следующими параметрами:

d = 36 (мм) – диаметр внутреннего отверстия полумуфты на валу шестерне,

D=125 (мм)-наружный диаметр муфты

Коэффициент трения f= 0,3; [ρ]<0,25 МПа

Диаметр кольца трения: наружный D1=(3,5-4)*d=126-144, принимаем 130 (мм).

Внутренний D2=2,5*d=90 (мм).

Приведенный радиус кольца трения (мм)

Допускаемая осевая сила [Fa]=[ρ] /4=1727 (Н).

Число пар трения z=3,3 Округляем до четного числа z=4

Уточняем: Fa=Tp/fzR; Fa=1429 (Н)

Условие Fa<[Fa] выполнено.

4.2 Подбор муфты для тихоходного вала

Подбор муфты осуществляется по техническому заданию, проектному расчету валов и энерго-кинематическому расчету:

Т_расч. = K*Т₂ – расчетный крутящий момент для подбора муфты, где K – коэффициент режима работы, K = 1.5 – для работы с переменными колебаниями.

Т_расч. = 1.5*310.9 = 466,35 (Н*м).

Выбрана муфта со следующими параметрами:

d = 40 (мм) – диаметр внутреннего отверстия полумуфты на валу,

D=200 (мм)-наружный диаметр муфты

Коэффициент трения f= 0,3; [ρ]<0,25 МПа

Диаметр кольца трения: наружный D1=(3,5-4)*d=140-160, принимаем 150 (мм).

Внутренний D2=2,5*d=100 (мм).

Приведенный радиус кольца трения (мм)

Допускаемая осевая сила [Fa]=[ρ] /4=2453 (Н).

Число пар трения z=10,01 Округляем до четного числа z=10

Уточняем: Fa=Tp/fzR; Fa=2451 (Н)

Условие Fa<[Fa] выполнено.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Анурьев В.И. Справочник конструктора-машиностроителя. Изд. 8-е в 3-х тт. – М.: Машиностроение, 1999.

2. Дунаев П.Ф., Леликов О.П. Конструирование узлов деталей машин: Учеб. Пособие для техн. спец. Вузов.– 7-е издание., испр.– М.: Высш. шк., 2001. – 447 с.: ил.

3. Баласанян Р.А. Атлас деталей машин. Учебник для техн. вузов. – Х.: Основа, 1996. – 256 с.