0057 / Dmitrieva_Detali_mashin_i_osnovy_konstruirovania_Kratkiy_kurs_Primery_raschetov
.pdf
ПРОЧНОСТНОЙ РАСЧЕТ ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ 61
Коэффициент, учитывающий влияние характера приложения нагрузки: при одностороннем приложении нагрузки YA = 1; при двухстороннем – YA = 1 – γA, где γA = 0,35 для сталей твердостью HB ≤ 350; γA = 0,25 при HB > 350 (HRCэ > 45).
Коэффициент запаса при изгибе SF принимают по табл. 8.1. Коэффициент долговечности
4 106
YN = qF 
≥ 1. (8.52)
NFE
Его максимальные значения: YN ≤ 4 при qF = 6; YN ≤ 2,5 при qF = 9. При этом показатель степени qF для колес с однородной структурой материала, включая закаленные при нагреве ТВЧ и со сквозной закалкой, а также зубчатых колес со шлифованной переходной поверхностью, независимо от твердости и термообработки их зубьев, qF = 6. Для зубчатых колес с поверхностным упрочнением и нешлифованной переходной поверхностью qF = 9.
Если NFE ≥ NFG = 4·106, то YN = 1.
Эквивалентное число циклов при изгибе за срок службы
|
|
NFE = NΣµF. |
|
|
|
(8.53) |
|||||||
Здесь коэффициенты режима работы определяют по формуле |
|||||||||||||
|
|
|
|
∑niti (Ti |
/ Tmax ) qF |
|
|||||||
µF = µ6(9) = |
|
|
|
∑niti |
|
, |
(8.54а) |
||||||
|
|
|
|
|
|
|
|
|
|
||||
при ni = const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
i |
|
T |
qF |
|
|
|
µ |
|
= µ |
|
= |
∑ |
|
|
|
i |
|
|
(8.54б) |
|
F |
6(9) |
|
|
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
tΣ Tmax |
|
|
|||||
а суммарные числа циклов нагружения за период службы для шестерни NΣ1 и колеса NΣ2 определяются по формулам (8.6) или (8.6а) и (8.6б).
Коэффициент, учитывающий градиент напряжений:
Yδ = 1,082 – 0,172lgm. |
(8.55) |
Коэффициент YR, учитывающий шероховатость переходной поверхности, назначают: при шлифовании и зубофрезеровании с
62 Глава 8. ЗУБЧАТЫЕ ПЕРЕДАЧИ С ЦИЛИНДРИЧЕСКИМИ КОЛЕСАМИ
шероховатостью не более Ra = 40 мкм YR = 1. Для полированных колес: цементованных, нитроцементованных, азотированных и при закалке ТВЧ по контуру с охватом впадины – YR = 1,05; улучшенных, нормализованных и при сквозной закалке ТВЧ – YR = 1,2.
Коэффициент, учитывающий размеры зубчатого колеса:
YX = 1,05 – 0,000125dw. |
(8.56) |
Расчет на изгибную прочность при действии максимальной нагрузки
16. Напряжения изгиба при действии максимальной нагрузки определяют по формуле
σF |
= σF |
KAS |
≤ [σ]F |
, |
(8.57) |
|
K |
|
|||||
1max |
1 |
A |
1max |
|
||
|
|
|
|
|
|
|
где σF – находят по формуле (8.45), коэффициент KA принимают по табл. 8.6.
Коэффициент внешней динамической нагрузки KAS при расчетах на прочность по максимальной нагрузке принимают
по табл. 8.9.
17. Допускаемые напряжения изгиба при максимальной нагрузке определяют по формуле
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
[σ] |
F1max |
= |
σFSt |
Y |
gSt |
Y |
Y |
X |
, |
(8.58) |
|
|
|
||||||||||
|
|
|
|
SFSt |
dSt |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
где |
0 |
– базовое предельное напряжение при изгибе максималь- |
||||||||||
σFSt |
||||||||||||
ной нагрузкой (табл. 8.1); SFSt = 1,75/Yz – коэффициент запаса прочности при вероятности неразрушения 0,99, Yz – коэффициент, учитывающий способ получения заготовки; YgSt – коэффициент, учитывающий влияние шлифования переходной поверхности зуба: для шлифованных колес сквозной закалки с нагревом ТВЧ – YgSt =
=1,1; цементованных – YgSt =1,05; нитроцементованных – YgSt =
=0,95; при отсутствии шлифования – YgSt = 1; YdSt – коэффициент, учитывающий влияние деформационного упрочнения: при нешлифованной переходной поверхности зуба – YdSt = 0,95; при шлифованной поверхности и отсутствии деформационного упрочнения – YdSt = 1; YX определяют по формуле (8.56).
ПРОЧНОСТНОЙ РАСЧЕТ ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ 63
8.9. Значения коэффициента KAS
Вид рабочих машин и условия их эксплуатации |
KAS |
|
Приводы с асинхронными электродвигателями при |
2,5…5,0 |
|
пуске |
|
|
|
|
|
Главные приводы металлорежущих станков с элек- |
1,5…4,0 |
|
тродвигателями |
|
|
|
|
|
Лебедки, строгальные и долбежные станки, скреб- |
1,5…2,5 |
|
ковые транспортеры, фрикционные прессы |
|
|
|
|
|
Грузоподъемные машины: |
|
|
механизмы подъема |
1,2…2,0 |
|
механизмы передвижения |
1,5…4,0 |
|
|
|
|
Вентиляторы, воздуходувки |
1,4…1,8 |
|
|
|
|
Электрический транспорт |
1,6…2,5 |
|
|
|
|
Мельницы, глиномялки, смесители |
1,8…2,2 |
|
|
|
|
Камнедробилки |
2,0…3,5 |
|
|
|
|
Кривошипно-ползунные и эксцентриковые меха- |
1,8…3,0 |
|
низмы |
|
|
|
|
|
Прокатные станы |
2,5…4,5 |
|
|
|
|
Проектировочный расчет на сопротивление усталости при изгибе зуба
Расчет проводится для открытых передач, а также закрытых, при весьма ограниченном сроке службы.
Нормальный модуль находят из выражения
T2 KFβYFS1 |
|
m = Km uξ12ψbd [σ]F1 |
(8.59) |
и округляют до стандартного по табл. 8.5.
64 Глава 8. ЗУБЧАТЫЕ ПЕРЕДАЧИ С ЦИЛИНДРИЧЕСКИМИ КОЛЕСАМИ
Здесь Km = 14 – для прямозубых, Km = 12,5 – косозубых при εβ ≤ 1, Km = 11,2 при εβ > 1 для шевронных передач; T2 – наибольший момент на колесе, Н·м, длительность действия которого за срок службы больше или равна 50 000 циклов; KFβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий, определяют по рис. 8.12; z1 – число зубьев шестерни, выбирают возможно меньшим, но исключающим подрезание (целесообразно применение колес со смещением); YFS – коэффициент, учитывающий форму зубьев и концентрацию напряжений, берут по рис. 8.13; ψbd – коэффициент ширины, выбирают в зависимости от точности изготовления; [σ]F1 – допускаемое на-
пряжение изгиба для шестерни, устанавливают по формуле (8.50).
8.3. ПРИМЕР РАСЧЕТА ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ КОСОЗУБОЙ ПЕРЕДАЧИ
Исходные данные:
T1 = (TII) = 51,1 Н·м – вращающий момент на валу шестерни; T2 = (TIII) = 247,8 Н·м – вращающий момент на валу колеса; n1 = (nII) = 965 мин–1 – частота вращения вала шестерни;
n2 = (nIII) = 193 мин–1 – частота вращения вала колеса; u = (uз.п) = 5 – передаточное число зубчатой передачи.
В скобках указаны обозначения параметров, рассчитанные в подглаве 7.2 (табл. 7.1). Режим нагружения задается блоком нагружения (рис. 7.2, б).
П р и м е ч а н и е . Приняты следующие основные и дополнительные индексы для буквенных обозначений, используемых при расчете параметров: F – относящиеся к изгибной прочности; H – относящиеся к контактной прочности; 1 – относящиеся к шестерне; 2 – относящиеся к колесу.
Решение.
Проектировочный расчет по контактным напряжениям
1. Установление основных данных
В соответствии с рекомендациями по табл. 8.1 выбираем материал зубчатых колес и вид термообработки:
–шестерня – сталь 40Х со сквозной закалкой при нагреве ТВЧ до твердости 48…55 HRCЭ;
–колесо – сталь 45, улучшенная до твердости 235…265 НВ с
пределом текучести σт = 590 МПа (см. рис. 8.11).
ПРИМЕР РАСЧЕТА ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ |
65 |
||
|
|
|
|
Расчет будем вести |
по |
средней твердости: шестерни |
– |
50 HRCэ, колеса – 250 НВ2. |
|
|
|
Степень точности по контакту принимаем по табл. 8.2. |
|
||
Ожидаемая окружная скорость |
|
||
n13 T1 |
9653 51,1 |
|
|
v ≈ |
= |
=1,82 м/с. |
|
2000 |
|
2000 |
|
Принимаем восьмую степень точности зубчатых колес редуктора.
Так как твердость колеса НВ2 < 350, то коэффициент ширины ψbd = 0,9 (см. табл. 8.3).
Принимаем коэффициент внешней динамической нагрузки KA = 1, поскольку блок нагружения задан с учетом внешней динамической нагрузки (см. расчет по формуле (8.41)).
Учитывающий неравномерность распределения нагрузки по длине контактных линий коэффициент KHβ = 1,05 (согласно графи-
ку на рис. 8.1 для НВ2 ≤ 350 ψbd = 0,9 для кривой передач № 6).
2. Коэффициенты режима (согласно заданному блоку нагружения рис. 7.2, б):
|
|
|
|
|
t |
|
|
|
|
T |
3 |
|
|
|
|
|
|
|
|||||
µ |
|
= |
∑ |
|
|
|
i |
|
|
|
|
i |
|
= 0,25 + 0,25 0,73 + 0,25 0,53 + 0,25 0,33 = 0,374; |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
tΣ Tmax |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
t |
i |
|
|
T |
6 |
|
6 |
|
6 |
6 |
|
||||||||
µ6 |
= ∑ |
|
|
|
|
|
i |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
= 0,25 + 0,25 0,7 |
|
|
+ 0,25 0,5 |
|
+ 0,25 0,3 |
= 0,283; |
||||||||
|
|
|
|
tΣ Tmax |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
T |
|
9 |
|
|
9 |
|
9 |
9 |
|
||
µ9 = ∑ |
|
|
|
i |
i |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
= 0,25 + 0,25 0,7 |
|
+ 0,25 0,5 |
+ 0,25 0,3 |
= 0,26. |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
tΣ Tmax |
|
|
|
|
|
|
|
||||||||||
3. Допускаемые контактные напряжения при расчете на сопротивление усталости
Суммарные числа циклов нагружения за срок службы находим по формуле (8.6б):
NΣ1 = 60nзацп1Lh = 60·1·965·14 000 = 8,11·108;
NΣ2 = NΣ1/u = 8,11·108/5 = 1,62·108.
66 Глава 8. ЗУБЧАТЫЕ ПЕРЕДАЧИ С ЦИЛИНДРИЧЕСКИМИ КОЛЕСАМИ
Эквивалентные числа циклов нагружения за срок службы (см. формулу (8.8)):
NHE1 = NΣ1µ3 = 8,11·108·0,374 = 3,03·108;
NHE2 = NHE1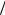 
u = 3,03·108/5 = 6,05·107.
Базовые числа циклов находим по формуле (8.5):
NHG1 = 340 HRC3,15э + 8 106 = 340 503,15 + 8 106 = 8,44 107 ;
NHG2 = 30 HB2,4 |
= 30 2502,4 = 1,71 107. |
|||||
Поскольку |
NHE1 > NHG1 , а NHE2 > NHG2 , то коэффициенты |
|||||
долговечности рассчитываем по формулам: |
||||||
ZN1 |
= 20 |
NHG1 |
= 20 |
8,44 107 |
|
= 0,938 > 0,75; |
|
|
NHE1 |
|
3,03 108 |
|
|
ZN 2 |
= 20 |
NHG2 |
= 20 |
1,71 107 |
|
= 0,939 > 0,75. |
|
|
NHE2 |
|
6,06 107 |
|
|
Если при расчете NHE1 ≤ NHG1 , а |
NHE2 ≤ NHG2 , то принима- |
|||||
ется 6-я степень корня.
Пределы контактной выносливости принимаем по табл. 8.1:
σHlim1 = 17 HRCэ + 200 = 17·50 + 200 = 1050 МПа;
σHlim2 = 2 HВ2 + 70 = 2·250 + 70 = 570 МПа.
Коэффициенты запаса:
–шестерни – SH1 = 1,1;
–колеса – SH2 = 1,1 (см. рис. 8.7).
Допускаемые напряжения шестерни и колеса находим по формуле (8.2):
[σ]H1 |
= |
σH lim1ZN1 |
ZRZv Z X |
= |
1050 0,938 |
|
0,9 = 806 МПа; |
|||
|
|
|
|
|||||||
|
|
|
SH1 |
1,1 |
|
|
||||
[σ]H 2 |
= |
σH lim 2 ZN 2 |
ZRZv Z X |
= |
570 0,939 |
0,9 = 438 МПа. |
||||
|
|
|||||||||
|
|
|
SH 2 |
1,1 |
|
|
||||
ПРИМЕР РАСЧЕТА ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ 67
Выше принято для передач общего назначения ZRZvZX = 0,9. Расчетное допускаемое напряжение находим по формулам (8.3):
[σ]H = 0,45([σ]H1 + [σ]H 2 ) = 0,45(806 + 438) = 560 МПа;
[σ]H = 1,25[σ]H lim = 1,25 438 = 548 МПа.
За расчетное напряжение принимаем меньшее, т.е. [σ]H =
=548 МПа.
4.Определение основных размеров зубчатой пары
Начальный диаметр шестерни определяем по формуле (8.9):
T2KAKHβ (u +1) |
= 675 3 |
247,8 1,0 1,05 (5 +1) |
= 41,95 мм. |
||
dw1 = 675 3 |
|
|
|
||
ψd [σ]2H |
u2 |
|
0,9 5482 |
52 |
|
Расчетную ширину колеса определяем по формуле (8.10):
bwрасч = ψbd dw1 = 0,9 41,95 = 36,7 мм.
Межосевое расстояние определяем по формуле (8.11):
расч |
|
dw1 |
(u +1) |
41,95(5 +1) |
|
|
|
aw |
= |
|
|
= |
|
= |
125,85 мм. |
|
2 |
2 |
|||||
|
|
|
|
|
|
||
Принимаем стандартное межосевое расстояние aw = 125 мм. Поскольку расчетное межосевое расстояние отличается от стандартного, уточняем ширину колеса по формуле
a |
расч |
125,85 |
|
2 |
|||
bwтреб = bwрасч |
|
w |
|
= 36,7 |
|
|
= 37 мм. |
|
|
|
|||||
|
aw |
|
|
125 |
|
|
|
|
|
|
|||||
Принимаем ширину колеса bw2 = 36 мм, ширину шестерни bw1 = bw2 + 5 = = 36 + 5 = 41 мм.
5. Определение основных параметров зубчатого зацепле-
ния
Модуль т ≈ (0,01…0,02)aw = (0,01…0,02)125 = 1,25…2,5 мм. Согласно табл. 8.5 в указанном диапазоне находятся модули: 1,25; 1,5; 1,75; 2,0; 2,25 и 2,5. Выбираем модули, соответствующие первому предпочтительному ряду: 1,5; 2,0 и 2,5. Расчет ведем для трех вариантов. Ориентировочно принимаем β = 12°. Результаты расчетов сведем в табл. 8.10.
68 Глава 8. ЗУБЧАТЫЕ ПЕРЕДАЧИ С ЦИЛИНДРИЧЕСКИМИ КОЛЕСАМИ
8.10. Основные параметры зубчатого зацепления
Параметры, формулы, размерность |
Значение параметров |
||||||||
|
|
|
|
|
|
|
|
|
|
Модуль зуба m, мм |
1,5 |
2,0 |
2,5 |
||||||
|
|
|
|
|
|
|
|||
Число зубьев шестерни с округле- |
27 |
20 |
16 |
||||||
нием до целого числа z1 = |
2aw cosβ |
|
|
|
|
||||
m(u +1) |
|
|
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
Число зубьев колеса с округлением |
135 |
100 |
80 |
||||||
до целого числа z2 = z1u |
|
|
|
||||||
|
|
|
|
|
|
|
|||
Фактическое передаточное число |
5 |
5 |
5 |
||||||
u = z2/z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Угол наклона зуба (с точностью до |
13,5905 |
16,2602 |
16,2602 |
||||||
секунд или 4-го знака после запя- |
|
|
|
||||||
той) β = arccos |
m(z1 + z2 ) |
, град. |
|
|
|
||||
|
|
|
|
|
|
||||
|
|
2aw |
|
|
|
||||
|
|
|
|
|
|
|
|||
Осевой шаг Px |
= |
πm |
, мм |
20,05 |
22,44 |
28,05 |
|||
|
|
|
|
||||||
|
|
sin β |
|
|
|
||||
|
|
|
|
|
|||||
Коэффициент |
осевого перекрытия |
1,55 |
1,38 |
1,11 |
|||||
εβ = bw2 Px |
|
|
|
|
|
|
|
|
|
П р и м е ч а н и е . Если число зубьев z < 17 (как в нашем случае при m = 2,5), то следует выполнить проверку на возможность подрезания зуба по формуле (8.15):
zmin = 2cosβ(cos2β/tg2αw + 1) = 2cos16,2602°(cos216,2602°/tg220° + 1) = = 15,28, так как zmin < 16, следовательно, при m = 2,5 происходит подрезание зуба, и этот вариант не подходит.
Передаточные числа во всех расчетных вариантах одинаковы и равны заданному, а εβ > 1, т.е. варианты примерно равнозначны. Выбираем вариант m = 1,5 мм, так как в этом случае угол β меньше углов для расчетных случаев, соответствующих m = 2 и
ПРИМЕР РАСЧЕТА ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ 69
m = 2,5, следовательно, осевая сила в зацеплении также будет меньше, а коэффициент осевого перекрытия εβ наибольший. Это значит, что передача будет работать плавней.
6. Диаметры зубчатых колес:
– делительные диаметры колес (см. формулу (8.23)):
d1 |
= |
|
mz1 |
= |
|
1,5 27 |
= 41,67 мм; |
|||
cosβ |
|
cos13,5905° |
||||||||
|
|
|
|
|
|
|||||
d2 |
= |
mz2 |
|
= |
|
1,5 135 |
|
= 208,33 мм; |
||
cosβ |
cos13,5905° |
|||||||||
|
|
|
|
|||||||
d1 + d2 = 41,67 + 208,33 = 250 = 2aw –
проверка;
– диаметры вершин зубьев (см. формулу (8.24)):
da1 = d1 + 2m(1 + x1 – y) = 41,67 + 2·1,5(1 + 0 – 0) = 44,67 мм; da2 = d2 + 2m(1 + x1 – y) = 208,33 + 2·1,5(1 + 0 – 0) = 211,33 мм.
Здесь коэффициенты смещения шестерни и колеса x1 = x2 = 0 и коэффициент воспринимаемого смещения ∆у = 0;
– диаметры впадин (см. формулу (8.25)):
d f 1 = d1 – 2m(1,25 – x1) = 41,67 – 2·1,5(1,25 – 0) = 37,92 мм;
d f 2 = d2 – 2m(1,25 – x1) = 208,33 – 2·1,5(1,25 – 0) = 204,58 мм.
Начальные диаметры совпадают с делительными, так как колеса выполнены без смещения:
dw1 = d1 = 41,67; |
|
dw2 = d2 = 208,33. |
|||||
Уточнение коэффициента относительной ширины зубчатого |
|||||||
венца проводим по формуле (8.27): |
|
||||||
ψbd = |
bw2 |
|
= |
36 |
= |
0,86. |
|
bw1 |
41,67 |
||||||
|
|
|
|
||||
70Глава 8. ЗУБЧАТЫЕ ПЕРЕДАЧИ С ЦИЛИНДРИЧЕСКИМИ КОЛЕСАМИ
7.Коэффициент торцового перекрытия рассчитывается по формуле (8.28б):
|
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
||
εα |
= 1,88 |
− 3,2 |
|
+ |
|
cosβ = |
1,88 |
− 3,2 |
|
+ |
|
|
cos13,5905° = |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
|
z2 |
|
|
|
27 |
|
135 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=1,69.
8.Суммарный коэффициент перекрытия находим по формуле (8.29):
εγ = εα + εβ = 1,69 + 1,55 = 3,24.
9. Размеры для контроля взаимного положения разноименных профилей
Постоянная хорда, выраженная в долях модуля, определяется по формуле (8.30):
sc* = π cos2 α + xsin α = π cos2 20° + 0 sin 20° = 1,3816. |
|
2 |
2 |
Постоянная хорда определяется по формуле (8.31):
*
sc = sc m = 1,3816 1,5 = 2,0728.
Высота до постоянной хорды определяется по формуле (8.32):
hc = 0,5[(da1 − d1 ) − msc*tgα]= 0,5[(43,67 − 41,67) − 1,5 1,3816tg20°] =
=1,1229.
10.Скорость и силы зацеплений
Окружная скорость определяется по формуле (8.33):
v = πdw1n1 = 3,14 41,67 965 =1,11 м/с.
60 000 |
60 000 |
Окружная сила определяется по формуле (8.34):
Ft = |
2000T2 |
2000 247,8 |
Н. |
||
|
= |
|
= 2784 |
||
|
|
||||
|
dw2 |
208,33 |
|
|
|