6633

Томский государственный университет систем управления и радиоэлектроники

Приходовский М.А.

Математика - курс лекций (семестр 1, часть 2)

для специальности:

09.03.03 «прикладная информатика в экономике»

Учебное пособие

Томск

ТУСУР

2017

1

Лекция № 8. 21. 10. 2016

Глава 5. Основы математического анализа. §1. Множества и функции.

Множеством называют совокупность объектов некоторого типа. Например, множество точек на плоскости, множество чисел, множество матриц.

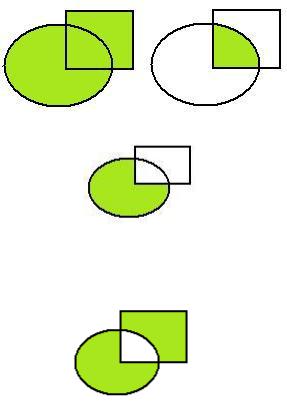
Объединение A B {x A или x B} Пересечение A B {x A и x B}

Объединение и пересечение 2 множеств показаны графически:

Разность множеств: A \ B {x A, x B}. Показано на чертеже:

Аналогично, В \ А {x В, x А}.

Объединение этих двух разностей называется симметрической разностью, и обозначается так: A B = ( A \ B) (В \ А) , на чертеже:

В то же время, это множество можно получить и другим путём: из объединения удалить пересечение. То есть,

4

( A \ B) (В \ А) = (A B) \ (В А) .

Ещё обозначения: A B - множество А является подмножеством множества В.

Числовые множества.

N {1,2,3,...}натуральные числа

Z {..., 3, 2, 1,0,1,2,3,...} целые числа

R ( , ) вся действительная ось, действительные числа. Множество R \ Q - иррациональные числа.

Верно следующее: N Z Q R .

Существует обобщение: комплексные числа вида a bi . Комплексная плоскость.

Множества на действительной оси.

Интервал (a, b) {x R a x b} - граничные точки не включены. Отрезок [a, b] {x R a x b} - здесь границы включены во

множество.

Пример. Найти объединение и пересечение множеств A (0,2) ,

Множество вида [a, ) {x R a x}. Числа «бесконечность» не

существует, поэтому в таком множестве справа всегда должна быть круглая скобка.

Интервал вида (a , a ) в будущем будем называть окрестностью радиуса точки a и обозначать U (a) .

Внутренние и граничные точки.

Если для точки a A существует окрестность, которая полностью лежит во множестве А, то есть является его подмножеством, U (a) A , то такая точка называется внутренней

точкой множества А. Если же для любой окрестности есть лишь

5

частичное пересечение со множеством А, то такая точка называется граничной точкой множества. Показано на чертеже:

Функция, аргумент, образ.

Пусть даны 2 множества X ,Y . Если задан некоторый способ каждому элементу x X поставить в соответствие какой-то y Y , то говорится, что задана ФУНКЦИЯ из X в Y . Обозначение:

f: X Y .

x называется аргументом функции, а y - образом.

Основные элементарные функции и их графики: повторить из школьного курса (!)

Степенные x a , показательные a x , логарифмические log a x , тригонометрические sin x, cosx,tgx, ctgx , обратные тригонометрические.

Лекция № 9. 28. 10. 2016

Если f : R R , то есть y f (x) , график - кривая в плоскости. Если f : R 2 R функция двух переменных, то есть z f (x, y) , её график - это поверхность в трёхмерном пространстве.

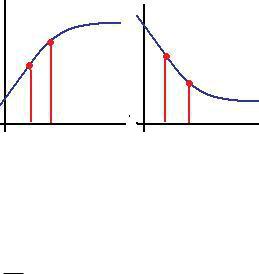
Монотонность.

Монотонно возрастающая функция: если x1 x2 то f (x1 ) f (x2 ) . Монотонно убывающая функция: если x1 x2 то f (x1 ) f (x2 ) .

6

Доказательство. Введём две функции: g(x) f (x) f (x) , 2

h(x) f (x) f (x) . Первая из них чётна, вторая нечётна. Видно, что

2

если заменить x на x , то для g(x) получится выражение, равное исходному, а вот для h(x) разность в числителе будет

Если чётную и нечётную компоненты записать для функции f (x) e x , то получатся так называемые гиперболический косинус и

Вообще, существует 3 способа задания функций - явный, неявный, параметрический.

8

Параметрический: x x(u, v), y y(u, v), z z(u, v) (в этом случае

обязательно будет два параметра). Например, 2 параметра на сфере: широта и долгота.

§2. Пределы.

Последовательность.

Множество чисел, пронумерованных с помощью натуральных чисел: {a1 , a2 , a3 ,..., an ,...} называется последовательностью. Её можно определить также и как функцию f : N R .

Графиком будет не кривая, а дискретный набор точек, потому что только над каждой точкой с абсциссой, равной натуральному числу, есть точка графика.

Арифметическая и геометрическая прогрессии тоже частный случай последовательности.

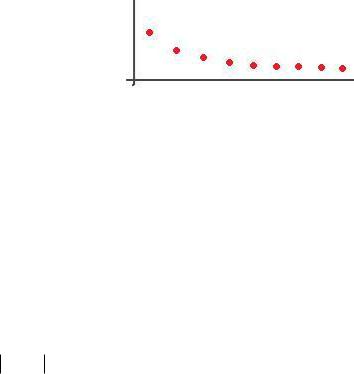
В рассмотренных примерах видно, что при возрастании номера элемент убывает к 0. Однако при этом само число 0 не достигается ни при каком номере. То есть, числа 0 в этой последовательности нет. Однако, все элементы уменьшаются и приближаются к 0. В связи с этим возникает определение предела последовательности:

Определение. Число A называется пределом последовательности {an } , если: 0 n0 N , такое, что n n0 выполняется:

A an .

(для любого числа эпсилон больше нуля, существует такой номер элемента последовательности, что для всех последующих номеров

9

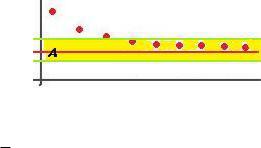
отклонение элементов от числа А меньше, чем эпсилон). В этом случае говорится, что последовательность стремится к числу А.

Обозначение предела: A lim an . (lim это от английского слова limit

n

которое хорошо известно и в русском языке - лимиты потребления света, воды и т.д. ).

Если рассмотреть полосу от A до A по высоте, то начиная с какого-то номера, все последующие точки будут попадать в эту полосу:

Чем меньше число (погрешность меньше) тем больший номер требуется .

Пример. lim 1 0 . По определению: если например требуемая

n n

точность 0,01 то n0 100 , n n0 выполняется: разность элемента и 0 менее 1/100, то есть 1/101 затем 1/102 и т.д.

* Для того, чтобы лучше понять, что такое предел, представьте следующее. Машина приближается к городу. Для любого заранее заданного расстояния (например = 10 км.) существует такой момент времени t0 , что в последующие моменты времени t t0 расстояние

будет меньше, чем . Это как раз и означает «стремится к 0», то есть расстояние уменьшается к 0. Если задать = 5 км. то это достигается в более поздний момент времени, а если = 1 км. то ещё позже.

Предел может и не существовать. Для последовательности {1,0,1,0,....},

например, предел не существует. Здесь не происходит стабилизация значений, то есть их колебания по высоте всегда 1. После каждого номера, найдётся последующий элемент, который удаляется на расстояние 1 от предыдущего, то есть эти колебания не могут быть меньше заранее заданного малого числа .

10