30
рабочего, xi |
этот разряд, fi |
wi |
частота, Si |
2 |
1 |
0,05 |
1 |
3 |
5 |
0,025 |
6 |
4 |
8 |
0,40 |
14 |
5 |
4 |
0,20 |
18 |
6 |
2 |
0,10 |
20 |
Итого |
20 |
1,00 |
|
В тех случаях, когда число вариантов дискретного признака достаточно велико, а также при анализе вариации дискретного признака, когда значения признака у отдельных единиц могут вообще не повторяться,
строятся интервальные ряды распределения.
Для определения величины интервала h для построения вариационного ряда с равными интервалами:
1.Вычисляется разность между максимальным и минимальным значениями признака первичного ряда (размах вариации, R): R = xmax − xmin ;
2.Размах вариации делится на число групп k, т.е. h = R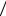
k . Число групп
приближенно |
определяется |
по |
формуле |
Стэрджесса: |
k ≈1+3,322 lg n , где n – |
общее |
число изучаемых единиц |
||
совокупности. Полученная величина округляется до целого числа.
Рассмотрим пример построения ряда распределения по первичным данным о размере прибыли 20 коммерческих банков за год (млн.руб):
xi - 3,7; 4,3; 6,7; 5,6; 5,1; 8,1; 4,6; 5,7; 6,4; 5,9; 5,2; 6,2; 6,3; 7,2; 7,9; 5,8; 4,9;
7,6; 7,0; 6,9.
Количество групп равно: k ≈1+3,322 lg 20 = 5,32 . Округляя, получаем число групп, равное 5.
Величина интервала: (8,1−3,7)
5 = 0,9 млн.руб.
В результате группировки получаем ряд распределения (табл.2).
|
|
|
Таблица 2 |
Размер прибыли, млн.руб. |
Число банков |
Накопленная частота |
|
3,7-4,6 |
(-) |
2 |
2 |
4,6-5,5 |
|
4 |
6 |
5,5-6,4 |
|
6 |
12 |
6,4-7,3 |
|
5 |
17 |
7,3-8,1 |
|
3 |
20 |
Итого |
|
20 |
|
|
31 |
|
Знак (-) в первой строке |
соответствует |
принципу |
«исключительно» и означает, что значения признака, совпадающие с верхней границей интервала, в этот интервал не включаются, а попадают в следующий интервал. Если ставится знак (+), это соответствует принципу «включительно» и означает, что значения признака, совпадающие с верхней границей интервала, включаются в эту группу.
5.2. Графическое изображение вариационного ряда
Для графического изображения дискретного ряда применяют полигон распределения. Для построения по оси абсцисс откладываются значения признака, по оси ординат – частоты или частости. Для замыкания полигона крайние вершины соединяются с точками на оси абсцисс, отстоящими на
одно деление от xmax и xmin .
На рисунке изображен полигон распределения, построенный на основе данных таблицы 1. Моде для дискретного ряда распределения соответствует значение, которому соответствует максимальная частота. В нашем примере мода равна 4.
9 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
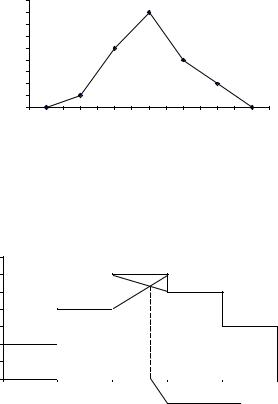
Для графического изображения интервальных вариационных рядов применяется гистограмма. Для построения по оси абсцисс откладываются равные отрезки, соответствующие величине интервалов, на которых строят прямоугольники с высотой, равной частотам или частостям интервала.
На рисунке изображена гистограмма ряда распределения банков по
7 |
|
|
|
|
6 |
|
|
|
|
5 |
|
|
|
|
4 |
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
3,7-4,6 |
4,6-5,5 |
5,5-6,4 |
6,4-7,3 Мода |
7,3-8,1 |
32
данным таблицы 2. Также показан способ графического определения моды.
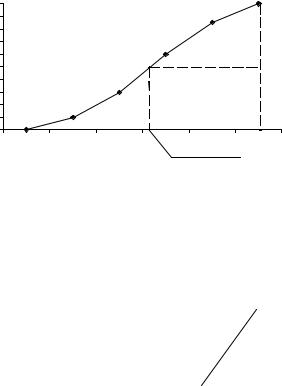
В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята) и огива. Для построения кумуляты и огивы по оси абсцисс откладывают значения признака, по оси ординат – накопленные частоты (для кумуляты) или частости (для огивы).
На рисунке изображена кумулята ряда распределения банков, построенная на основе таблицы 2 для графического определения медианы высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.
20 |
|
|
|
|
18 |
|
|
|
|
16 |
|
|
|
|
14 |
|
|
|
|
12 |
|
|
|
|
10 |
|
|
|
|
8 |
|
|
|
|
6 |
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
3,7-4,6 |
4,6-5,5 |
5,5-6,4 |
6,4-7,3 |
7,3-8,2 |
|
|
|
Медиана |
|
5.3. Показатели центра распределения
Для характеристики среднего значения признака в вариационном ряду используются средняя арифметическая, медиана и мода. Общие понятия о средних величинах были даны в главе 4. В данном параграфе рассмотрим расчет показателей центра распределения для вариационных рядов.
Средняя арифметическая:
|
k |
|
|
для дискретного ряда распределения: x |
∑xi fi |
|
|
= i=1 |
k |
, |
|
|
|
∑ fi |
|
|
|
i=1 |
|
где xi - варианты значений, |
|
|
|
fi - частота повторения |
33 |
данного варианта |
k
∑xi/ fi
для интервального ряда распределения: x = i=1
где xi/ - середина соответствующего интервала.
Для таблицы 1 средняя арифметическая равна:
x = 2 1+3 5 +4 8 +5 4 +6 2 = 4,05.
20
Для таблицы 2 средняя арифметическая равна:
k |
, |
∑ fi |
|
i=1 |
|
x = 4,15 2 +5,05 4 +5,95 6 +6,85 5 +7,75 3 = 6,085млрд.руб.
20
Медиана:
для дискретного ряда распределения положение медианы определяется ее номером NMe = (n +1)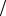
2 , где n – число единиц совокупности.
Для примера в табл.1 NMe = (20 +1)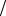
2 =10,5 , т.е. медиана равна
средней арифметической 10-го и 11-го значений признака. Ме=4.
для интервального ряда распределения сразу можно определить интервал, в котором находится медиана. Затем определяем медиану по
формуле: Me = xMe +h |
(n +1) |
2 |
−SMe−1 |
, где |
|
|
|||
|
fMe |
|||
|
|
|
||
xMe -нижняя граница медианного интервала; h – величина интервала;
SMe−1 -накопленная частота интервала, предшествующая медианному;
fMe - частота медианного интервала.
Для примера, приведенного в табл.2:
Me = 5,5 +0,9 (20 +1) 2 −6 = 6,175 млрд.руб. 6