Методы математической физики.-3

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

u xx ( x,t ) ÷ ∫ uxx ( x,t ) sinαxdx = ux ( x,t ) sinαx

∞x =0 −α ∫ ux ( x,t )cosαxdx =

= −αu( x,t )cosαx

= −αu( x,t )cosαx

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.8 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1414

Задача 3. Рассмотрим неоднородное уравнение гиперболического типа,

описывающее под действием внешней силы колебания полуограниченной струны с закрепленным концом:

utt ( x,t ) − a 2uxx ( x,t ) = f ( x,t ), x (0,∞),t (0,∞).

u( 0,t ) = 0 - граничное условие при x = 0,

u( x,0 ) = ut ( x,0 ) = 0 - начальные условия

u( x,t ) = ux	( x,t ) → 0, x → ∞,
	.
u( x,t ) ограничена при t → ∞,

Воспользуемся синус-преобразованием Фурье по координате x.

ние его ко второй производной по х и дважды дифференцирование по ют

(8.37)

(8.38)

(8.39)

Примене-

частям да-

Проинтегрированные слагаемые обращаются в ноль в силу граничных условий,

включая условия на бесконечности. Дифференцирование по t можно вынести за знак интеграла, тогда задача для трансформант сведется к следующей:

	tt ( α ,t ) + a 2α 2
u	tt ( α ,t ) + a 2α 2	u(α ,t ) = f ( α ,t ),
			(8.40)
	u( α ,0 ) = u t ( α ,0) = 0.		(8.40)
	u( α ,0 ) = u t ( α ,0) = 0.

Для ее решения применим преобразование Лапласа по t. Имеем

p 2 u(α , p ) + a 2α 2 u(α , p ) = f (α , p ),

На основании формулы (8.15) и теоремы о свертке получаем:

131

sin aα( t − τ )

u(α ,t ) = ∫

(α ,τ )

dτ .

aα

β = aα ,

( p ) =

(α , p ),

При этом было учтено, что

β 2

+ p2

( t −τ ) =

sin aα( t −τ )

, f

2 (τ ) = f

( α ,τ ).

aα

Применение формулы обращения (8.41) дает

∞ t

sin aα( t -τ )

u( x,t ) =

∫ ∫ f ( α ,τ )

dτ sinαxdα =

πa

0 0

∞

cosα [x - a( t -τ )]- cosαα [x + a( t -τ )]

∫ dτ ∫

f ( α ,τ )

dα

2πa

∞

x+a( t −τ )

∫ dτ ∫

( α ,τ )

∫ sinαzdz ×dα .

2πa

x−a( t −τ )

При проведении преобразований было учтено, что

(8.41)

sin	β1 - β 2	× sin	β1 + β 2	=	1	[cos β	2 - cos β1 ],
sin		× sin		=		[cos β	2 - cos β1 ],
2		2		2
где
			β1 + β2	= αx,
				= αx,

β1 − β2 = αa(t -τ ), 2

β1 = α[x + a(t -τ )], .

β2 = α [x - a(t -τ )]

Окончательно, формально учтя вид формулы обращения, найдем

	1	t	x+a( t −τ )
u( x,t ) =		∫ dτ	∫ f ( z ,τ )dz.
	2a
		0	x−a( t −τ )

(8.42)

132

Таким образом, решение задачи получено. Его физическую интерпретацию можно дать, задавая конкретный вид функции f(z,τ).

Задача 4. Решить краевую задачу для уравнения параболического типа,

описывающего распределение температуры вдоль теплоизолированного неогра-

ниченного стержня. Постановка задачи имеет вид

ut − a2uxx	= 0, x (− ∞,∞),t (0,∞);		(8.43)
u( x,t )		t = 0 = f ( x ),	(8.44)

ux (x, t) → 0,	u(x,t) → 0, при x → ±∞,		(8.45)
где u(x,t) – функция, описывающая распределение температуры, f(x) –			её началь-
ное распределение.

Задача в такой постановке возникает также при исследовании процесса распро-

странении тепла вдоль некоторого направления в однородной изотропной среде.

Поскольку координата x меняется в пределах от -∞ до +∞, а в бесконечно

удаленных точках задана функция и ее производная по x, то возможно исполь-

зование экспоненциального преобразования Фурье. Применение его ко второй

производной в уравнении (8.43)			после интегрирования по частям дает:
	∞						∞
uxx ( x,t ) ÷	∫ uxx ( x,t )e	iαx		dx = ux	( x,t )e	iαx	∞	( x,t )e	iαx	dx =
uxx ( x,t ) ÷	∫ uxx ( x,t )e			dx = ux	( x,t )e		x=−∞ − iα ∫ ux	( x,t )e		dx =
	−∞						−∞

= −iαu( x,t ) ∞x=−∞ eiαx − α2 u( α,t ) = −α2 u( α,t ).

Проинтегрированные члены обращаются в ноль, если учесть (8.45). Проблем с первой производной по t нет как в уравнении, так и в начальном условии. В ре-

зультате задача для трансформант приводится к виду:


ut		(α , t) + α 2 a2		u	(α , t) = 0,	(8.46)

	u( α,t )		t = 0 = f ( α ).			(8.47)

Она решается стандартным образом:

133

d u

= -α 2 a 2 dt,

= −α 2 a 2 u,

ln u(α , t)dt = −α 2a2dt,

u( , t)

u( a,t ) = Ce−α2a2t .

u( α,t )dt = −α2a2t + ln C ,

Постоянная интегрирования находится из начального условия (8.47)

и равна

C =

(α ). Тогда

( α )e−α2a2t .

u( α,t ) =

(8.47)

Восстановим оригинал:

∞

− α 2 a 2t × e−iαx da =

u( x,t ) =

∫

( a )e

2p −∞

(8.48)

∞

∫ f ( x )dx ∫ e−α 2 a 2t ×e

−iα( x −ξ )da.

−∞

Внутренний интеграл вычисляется и равен

∞

I( x,t ) = ∫ e−α2a2t × e

−iα( x−ξ )da + ∫ e−α2a2t × eiα( x−ξ )da =

∞

× cos[a( x - x )]da.

= 2∫ e−α2a2t

Рассмотрим последний интеграл

∞

− α 2 a 2t

J ( b ) = ∫ e

× cos( ba )da,

где

b = ( x - x ).

(8.49)

Вычислим его методом дифференцирования по параметру с последующим инте-

грированием по частям:

dJ ( b )

∞

−α2a2t

∞

= -∫ e

−α2a

2t × sin( ba )ada =

sin( ba )

α=∞

0 -

∫ e

−α2a2t × cos( ba )da =

2a 2t

2a 2t 0

= -

J ( b ),

ln J ( b ) = -

+ ln C.

2a 2t

4a 2t

−

β2

Окончательно имеем J ( β ) = Ce

4a2t .

134

Постоянную интегрирования C найдём из условия (8.49) при β =0, которое приводит к табличному значению интеграла Пуассона:

∞

−α a2t dα =

C = J( 0 ) = ∫ e

2 a

В результате получим

(x−ξ )2

∞

−

( x −ξ )2

−

4 a 2t

∫

I (x, t) =

t , u(x,t) =

f (ξ )e

dξ.

(8.50)

2a πt

−∞

Зная начальное

распределение f(ξ),

можно

найти

пространственно-

временное распределение температуры. При f(ξ) = const интеграл сводится к пуассоновскому. Решение полностью совпадает с (3.15), полученным методом разделения переменных.

Задача 5. Решить краевую задачу для уравнения параболического типа в полупространстве, имеющем границу x=0. Постановка задачи:

ut ( x,t ) − a2uxx ( x,t ) = 0, x (0,∞), t (0,∞), u( 0,t ) = 0,

u( x,0 ) = f ( x ),

u( x,t ), ux ( x,t ) → 0, Lпри x → ∞.

Задачу можно решить двумя способами, используя синус-преобразование Фурье и преобразование Лапласа.

1.Применив синус-преобразование Фурье, получим граничную задачу для трансформант в следующей постановке:

u( α,t )

+ a2

α2 u( α,t ) = 0,

u( α,0 ) = f ( α ).

Постановка задачи аналогична предыдущей и схема её решения подобна. С учё-

том формул, приведённых в табл. 8.1, имеем

135

= −a2α2 ,...,

( α )e− a2α2t .

u( α,t ) =

∞

− a2α2t sin αξ sin αxdα =

u( x,t ) =

∫ f ( ξ )dξ∫ e

∞∞

=1 ∫ f ( ξ )dξ∫ e− a2α2t [cos α( x − ξ ) − cos α( x + ξ )]dα =

π0 0

	1		∞		−	(x − ξ)2		−	(x + ξ)2
	1		∞		−	2		−	2
=				f ( ξ ) e		4a t	− e		4a t	dξ.
						4a t			4a t
	2a	πt ∫0
	2a	πt ∫0

Видно, что решение можно интерпретировать как прямой и обратный по-

токи тепла, идущие в противоположных направлениях от границы.

2. Применив к уравнению преобразование Лапласа по t, найдём

∞

− pt dt = ue− pt

0∞ + pu

xx = ∫ut e

= − f ( x ) + pu.

Постановка задачи для трансформанты будет иметь вид

f ( x )

u xx −

u = −

u( 0, p ) = 0.

Далее применив синус-преобразование Фурье, получим

= −

(α )

− α 2

u(α , p ) −

u(α , p ) =

a 2

+ a 2α 2

∞

(α )

∞

∞ sinαx sinαξ

u( x, p ) =

∫

sinαxdα =

∫ f ( ξ )dξ ∫

dα .

p + a 2α 2

Выполним обратное преобразование Лапласа, т.е. применим формулу об-

ращения, тогда получим

	2	∞	∞	1	σ+i∞	e	pt
u( x,t ) =		∫ f ( ξ )dξ∫ sin αx sin αξdα			∫			dp.
	π					p + a 2α2
		0	0	2πi σ−i∞

По таблице интегральных преобразований Лапласа последний интеграл равен

136

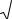
e−a2α 2t . В этом можно убедиться, выполнив преобразование Лапласа и вычислив

внутренний интеграл после замены произведения синусов по формулам тригоно-

метрии:

∞

− a2α 2t

− pt

e−( p + a2α 2 )t

∞

∫ e

× e

dt =

t =0

- ( p + a 2α 2 )

p + a 2α 2

2 ∞

∞

−

(x−ξ )2

−

(x+ξ)2

−a2α2t

4a2t

u( x,t ) =

∫ f ( x )dx∫ e

sin ax sin axda =

∫

f ( x ) e

- e

dx,

где было использовано

sin ax sin ax =

[cos( x - x )a - cos( x + x )a],

a1 + b1

= ax,

a1 - b1

= ax, т.е. a = a( x + x ),b

= a( x - x ).

Видно, что результат полностью совпадает с полученным посредством си-

нус-преобразования Фурье.

137

СПИСОК ЛИТЕРАТУРЫ

1.Емельянов В.М., Рыбакина Е.А. Уравнения математической физики. Практикум по решению задач [Электронный ресурс]: Учебное пособие. – СПб.: Лань, 2008. – 224 c. – Режим доступа: http://e.lanbook.com/books/element.php?pl1_cid=25&pl1_id=140.

2.Методы решения нелинейных уравнений математической физики и механики: Учебное пособие для вузов/ А. Д. Полянин, В. Ф. Зайцев, А. И. Жуков. –

М.: Физматлит, 2005. – 254 с.

3.Методы решения задач математической физики: Учебное пособие/ В. И. Агошков, П. Б. Дубовский, В. П. Шутяев; ред. Г. И. Марчук. – М.: Физматлит, 2002. – 320 с.

4.Князев П.Н. Интегральные преобразования: Учебное пособие для вузов. – М.: Едиториал УРСС, 2004. – 190 с.

5.Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. М.: Наука, 2003. – 688 с.

6.Гошин Г.Г., Заев Д.А. Решение краевых задач для дифференциальных уравнений в частных производных методом конечных разностей. Методические указания к компьютерной лабораторной работе. Томск: ТУСУР, 2011.–13 с.

7.Гошин Г.Г., Ларионова Е.Д. Исследование солитонов. Методические указания к компьютерной лабораторной работе. Томск: ТУСУР, 2011. – 20 с.

8.Методические указания по практическим занятиям и самостоятельной работы студентов приведены в учебно-методическом пособии [1]: глава 8 – стр.123

–133, 140 – 154.

138

Учебное издание

Гошин Геннадий Георгиевич

Методы математической физики

Учебно-методическое пособие

Для студентов, обучающихся по направлению подготовки бакалавров 210700.62

« Инфокоммуникационные технологии и системы связи»

Формат 60x84 1/16. Усл. печ. л.-----.

Тираж 30 экз. Заказ-------.

Отпечатано в Томском государственном университете систем управления и радиоэлектроники.

634050, Томск, пр. Ленина, 40. Тел. (3822) 533018.

139

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1414

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023717.66 Кб11Методы контроля и оценки качества программного обеспечения..pdf
#
05.02.20231.62 Mб10Методы манипуляции цифровой радиосвязи..pdf
#
05.02.2023865.05 Кб5Методы математического описания и расчета сложной линейной электрической цепи в стационарном режиме..pdf
#
05.02.2023589.02 Кб11Методы математической физики.-1.pdf
#
05.02.2023242.02 Кб7Методы математической физики.-2.pdf
#
05.02.20232.8 Mб11Методы математической физики.-3.pdf
#
05.02.20231.1 Mб20Методы математической физики..pdf
#
05.02.20231.66 Mб6Методы моделирования и оптимизации телекоммуникационных систем и сетей.-1.pdf
#
05.02.2023915.36 Кб7Методы моделирования и оптимизации телекоммуникационных систем и сетей..pdf
#
05.02.2023478.47 Кб7Методы неразрушающего контроля и диагностики..pdf
#
05.02.2023903.1 Кб9Методы оптимального управления в автоматизированных системах управления воздушным движением (АС УВД)..pdf