
Методы и теория оптимизации.-1
.pdf
Занятие 6. ЧИСЛЕННЫЕ МЕТОДЫ ПОИСКА УСЛОВНОГО ЭКСТРЕМУМА
Метод наискорейшего спуска. Рассмотрим grad целевой функции.
Движение по направлению вектора под острым углом будет приводить к уменьшению целевой функции, а движение против направления функции к увеличению целевой функции. Разумно за направление движения принять сам вектор – grad f.
x2
S
gradf
gradf |
x1 |
Для выбора расстояния нужно применить метод одномерной оптимизации. Прекратить поиск, когда величина grad f станет достаточно малой. Этот метод гарантирует, что найдена либо точка локального минимума, либо седловая точка.
Анализ метода.
Линии постояных значений целевой функции
Ло
гический
Век тор антигра-
Рассмотрим целевую функцию, которая является квадратичной функцией, точка локального минимума совпадает с точкой начала координат.
Пусть мы выбрали начальное приближение.
Отыскивая наименьшее значение по направлению траектории (наименьшее значение там где происходит касание grad f линии уровня).
В случае когда масштаб выбирается следующим образом (линии уровня вытя-
нуты).
21

x1
Траектория
x0
Если линии уровня Z x2 |
x2 |
- окружности, то приходим сразу в точку ло- |
1 |
2 |
|
кального минимума.
|
|
|
|
|
|
Метод Ньютона. |
|
|
1. |
f x const |
одночлен - один постоянный член любой точки данной функции |
||||||
|
является оптимальным – тривиальный случай; |
|
||||||
2. |
линейная функция (двучлен) |
f x C1 x1 |
C2 x2 |
Cn xn C0 C, x C0 |
||||
|
gardf |
|
|
f C (возможно бесконечное уменьшение и увеличение) |
||||
|
1 и 2 не подходят для оптимизации. |
|
|
|||||
3. |
трехчлен f x |
C1 x1 |
C2 x2 |
Cn xn |
C0 |
Sij xi x j |
||
|
|
|
|
|
|
|
i |
j |
|
f x |
|
1 |
Qx, x C, x C0 ; |
|
|
||
|
2 |
|
|
|||||
|
|
|
|
|
|
|
||
|
Qx, x |
|
|
y j x j |
|
qij xi xy |
|
|
|
|
|
|
j |
i |
j |
|
|
|
без ограничения общности можно положить что матрица q – симмет- |
|||||||
|
ричная qij |
q ji |
|
|
|
|
|
|
Разложим функцию в ряд Тейлора (должно быть 3 члена). Чтобы найти линейный член квадратичной функции, надо взять grad.
|
|
qij xi x j |
|
qij |
|
xi x j |
qij |
|
xi |
|
x j |
qкi xi |
хк i |
|
|
|
|
||||||||
j |
|
i j |
xк |
i j |
xк |
xк |
i |
|||||
qкj x j |
qкj x j |
|
q jк x j |
2 qкj x j |
2Qx |
|
|
|
|
|
||
j |
j |
j |
|
j |
|
|
|
|
|
|
||
22
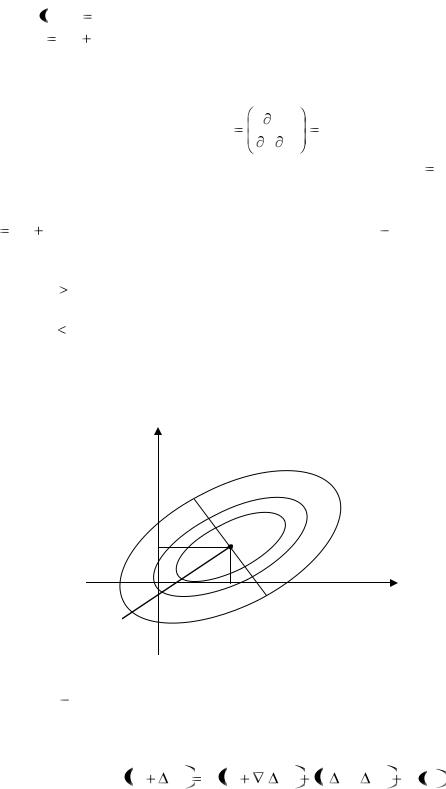
grad Qx, x 2Qx ; gradf Qx C ; С = 0
2Qx ; gradf Qx C ; С = 0
Найдем матрицу Гесса (матрица вторых частных производных)
2 |
f |
|
|
|
|
H |
|
|
|
Q |
|
|
|
|
|
||
|
xi |
x j |
|
||
элемент матрицы Гесса является элементом функции Q. hij |
qij (все частные |
||||
производные высших порядков равны 0). |
|
|
|
|
|
Функция экстремальна, если |
|
grad в данной |
точке равен 0, |
||
gradf Qx C следовательно условие экстремальности Qx  C - система.
C - система.
Необходимое условие оптимальности:
Если Q 0 решение данной системы существует и оно единственное (совместная система).
Если Q 0 решение данной системы существует и оно единственное, т.е. если
Q знакоопределена, то существует решение и оно единственное.
Если имеем квадратичную функцию и матрица положительно определена, то линии уровня – эллипсы.
Собственные значения определяют оси эллипсов.
x2
x2*
x* |
x |
1 |
1 |
Чтобы определить координаты точки локального минимума, нужно решить систему Qx2  C .
C .
Пусть f(x) – произвольная функция и надо найти точку локального минимума. Разложим функцию в ряд Тейлора в окрестности точки.
f xк |
хк |
f хк |
f хк |
Н хк , хк О |
Пусть функция не квадратичная, эллипсы примерно отражают кривизну линий |
||||
уровня и находятся в окрестности точки |
х к . В окрестности точки х к находим при- |
|||
ближение и заменяем эту функцию квадратичной функцией, которая получается из разложения в ряд Тейлора. Далее решаем задачу минимизации.
Находим точку минимума и рассматриваем эту точку как следующее приближение и т.д.
23

Для нахождения точки минимума квадратичной функции (зависит от х )необ-
ходимо решить систему: |
|
|
|
Н хк |
f |
хк |
|
Окончательно следующее приближение х к 1 |
х к |
х к . |
|
хк 1 хк Н 1 f хк |
- формула Ньютона |
||
(обобщение формулы минимизации одной переменной) |
|||
Выполнение метода останавливается когда |
|
0 , т.е. когда х к очень мало. |
|
Для получения практической точности достаточно выполнить 4 итерации метода Ньютона.
Если f – хороша, то метод Ньютона подходит, если f – квадратичная функция,
то метод Ньютона приводит к минимальной точке за 1 шаг, из любой точки. |
|
Недостатки: |
|
1. на каждом шаге итерации надо находить решение системы Н хк |
f хк ; |
2.С ростом числа итераций Н – разрежается, т.е. большое число членов становится равными 0.
Все формулы безусловной минимизации можно записать в общую схему:
1.выбор направления;
2.выбор шага.
|
|
|
|
х к - приближение в точке локально- |
|
|
|
|
го минимума, чтобы приблизиться к иско- |
|
L |
S |
мой точке х к . Мы должны выбрать направ- |
|
x* |
|
ление, в конце получим локальную линию. |
||
|
|
|
xK |
|
|
|
||||||
Допустим, |
требуется f(x)min; x0 - начальное приближение; |
xK - текущее при- |
||||||||||
ближение |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x K 1 |
x* |
|
|||
|
|
|
|
|
|
|
K |
|
|
|
||
|
|
|
n |
|
|
|
||||||
|
|
|
x K |
|
|
|
||||||
|
|
|
|
|
|
|
S K |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
а) выбор направления (gradf,n) 0 ; |
|
|
|
|||||||||
|
|
|
|
|
|
|||||||
б) движение вдоль выбранного направления X K 1 |
X K |
S K * nK |
||||||||||
24

Задачи оптимизации с ограничениями – разностями (ЗОР)
Пример:
f (x1 , x2 , x3, x4 ) min
g1 (x1 , x2 , x3, x4 ) 0
gm (x1 , x2 , x3, x4 ) 0
f (x2 , x3, x4 )
g(x2 , x3, x4 ) 0
f ( x 1 , x2 ,....,xn ) |
min |
|
|
g 1 ( x 1 , x2 ,....,xn ) |
0 |
f (x) |
min |
........................... |
.. |
g(x) |
0 |
g m ( x 1 , x2 ,....,xn ) |
0 |
|
|
Функции заданы аналитическим выражением |
q1 |
||
можно разрешить |
относительно одной из |
переменных |
|
x1 h1 (x2 , x3 , x4 ) |
x1 можно исключить из f |
и q2 , подста- |
|
вив вместо нее L1 : |
|
|
|
x2 h2 (x3 , x4 )
Тогда, f (x3 , x4 ) - задача безусловной оптимизации. Находим x3 , x4 вычис-
ляем x2 |
x1 |
Метод исключения. Численное решение:
f (x1 , x2 ) |
min |
|
a1 x1 a2 x2 |
b |
|
g(x1 , x2 ) a1 x1 a2 x2 b |
точка min должна лежать на прямой. |
|
|
|
x2 |
|
|
g(x) |
|
x1 |
В каждый момент линия уровня будет касаться прямой |
эта точка и является |
точкой
условного локального min. Если в окрестности заданной точки, удовлетворяющей
всем значениям равенства, значение функции больше, чем в точке, то эта точка
– есть точка условного локального min.
25

Пример:
a1 x1 a2 x2 0 (a,x)=0
a x
x2
a |
|
x |
x1
Если (a1x)=b
x2
a |
x0 |
x x0 |
x1
Допустим, b (a1 x0 )
(a, x) (a, x0 ) 0 (a, x x0 )
Прямая будет проходить через некоторую точку удовлетворяющую условию и
a |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Для n переменных f (x) |
min , Ax=b |
|||||||
|
Рассмотрим i-ое ограничение: |
||||||||
|
|
ai1 x1 ai2 x2 |
... ain xn |
0, (a, x) 0 |
|
|
|||
|
a - задан |
x - все вектора, лежащие a . Они и составляют гиперплоскость. |
|||||||
При добавлении еще одного условия, уменьшаются размерности. В конечном итоге получится пространство n-m.
Для двух переменных возможно 2 случая:
26

1. |
2. |
В случае 2 это не точка минимума, а седловая точка.
Рассмотрим точку 3-х переменных:
x3
|
gradf |
Ограничение – плоскость, следовательно, все |
|
допустимые точки на плоскости. |
|
|
|
|
плоскость |
|
Если угол grad не равен 90 градусам следо- |
|
вательно можно двигаться дальше. На плоскости |
|
|
|
|
|
|
существует направление, которое будет составлять |
|
|
острый угол с – grad, и двигаясь в этом направле- |
|
|
нии можно уменьшить значение f. |
|
|
Если -grad f перпендикулярен плоскости эта |
x2 |
|
точка может быть точкой минимума. |
|
|
x1
Пусть существует 2 ограничения:
|
f x |
min |
|
a11 x1 |
a12 x2 |
a1n |
b1 |
a21 x1 |
a22 x2 |
a2n |
b2 |
Рассмотрим опять случай 3-х переменных:
Точка минимума должна принадлежать пересечению плоскостей. Необходимое условие – вектор антиградиента должен составлять угол 90 гра-
дусов с прямой пересечения плоскостей.
Для п-мерного случая имеется п переменных следовательно рассматривая каждое ограничение, получаем п-1 гиперплоскость следовательно рассмотрев т ограничений получим п-т гиперплоскость (т<п).
a11 x1 |
a12 x2 |
a1n |
b1 |
Ax b |
|
a21 x1 |
a22 x2 |
a2n |
b2 |
||
все ограничения |
|||||
|
|
|
|
||
|
|
|
независимы |
||
|
|
|
|
||
|
|
|
|
||
am1 x1 |
am2 x2 |
amn |
bm |
|
27

Если вектор grad (п-мерный) будет ортогонален п-т – пространству.
Допустим имеется п-1 пространство, п-мерный вектор может принадлежать ему или нет. Пусть вектор не принадлежит данному подпространству следовательно его можно разложить на 2 вектора – один который принадлежит подпространству, и второй который ортогонален данному. Ортогональное дополнение – вектора, которые ортогональны данному подпространству.
В3D – пространстве, если подпространство равно 1 следовательно ортогональное дополнение равно 2.
Вп-т-мерном подпространстве ортогональное дополнение имеет размерность
т.
Необходимое условие: Если мы находим точку, где вектор градиента принадлежит ортогональному дополнению к пространству, заданному ограничениями – равенствами, то эта точка может быть точкой локального минимума.
Пусть есть 2 плоскости. Если записать систему ограничений равенств следующим образом:
a1 , x b1 a2 , x b2 am , x bm
где ai ai1 , ai2 , , aim
Т.о. вектора a1 , a2 , , am порождают ортогональное дополнение. Существую-
щие могут быть выбраны в качестве базиса ортогонального дополнения следовательно градиент принадлежит ортогональному дополнению:
|
|
|
|
|
|
|
gradf |
1 a1 |
2 a2 m am |
||||
т.е. линейная комбинация базисных векторов.
v
V  1 a1
1 a1  2 a2
2 a2
a1
a2
1 |
2 m - множители Лагранжа. |
Рассмотрим матрицу АТ , в ней а1 , , аm - столбцы.
gradf AT 
это условие может быть использовано для численного решения задачи оптимизации с ограничивающими уравнениями.
28

Пример: |
f x |
min |
|
Ax |
b |
||
|
Ax b
AT  gradf
gradf
Если найдем такие вектора х и , для которых эти условия выполняются то точка может быть точкой локального минимума.
Рассмотрим случай когда система ограничений – равенств нелинейная:
f x1 , , xn |
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g1 x1 , , xn |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
x |
min |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gm x1 , , xn |
|
0 |
|
|
|
|
|
|
g x |
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если функции дифференцируемы, то в окрестности точки минимума |
|||||||||||||||||||
они будут вести себя как линейные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gi |
x O |
|||||||
|
x |
K |
|
g x* |
|
x g x* |
|||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
x j |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
следовательно в окрестности точки ло- |
|||||||||||||||||
|
|
кального минимума эта зависимость ли- |
|||||||||||||||||
|
|
нейная следовательно получается система |
|||||||||||||||||
|
|
вида: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x* |
|
|
x* |
x O , |
||||||
|
|
|
|
А х g |
i |
|
g |
i |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
где |
А |
|
|
gi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x j |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
следовательно необходимое условие локального минимума: xn
n-m
|
x1 |
|
|
|
|
|
x2 |
gradf |
1 gradg1 |
|
|
|
2 gradg2 m gradgm |
||
1 |
2 m - множители Лагранжа. |
||||||
|
|
|
|
|
|
|
|
|
f |
|
x |
min |
|||
|
|
|
|
|
|
||
|
|
g x |
0 |
||||
29

|
|
|
|
|
gradf |
1 gradg1 |
|
2 gradg2 |
|
|
|
m gradgm |
|||||
|
|
|
|
|
|
х* - точка может быть искомой в задаче |
|||||||||||
|
|
|
|
|
|
1 |
2 |
m - множители Лагранжа. |
|||||||||
n |
|
gradf |
1 gradg 1 |
2 gradg 2 |
|
m gradg m |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
m |
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
g x 0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
xT y ; |
|
|
|||||||
Обозначения для скалярного произведения x, y |
|
|
|||||||||||||||
|
|
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
x, y x1 , , xn |
|
xi yi ; |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
yn |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L x, y |
f x |
T g x |
f x |
1 |
g x |
m |
g |
m |
x |
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
Необходимое условие точки локального минимума исходное задание с ограничениями представляет собой необходимое условие точки локального экстремума для функции Лагранжа.
L |
f x |
|
g |
|
x |
|
|
g |
|
x |
f |
|
|
g1 |
|
|
gm |
0 |
||
x j |
1 |
1 |
|
m |
m |
x j |
1 |
x j |
m |
x j |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
L |
gi |
x |
|
|
0, i |
1, , m |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x j |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Метод множителей Лагранжа.
Применяется для нахождения точки локального минимума для точек исходной задачи h x,
 f x
f x T g x . Экстремальными точками локального минимума являются седловые.
T g x . Экстремальными точками локального минимума являются седловые.
Пример:
Найти расстояние от точки до прямой в 3-х мерном пространстве.
Плоскость : |
а11 x1 |
a12 x2 |
a1n |
b1 |
||||||
a |
21 |
x |
a |
22 |
x |
2 |
a |
2n |
b |
|
|
|
1 |
|
|
|
2 |
||||
y
Пересечение плоскостей – линия d |
x |
y 2 |
x |
2 |
y |
2 |
x |
3 |
y |
2 |
min |
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
2 |
|
|
3 |
|
||
Z x |
y 2 |
x |
2 |
y |
2 |
x |
3 |
y |
2 |
min |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
30
