
Методы и теория оптимизации.-1
.pdf
Скалярное произведение векторов a,b

 a
a


 b
b
 cos a b , где
cos a b , где 

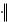 - длина вектора
- длина вектора
(норма вектора), a b - угол между векторами.
|
а |
|
а, a 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Допустим, что: a |
a1 , a2 , , an |
, b b1 ,b2 , ,bn |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
Тогда: a, b |
a b |
; |
а |
|
|
a2 |
||||
|
|
|
|
i i |
|
|
|
|
i |
|
|
|
|
|
i 1 |
|
|
|
i |
|
|
Допустим, что имеется 2 вектора:
Чтобы задать направление, мы задаем вектор.
t |
Нормируем вектор |
|
|
|
S |
|
|
|
|||||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
S
Нормированный вектор имеет тоже самое направление, но 

 1, длина.
1, длина.
Допустим, что задан нормированный вектор 

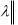 1.
1.
а |
а |
, а |
|
а |
|
cos a |
|
|
|
|
|||||
|
Скалярное |
|
|
произведение |
|||
|
равно 0, тогда года cos a |
пря- |
|||||
|
мой. |
|
|
|
|
|
|
отрицательный
Возвращаемся к функции 2-х переменных:
11

f x1 |
x2 , x2 |
x2 |
f x1 |
, x2 |
f |
x1 |
f |
x2 |
O |
|
|
||||||||
x1 |
x2 |
gradf
Отбрасываем члены О , приращение будет более точным.
х2
хх
х2 |
х х1 , х2 
|
х |
х1 , х2 |
|
х |
|||
|
|
х1
х1
Вектор gradf |
f |
; |
f |
|
|
||
|
x1 |
x2 |
|
Тейлора.
х2 |
|
х |
|
||
|
|
|
х1
f x  x
x f x
f x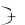 gradf , x
gradf , x O
O  - формула
- формула
1
Мы рассматриваем как изменяется точка вдоль данного направления.
Функция становится функцией одной переменной.
х - скалярная величина.
f x |
x |
f x |
gradf , x O |
f |
gradf , x - производная по направлению (вдоль данного направления) |
||
x |
|||
|
|
||
max |
f |
- направление ряда равное направлению grad ( 0). |
|
|
x |
|
|
grad – вектор, в сторону которого функция изменяется более быстро. Антиградиент – grad направленный в другую сторону (-grad).
х2
|
|
grad f |
|
f(x) |
Необходимое условие: |
х2 |
|
gradf 0 - локальный мини- |
|
|
мум (или максимум). Точки локаль- |
-grad f |
ного экстремума. |
|
12
х1
х1 |
|
|
|
|
|
|
Допустим что мы совершаем малое перемещение |
х . В каком случае (в |
|||
точке) |
будет: |
* больше, |
чем |
заданная: тогда, когда |
угол – острый |
f x |
x f x |
gradf , x |
O |
0 . |
|
*- если под прямым углом, то не изменяется;
*- если под тупым углом, то приводит к уменьшению функции.
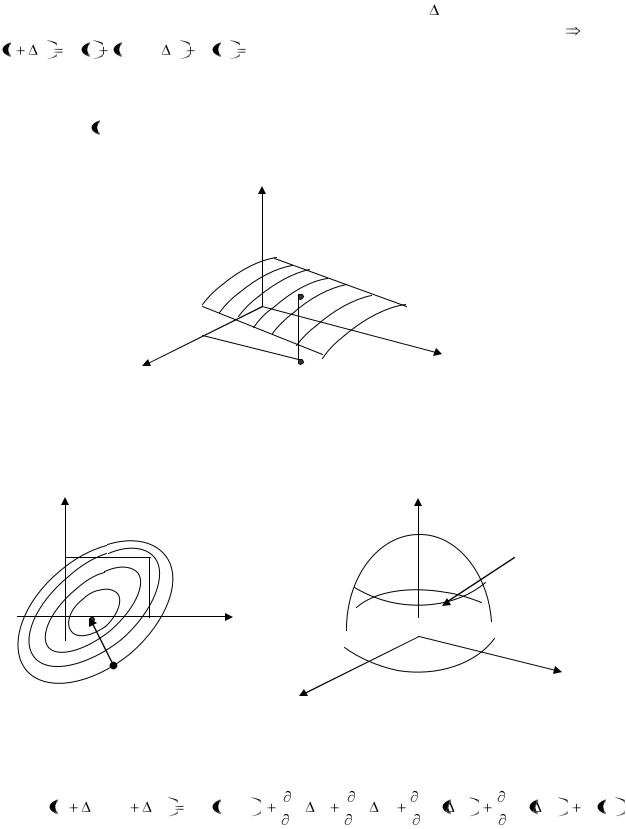
1. у  f х1 , х2
f х1 , х2 
строим поверхности
z
y
x
2. Идет построение в плоскости х1 и х2. Берут точку – определяющую значение аргумента. Находят точку в которой функция имеет тоже самое значение, в результате получаем линию в которой функция имеет постоянное значение – изолиния (линия уровня).
х2 |
z |
х2 |
изоли- |
|
ния |
х1
х1
- изолиния
y
x
Вектор grad составляет прямой угол с изолинией. Вернемся к формуле:
f x |
x |
, x |
|
x |
|
f x , x |
|
f |
x |
f |
x |
|
2 f |
x 2 |
2 f |
x |
2 |
O |
2 |
2 |
2 |
|
|
2 |
2 |
2 |
2 |
||||||||||
1 |
2 |
|
|
1 |
x1 |
1 |
x2 |
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x1 |
|
x2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
постоянный |
член |
|
|
|
|
|
|
|
|
|
|
|
Квадратичная аппроксимация.
13

|
|
|
|
|
|
(или квадратичное приращение) |
||||
Линейное отображение: |
|
|
|
|
||||||
|
|
|
|
|
|
|
L : R m |
R n ; |
|
|
|
|
|
|
|
|
|
x |
R m ; |
|
|
|
|
|
|
|
|
|
y |
R n |
|
|
|
|
|
|
|
|
|
|
|||
|
|
y |
y x - линейное отображение, если: |
|
||||||
1. |
свойство аддитивности - |
x y |
x |
y ; |
||||||
2. |
свойство однородности - |
kx |
k |
x |
|
|||||
Линейное отображение можно задать матрицей: |
||||||||||
y |
Ax |
|
|
|
|
|
|
|
||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
y |
A Bx ; C |
AB ; |
|
|
|
|
|
|
|
|
|
||||
|
п |
|
|
a j |
|
aik bkj |
- основная формула |
|||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
i |
1 |
j
|
A : R n |
R n отображение |
y |
Ax |
yi |
aij x j |
Z By BA x |
|
||||
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
2 задачи: |
|
|
|
|
|
|
|
|
|
|
|
|
- решение системы уравнений |
|
|
|
|
|
||||||
|
y |
Ax |
|
линейный |
вектор |
х |
|
|
|
|||
|
и обратное отображение – найти х |
|
|
|
||||||||
|
А-1 – обратное отображение; |
|
|
|
|
|||||||
|
АА 1 |
I |
|
A 1 A следовательно строки матрицы ортогональны столбцам |
||||||||
|
другой матрицы |
|
|
|
|
|
|
|
||||
|
- нахождение собственных значений |
|
|
|
|
|||||||
|
Используя матрицу можно найти более сложную функцию : |
Z Ax, x - |
||||||||||
квадратичная форма. |
|
|
|
|
|
|
|
|
|
|
||
|
Z |
Z x |
|
Z x1 , x2 , , xn |
- |
функция |
нескольких |
переменных |
||||
Z |
aij xi x j . |
|
|
|
|
|
|
|
|
|
|
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим подробнее. |
|
|
|
|
|
|
|
||||
|
Есть матрица: |
А |
2 |
3 |
|
|
|
|
|
|
||
|
1 |
4 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
14

Z |
2x1 x1 3x1 x2 |
1x2 x1 4x2 x2 - квадратичная форма |
||
Z |
2x2 |
2x x |
2 |
4x2 |
|
1 |
1 |
2 |
|
A' |
2 |
2 |
|
|
0 |
4 |
|
|
|
|
|
|
||
А и А/ определяют одну и ту же квадратичную форму следовательно значения этой формы не однозначно. Если по заданной квадратичной форме найдем симметрию, то она будет однозначная.
|
|
12 А |
АТ |
; |
|
|
|
|
|
А |
|
|
|
|
|
||||
АТ |
2 |
1 ; |
1 |
|
|
|
2 |
1 |
|
А А |
|||||||||
|
|
3 |
4 |
2 |
|
|
|
1 |
4 |
|
|
|
|
|
|
||||
Без ограничения общности можно считать, что матрица определяющая квадратичную форму является симметричной.
Вернемся к квадратичной форме:
Z Ах, х
Ах, х
 aij xi x j
aij xi x j
ij
Рассмотрим функцию 2-го порядка:
Z а11x12 2а12x1 x2 а22x22
Допустим, что а12 0 , матрица диагональная.
1. а11 , а22 0
x2
Эллипти-
x1 |
|
ческий |
|
парабалоид |
|
|
|
|
|
Эл- |
0 |
|
|
|
липсы |
|
|
2. а11 , а22 0
15

3. а11 0, а22 0
xx
x2
Гиперболы |
Седло |
|
Допустим, что а12 0 . Тогда вся картина просто повернется на некоторый угол по оси Z.
Рассмотрим п-мерный случай.
Квадратичная форма называется положительно определенной областью если она не отрицательная.
1.Ах, х 0 , причем обращается в ноль, в том случае если х = 0
|
( Ах, х 0 |
х 0 ). Этот случай соответствует эллиптическому параболоиду. |
|
2. |
Ах, х 0 , Ах, х 0 |
х 0 . |
|
3. |
Знаконеопределенность. |
|
|
Ах, х 0 соответствует п-мерному эллиптическому гиперболоиду (п-
мерное седло)
Рассмотрим 2-мерное пространство:
Z 0x12 x22
Если квадратная матрица называется положительно определенной, то и матрица положительно определенной.
Рассмотрим разложение функции 2-х переменных в ряд Тейлора:
f x |
x |
|
, x |
|
x |
|
f x , x |
|
f |
x |
f |
|
|
x |
|
2 |
f |
x |
2 |
2 f |
|
х х |
|
||||
2 |
2 |
2 |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
||||||||||
1 |
|
|
|
1 |
x |
1 |
|
x |
|
|
|
|
x2 |
1 |
|
x |
х |
1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 f |
|
x2 |
|
2 |
|
O |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
квадратичная матрица задается матрицей Н
16

f x  x
x f x
f x gradf , x
gradf , x Н х, х
Н х, х O
O  0
0
матрица составленная из членов 2-го порядка
|
|
|
2 f |
|
2 |
f |
|
|
|||
Н |
|
x 2 |
|
x |
x |
|
- матрица симметрична |
||||
|
|
1 |
|
|
1 |
|
2 |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
2 f |
|
|
2 |
f |
|
|
||
|
|
x |
2 |
x |
|
x 2 |
|
|
|||
|
|
|
1 |
|
|
|
2 |
|
|
||
Матрица Н – матрица Гесса.
hij |
2 f |
- определение матрицы Гесса |
||
xi |
x j |
|||
|
|
|||
Если матрица (матрица Гесса) в точке локального экстремума положительно определена, то это точка – локального минимума, если матрица отрицательно определена, то это точка – локального максимума, а если не определена – седловые точки.
Локальный max или min
Седловая точка
Минимизируем: |
|
|
|
|
||||
f x , x |
2 |
|
2x2 |
cos x x |
2 |
3x2 |
min |
|
1 |
|
1 |
1 |
2 |
|
|||
Найти частные производные: |
|
|||||||
1. |
|
|
f |
4x1 |
x2 sin x1 x2 |
0 (grad = 0); |
||
|
|
|
||||||
|
|
x1 |
||||||
|
|
|
|
|
|
|
|
|
2. |
|
|
f |
6x2 |
x1 sin x1 x2 |
0 |
||
|
|
|
||||||
|
|
x1 |
||||||
|
|
|
|
|
|
|
|
|
Эта система позволяет найти все точки экстремума:
f |
|
4x1 |
x2 sin x1 x2 |
|
|
|
|
те х1 и х2 которые удовлетворя- |
|||
x1 |
|||||
|
|
|
ют уравнениям и будет точками экстре- |
||
f |
|
|
|
||
|
6x2 |
x1 sin x1 x2 |
мума. |
||
|
|
||||
x1 |
|
||||
|
|
|
|
17

|
Допустим, что х* |
3,5 х* |
2,7 . Надо составить функцию второго порядка и |
||||
|
|
|
|
|
1 |
2 |
|
подставить х* |
х* |
и посмотреть их. |
|
||||
|
1 |
2 |
|
|
|
||
|
Необходимые условия – помогают охарактеризовать искомую точку: |
||||||
1. |
grad f = 0 |
|
|
|
|||
2. |
H |
|
f |
|
|
|
|
|
|
|
|
|
|
||
xi |
x j |
|
|
|
|||
|
|
|
|
|
|||
Н0 – локальный минимум;
Н0 – локальный максимум;
Н– не определена – седловая точка.
Для поиска используют численные методы.
Постановка: |
|
Требуется f x |
min , где х – вектор x x1 , , xn - т.к. нет ограниче- |
ний задача безусловной оптимизации.
Есть черный ящик, который по заданным значениям х позволяет вычислить значение функции.
18

Занятие № 5. МЕТОДЫ НУЛЕВОГО ПОРЯДКА
x2
y1 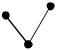 y2
y2
x0K
x1
yn
Должны задать начальное приближение точки х0;
х к - некоторое приближение полученное после к – итераций;
вычислить значение точки в окрест-
ности точки х к ; Из данных точек выбрать точку в ко-
торой функция принимает наименьшее значение, выбираем ее и строим вокруг нее окрестность.
Выбираем точку где хуже. В окрестности существующей точки выбираем точку с меньшим значением, опять в ее окрестности есть точки с меньшим значением и т.д.
В таком виде этот метод не эффективен.
Пример:
Шаг по х1 берем больше, а по х2 – сохраняем. Поскольку мы свободны в выборе точек, то можно менять шаг и направление.
Методы:
1.Хука-Дживса;
2.Нелдера-Мида (используется п-1 угольник)
Преимущества метода прямого поиска:
1.простота;
2.не нужны производные.
Недостатки:
1.плохая сходимость;
2.применим для небольшого числа переменных.
п10 20
2п точек:
в случае 2-х переменных – 4 точки; в случае 3-х переменных – 6 точек.
Этот метод применим в простых случаях, когда эти недостатки себя не прояв-
ляют.
Метод координатного спуска.
19

|
x2 |
|
|
x K |
4 |
|
Существует приближенная точка |
|
|
||
|
|
|
минимума. Минимизируя функцию по |
|
|
|
направлению к х1, на прямой использует- |
|
|
|
ся любой метод одномерной минимизи- |
|
|
|
|
|
x K |
2 |
руют, х2 – фиксируют. Далее выполняют |
|
одномерную оптимизацию по х2, фикси- |
||
x K |
3 |
|
|
|
руя х1. |
||
|
|
|
|
|
xK |
x K 1 |
|
x1
Этот процесс повторяют до тех пор пока следующая точка не окажется близка к точке приближения.
20
