Математика.-7

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Задача 93. Вычислить вычет

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Ответ.

полюс 4-го порядка.

Вычеты.

Напомним формулы вычисления вычетов, доказанные в лекциях.

полюс порядка 1:

Re s

f (z) =

lim

(z z0 ) f (z) .

z z

(m 1)

полюс порядка m:

Re s

f (z) =

lim (z z

0 )

f (z)

z z0

(m 1)! z z0

z 2 f (z)

устранимая особая точка:

Re s f (z) lim

полюс порядка m:

Re s f (z)

( 1)m

lim

z m 2

f (m 1) (z)

(m 1)! z

Задача 84. Вычислить вычет

	Re s	z
	Re s	(z i)(z 2i)
	z i	(z i)(z 2i)

Решение.

Точка z i

является полюсом 1-го порядка. Вычисляем по

формуле

Re s f (z) =

lim

(z z0 ) f (z) .

z z

Re s

= lim

(z i)

= lim

z i (z i)(z 2i)

z i

(z i)(z

2i)

z i z 2i

Ответ.

Задача 85. Вычислить вычет

Re s

(z i)

(z 2i)

z i

Решение. Точка z i

является полюсом 2-го порядка. Вычисляем по

lim (z z0 )

(m 1)

формуле

Re s f (z) =

f (z)

при

m 2 .

z z0

(m 1)! z z0

Более конкретно эта формулы выглядит так:

lim (z z0 )

Re s

f (z)

f (z) .

этом конкретном

примере

z z0

1! z z0

получается

Re s

= lim

(z i)

(z 2i)

(z i)

z i

2i)

z 2i z

lim

= lim

z i

z 2i

(z 2i)

2i)

(3i)

z i

Ответ.

Задача 86.

Вычислить вычеты во всех особых точках и в

для

функции

f (z)

1)(z

Решение. Особые точки здесь 1 и

, полюсы 1 порядка.

Re s

lim

= lim

z 1

(z 1)(z 2)

z 2

z 1

Re s

lim

(z 2)

= lim

z 2

(z 1)(z 2)

z 2 z

z 2

Для вычисления Re s

z (z 1)(z

Способ 1. Использовать тот

покажем 2

факт, что	Re s
	z

способа:

противоположен сумме

всех вычетов в конечных особых точках. Тогда

Re s

1)(z 2)

z 1

(z 1)(z 2)

z 2

(z 1)(z 2)

= 1.

Re s f (z) lim z 2 f (z) . Заметим, что здесь

Способ 2. По формуле

является

устранимой особой точкой, ведь

lim

т.к.

1)(z 2)

z (z

степень числителя меньше степени знаменателя.

Re s f (z) lim z		2	f (z)
Re s f (z) lim z			f (z)
	z

					z
lim	z	2
				2
z			z		z 2

2) (2z 1)z

lim

z 2)

lim

т.к.

старшая

степень

...

числителе, и в знаменателе. Соотношение старших степенях равно 1.

	z		2	2
2						=
2					2
(z	2	z 2)
	2

одна и та же и в коэффициентов при

Ответ.

Re s f

z 1

1 3

Re s f

z 2

2 3

Re s f


																							sin			z
Задача 87. Вычислить вычет																						Re s		2					.
Задача 87. Вычислить вычет																						Re s					3		.
																						z 3	(z 3)				3
																						z 3	(z 3)
Решение. Точка														z 3			является полюсом 3 порядка.
При этом формула приобретает вид (при m 3 ):
											1								3
Re s f (z)								=					lim (z z0 )						3		f (z) .
Re s f (z)								=					lim (z z0 )								f (z) .
z z0										2! z z0


				sin				z														sin		z
							2							1			(z				3		2							1
Re s											=				lim				3)										=			lim sin
Re s											=				lim				3)										=			lim sin
z 3					(z 3)				3													(z 3)			3
z 3					(z 3)									2! z 3								(z 3)									2 z 3


1																1																		2
																																		2
															=																	=
			lim cos										z		=							lim sin						z				=
										2						2		2								2							8
2 2 z 3										2						2		2		2 z 3						2							8
		2			1							2
								=					.
	8							=			8		.
	8										8
Ответ.						2			.
Ответ.							8		.
							8



	z
2
2

3
sin
	2

Задача 88. Вычислить вычет					1
Задача 88. Вычислить вычет			Re s sin

			z 0	z
Решение. Здесь	z 0	существенно			особая точка (см. аналогично

задаче 80). Поэтому ни одна из формул не подходит, а можно найти

только с помощью коэффициента

a 1 ряда Лорана.

Разложим в ряд Лорана:

1 1

sin

5 ..., здесь коэффициент a 1 1 .

3! z

5! z

Ответ. 1.

Задача 89. Вычислить вычет Re s

(z 1)

z 1

Решение. Несмотря на то, что видим здесь

(z 1)

, тем не менее,

полюс

z 1

не 2-го порядка, потому что в другом множителе тоже

присутствует

(z 1) .

			z								=							z					=
(z 1)			2	(z	2			1)			=	(z 1)			2	(z 1)(z					1)		=
			2		2										2									(z
																								(z
Таким образом,											z 1			полюс 3 порядка.
Таким образом,														полюс 3 порядка.
											z						1				z
											z						1				z
Тогда Re s															=				lim				=
Тогда Re s										1)3					=				lim				=
				z 1 (z						1)3		(z 1)						2! z 1 z 1
1					1							1					2					1 2
1					1							1					2					1 2
	lim										=		lim								=
	lim								2		=		lim							3	=				3
2		(z					1)		2			2 z 1 (z 1)										2		2
	z 1
Ответ.						1		.
Ответ.								.
					8

		z
1)		3	(z
1)			(z
1				(
	lim
2
2
	z 1

=1 . 8

1)
z 1) z
z 1) z

(z 1)	2
(z 1)

Практика № 11.	19.11.2018
		z	2
Задача 90. Вычислить вычет Re s		z
Задача 90. Вычислить вычет Re s		(z 2)
	z	(z 2)

Решение. (2 способа).

1)	С помощью перехода к конечным особым точкам.
2)	С помощью формулы в .

Способ 1. Заметим, что здесь всего одна особая точка в плоскости, это z 2 . Таким образом, вычет в противоположен вычету в z 2 . Этот метод очень удобен, когда мало конечных особых точек. Но наоборот, неудобен, когда слишком много особых точек, т.е. когда в знаменателе многочлен большой степени, когда даже поиск корней будет слишком сложной проблемой.

		z	2			z	2
Re s		z		=	Re s	z
Re s		(z		=	Re s	(z 2)
z		(z		2)	z 2	(z 2)
z	2			= 4 .
	2
		z 2

			z 2
=	lim	(z 2)		=
=	lim	(z 2)		=
			(z 2)
	z 2		(z 2)

lim	z	2

z 2

Способ 2. По формуле. Тогда надо сначала определить порядок полюса m, чтобы знать, какую формулу применить.

f (z)

z	2

(z 2)

. Если сделать замену

1 z

, то можно будет 1

исследовать порядок полюса в точке t 0 . Итак,

f (t)		t	2

	1
		2
	t

. Полюс t 0 порядка 1, а значит и

1 2t

t(1

2t)

полюс порядка 1. Впрочем, это можно было заметить и по виду

функции: степень числителя на 1 больше, чем знаменателя.

Итак, надо применить формулу для полюса при m 1.

Re s f (z)

( 1)m

lim z m 2

f (m 1) (z) при m 1.

(m 1)! z

Конкретизируем её для m 1.

Re s			f (z)					1		lim				z	3	f						Найдём 2-ю производную. Всё делаем по
															3
								2!										(z) .
								2!		z
						u

												u v			v u					.
формуле																2				.
						v								v		2
						v								v
f (z)						z 2													2z(z 2) z 2												z 2	4z
								,				f																		=					.
								,				f		(z)										2						=				2	.
					z 2																(z		2)	2							(z 2)			2
					z 2																(z		2)								(z 2)
					(2z				4)(z						2)		2	2(z 2)(z							2		4z)					(2z 4)(z 2)							2(z	2	4z)
f					(2z				4)(z						2)			2(z 2)(z									4z)				=	(2z 4)(z 2)							2(z		4z)

	(z)															(z 2)					4																	(z 2)	3
																					4																		3

	2z		2	8z				8			2z			2	8z							8
=	2z			8z				8			2z				8z					=		8				. Тогда
=						(z			2)		3									=	(z		2)	3		. Тогда
											3													3

								1		lim z																						1						8
Re s			f (z)					1							3	f								=								1	lim			z	3	8			=
															3																						3
								2!										(z)														2						(z 2)	3
										z																							z						3
																																	z

	1									8z			3										1
	1	lim								8z												=	1	8				=		4 .

	2					z	3	6z			2	12z 8											2
							3				2
		z

Ответ.					4			.
Ответ.								.
																											z		4
Задача 91. Вычислить вычет Re s																											z			.
Задача 91. Вычислить вычет Re s																										4				.
																						z		z		4			1
																						z		z					1

Решение. (2 способа).

Способ 1. С посощью перехода к сумме вычетов в конечных точках.

	z	4

z	4	1

		z	4
		z
(z	2	1)(z		2	1)
(z		1)(z			1)

i)(z

z	4

i)(z

1)(z

. Здесь 4 особых

точки, это

1,i

		z	4
Re s
		4	1
z	z

			z 4
Re s					Re s
Re s			4		Re s
	z i	z	4	1	z i
	z i	z		1	z i
		z		4
		z
	(z i)(z 2 1)
	(z i)(z 2 1)					i
						i

z 4	Re s	z 4	Re s	z 4
z 4 1		z 4 1
	z 1		z 1 z 4 1

z 4			z 4
(z i)(z 2 1)	i	(z 2	1)(z 1)
(z i)(z 2 1)		(z 2	1)(z 1)


	=


				z	4
				z
		(z	2	1)(z 1)
			2
1						1

=	1	1	1	1
=
	2i( 2)	2i( 2)	2 2	2 ( 2)
	2i( 2)	2i( 2)	2 2	2 ( 2)

противоположны, и 3-е с 4-м тоже.

= 0, т.к. 1-е и 2-е слагаемое

																		z		4
Способ 2. По формуле.														lim				z				= 1, то								устранимая особая точка.
Способ 2. По формуле.														lim				4				= 1, то								устранимая особая точка.
														z z				4		1
														z z						1											z 2		f (z) .
Тогда надо считать по формуле																					Re s f (z) lim										z 2		f (z) .
																													z
	z	4			4z	3	(z		4		1) 4z					3	z	4				4z				3
		4				3			4							3		4								3


	4	1	=					(z			4	1)		2						=		(z	4	1)				2 , тогда
z		1						(z				1)										(z		1)
											4z 3													4z 5
Re s f (z) lim						z 2												=			lim									= 0 , т.к. наивысшая
Re s f (z) lim						z 2						4			2			=			lim				8					= 0 , т.к. наивысшая
										(z		4	1)		2										8		...
				z						(z			1)								z z						...
степень в числителе 5-я а в знаменателе 8-я.
Ответ. 0.
Задача 92. Вычислить вычет																		Re s									1					.
Задача 92. Вычислить вычет																		Re s									3				2	.
																			z 7			(z 7)					3	(z		5)	2
																			z 7			(z 7)						(z		5)

Решение. Здесь 7 это полюс 3-го порядка. Тогда надо использовать

		1			m	(m 1)
формулу Re s f (z)	=		lim	(z z0 )		f (z)	, которая при

z z0		(m 1)! z z0

m 3		выглядит так:						Re s
								z z	0
									0
Итак,		Re s			1
Итак,		Re s			3				2
		z 7 (z 7)			3	(z 5)			2
		z 7 (z 7)				(z 5)
1		1					1
1		1					1
	lim				=			lim
	lim	(z 5)		2	=			lim
2 z 7							2 z 7


3 =		3	.
3 =			.
2	4	16
2		16

Ответ. 163 .

				1	lim (z z0 )				3
f (z) =									3	f (z) .
f (z) =										f (z) .
				2! z z0
	1										1
=	1	lim			(z 7)3						1
=		lim			(z 7)3						3				2
								(z 7)			3		(z	5)	2
	2! z 7							(z 7)					(z	5)
( 2)						1		( 2)( 3)
( 2)						1		( 2)( 3)
					=		lim							=
(z 5)			3		=	2	lim	(z 5)				4		=
(z 5)						2	z 7	(z 5)						(z
							z 7

	3
	5)	4
	5)	7
		7

Решение. В отличие от прошлой задачи, здесь

так что формула										Re s				f (z)			=		1			lim		(z z0 )				m
																												m

											z z0							(m 1)! z z0
	приобретёт вид: Re s f (z) =																	1	lim (z z0 )						4		f (z)
																									4

										z z0								3! z z0
						1								1					1				(3)		1
						1								1					1						1
Re s													=											=			lim
Re s						4	(z		5)		2		=	3!	lim			(z 5)			2			=	3!		lim
	z 7		(z 7)				(z		5)					3!				(z 5)							3!		z 7
	z 7														z 7												z 7
1				( 2)( 3)									1		( 2)( 3)( 4)											1
		lim								=				lim										=			lim
		lim								=				lim										=			lim
3!		z 7		(z 5)				4					3!	z 7				(z 5)		5					3! z 7
3!				(z 5)									3!					(z 5)
			4		2		2					1				1
=			4	=	2				=			1		=		1	.
=		2	5	=		2	5		=		2		3	=		8	.
			5				5						3

полюс 4-го порядка,

	(m 1)
	f (z)

.
(3)
( 2)
( 2)
			=
(z 5)	3		=
	3

3!( 4)				4
3!( 4)			=	4

(z 5)		5		(z 5)	5
(z 5)				(z 5)	7

Ответ.

Задача 94. Вычислить вычет Re s

(z i)

z i

Решение. Здесь точка

z i полюс 2-го порядка.

lim e

Тогда

Re s

lim (z i)2

f (z)

(z i)

z i

1! z i

z i

2i e 1

Ответ.

lim 2ze	z	2
	z

z i

Приложения вычетов.

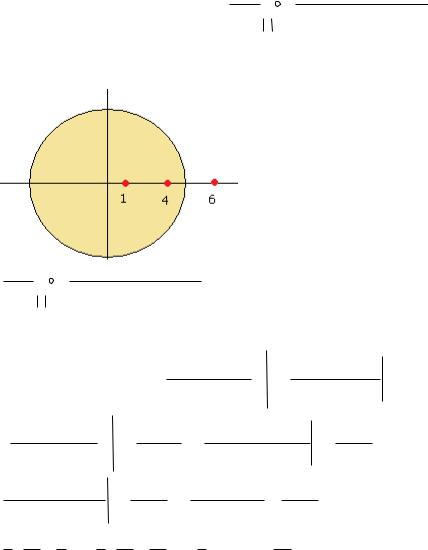
Задача 95. Вычислить интеграл

1 2

			1
	(z 1)	2	(z 4)(z 6)
z 4,5

Решение. Так как радиус равен 4,5 то точки 1 и 4 внутри круга, а 6 снаружи. Поэтому интеграл считается с помощью суммы двух вычетов, а не трёх.

	1								2	1			dz		=	Re s		f (z) Re s					f (z)	. Одна из точек
2									2				dz		=	Re s		f (z) Re s					f (z)	. Одна из точек
			i	z 4,5			(z 1)			(z 4)(z 6)						z 1				z 4
			i				(z 1)			(z 4)(z 6)

(	z 1				)	это		полюс 2-го порядка,										в том случае надо считать
(					)	это		полюс 2-го порядка,										в том случае надо считать
производную, а там где полюс 1-го порядка ( z 4 ) не нужно.
													1								1
Re s				f (z) Re s									1								1			=
Re s				f (z) Re s					f (z) =												2			=
													4)(z					(z 1)			2	(z 6)
	z 1						z 4					(z	4)(z			6)		(z 1)				(z 6)		4
	z 1						z 4
																	1
																	1
					1							1		(2z 10)									1
					1							1		(2z 10)									1
		2									2		=	2					2					=
z		2	10z 24							3	2	( 2)	(z	2	10z 24)				2		9( 2)
																				1	9( 2)

									1
									1

=	( 8)				1
	( 3)	2	( 5)	2	9( 2)

=	8	1	=

	9 25	9( 2)

1	8	1	=	1 16	25	=	1
			=			=
9 25		2		9 50	50		9

Для технического удобства перемножили в знаменателе, а

9	=	1	.
50		50

вычисления производной мы сначала потом снова разъединили множители.

Ответ.	1	.
	50

Задача 96. Вычислить интеграл

Решение. Здесь очевидно, точки как радиус равен 5.

1			1	2	dz .
2			(z 2)(z 4)
	i	z 5			(z 6)

2 и 4 внутри круга, 6 снаружи, так

1							1				dz
2	i				(z 2)(z			4)	2	(z	dz
2	i	z	5		(z 2)(z			4)		(z	6)
		z	5
			1							1
			1							1
			2
(z 4)			2	(z 6)				(z 2)( z 6)
(z 4)				(z 6)		2		(z 2)( z 6)
						2

= Re s f (z) Re s f (z) =

z 2			z 4
		1				1




=		2			2
=	( 2)	2	( 4)		2	8z 12
				z
				z
4
4

	1	(2z 8)		=		1	(2z 8)
16		(z 2 8z 12)	2		16		(z 2)2 (z 6)	2

			4					4

161 .

Ответ.

Задача

		1
		16
		16

97.

Вычислить интеграл


	(x	2
	(x

1
1)(x	2
1)(x

36)

Решение. Рассмотрим функцию f (z)		1			, её	можно

		(z 2 1)(z 2		36)

представить в виде f (z)	1		,	есть 4		полюса

	(z i)(z i)(z 6i)(z 6i)

первого порядка: i, 6i . Интеграл по границе верхнего полукруга равен сумме вычетов в 2 точках, а именно i,6i . Если радиус больше 6,

то обе точки внутри полукруга, и при дальнейшем увеличении радиуса интеграл уже не изменится. При этом из теории известно, что при увеличении радиуса, доля результата, приходящегося на горизонтальный отрезок, растёт, а по дуге - стремится к 0, потому что

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20232.61 Mб4Математика.-2.pdf
#
05.02.20232.05 Mб3Математика.-3.pdf
#
05.02.20232.49 Mб3Математика.-4.pdf
#
05.02.20233.03 Mб3Математика.-5.pdf
#
05.02.20232.78 Mб3Математика.-6.pdf
#
05.02.20232.74 Mб5Математика.-7.pdf
#
05.02.20233.16 Mб4Математика..pdf
#
05.02.2023584.83 Кб53Математическая логика и теория алгоритмов.-1.pdf
#
05.02.2023886.2 Кб7Математическая логика и теория алгоритмов.-2.pdf
#
05.02.2023671.92 Кб5Математическая логика и теория алгоритмов.-3.pdf
#
05.02.2023482.94 Кб5Математическая логика и теория алгоритмов.-4.pdf