Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика.-7

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Интегрирование функций комплексного переменного.

Задача 55. Вычислить				zdz	по отрезку от 0 до i .
Задача 55. Вычислить				zdz	по отрезку от 0 до i .
			L
Решение.	zdz	= (x iy)(dx idy) = (xdx ydy iydx ixdy)
	L	L			L

(xdx ydy) i ( ydx xdy)
L	L

а это уже 2 криволинейных интеграла

второго рода от различных векторных полей. Причём

вертикальном отрезке, соединяющем 0 с точкой i , фиксировано													x
а значит и dx 0 , т.е. исчезают все слагаемые, где есть											x или dx .
										1
При этом			y [0,1]			. Итак, (0 ydy) i ( 0 0dy) = ydy 0i						=
								L	L	0
y	2	1		1			1
	2
		0i	=		0i	=		.
2		0i	=	2	0i	=	2	.
2		0		2			2
		0

на

0 ,

Ответ.	1	.
	2

Задача 56. Вычислить		zdz	по окружности радиуса	R	.
Задача 56. Вычислить		zdz	по окружности радиуса		.
	L

Решение. Изначально преобразование с раскрытием скобок

такое же, как и в прошлой задаче:

zdz

(x iy)(dx

точно idy) =

(xdx ydy iydx ixdy) L

(xdx L

L	L
ydy) i ( ydx
	L

xdy)

Дальше, криволинейные интегралы вычисляются иначе из-за того, что

другая кривая. На окружности наилучший способ задать точку - параметрически: x Rcost , y R sin t . При этом t [0,2 ] .

Также вычислим дифференциалы: dx Rsin tdt , dy R cos tdt .

2
(R cos t(R sin t)
0
	2		2
=		0dt i			R		2	(sin	2
							2		2

	0		0			i .
Ответ. 2R				2		i .
				2

			2
R sin tR cos t)dt i ((R sin t)(R sin t) R cos tR cos t)dt
			0
					2
t cos		t)dt	= 0 iR			dt	= 2R	i .
	2			2			2
					0

Задача 57. Вычислить			z	2	dz по отрезку от 0 до 1	2i .
				2

		L
Решение. Способ 1. Без формулы Ньютона-Лейбница.
z 2 dz	= (x2 y 2 ) i(2xy) (dx idy) =
L	L
(x2 y 2 )dx (2xy)dy i (2xy)dx (x2 y 2 )dy =
L				L

Далее используем явное выражение

y 2x , так как отрезок соединяет

точки (0,0) и (1,2). При этом

dy 2dx ,

x [0,1] .

) (2x2x)2 dx i

(2x2x)

)2 dx =

0
1		1
11x	2	dx i 2x	2	dx
11x		dx i 2x		dx
0		0

0
=	11	x3	1	i	2	x3	1
			1				1

	3		0		3		0
	3				3

	11
	3
	3

	2	i
	3	i
	3

Способ 2. По формуле Ньютона-Лейбница.
Заметив, что функция z 2 аналитическая,	т.е.		для неё выполняются
условия Коши-Римана, можно не раскрывать			скобки предыдущим
способом, а вычислить первообразную по	z	в начальной и конечной

точке.

1 2i
z	2	dz
z		dz
0

1			1 2i		(1	2i)3
1		3			(1	2i)3
	z			=			0	, а дальше всё сводится просто к
3	z		0	=		3	0	, а дальше всё сводится просто к
3						3

вычислению степени комплексного числа.

(1 2i)2 3 4i (1 2i)3 ( 3 4i)(1 2i) = 11 2i , тогда

(1 2i)	3				11			2
		=							i .
3					3			3

Ответ.			11			2	i
				3		3

Задача 58. Вычислить

z	2	dz
z		dz
AB

по участку единичной окружности в 1-й

четверти от 1 до

i .

Решение. Здесь тоже можно вычислять как без, так и по формуле

Ньютона-Лейбница. Но разница в объёме вычислений будет огромная, в несколько раз в данном случае.

Способ 1. z 2 dz	=	(x2 y 2 ) i(2xy) (dx idy)	=
L		L
(x2 y 2 )dx (2xy)dy i (2xy)dx (x2 y 2 )dy , далее используем
L		L

параметрические выражения x cos t ,														y sin t			, где

2
((cos				2	t sin	2		t)( sin t) (2 cos t sin t) cos t)dt
((cos					t sin			t)( sin t) (2 cos t sin t) cos t)dt
0

	2
i		((2 cos t sin t)( sin t) (cos							2	t	sin		2	t) cos t)dt			=
									2				2

	0

2								2
(sin			3	t 3cos			2	t sin t)dt i (cos			3	t 3sin			2	t cos t)dt
(sin				t 3cos				t sin t)dt i (cos				t 3sin				t cos t)dt
0								0

0, 2

здесь в двух слагаемых из 4 можно применить подведение под знак дифференциала, а в двух других, где третья степень - замену (при нечётной степени косинуса замена s sin t , при нечётной степени синуса s cost ).

Итак,


2
sin		3
sin
0
0
	1
1


	2						2								2				2
sin			3	tdt			3cos			2	t sin tdt				i cos		3	tdt i 3sin					2	t
sin				tdt			3cos				t sin tdt				i cos			tdt i 3sin						t
0							0								0			0

				2						2								2
tdt i cos						3	tdt			3cos		2		td(cos t) i 3sin					2		td(sin
tdt i cos							tdt			3cos				td(cos t) i 3sin							td(sin
				0						0								0
		3		1				1						3	1
	2	3		1			ds i						2	3	1					3
s	2										1 s		2				ds cos			3	t	2
s			1 s		2						1 s				1 s	2	ds cos				t	0
					2			0								2						0
								0
				1
s 2 2 ds i							1 s 2		2 ds (0 1) i(1 0) =

cos tdt
t) =
isin	3	t

0					0
1					1
(1 s			2	)ds i (1 s			2	)ds 1 i
(1 s				)ds i (1 s				)ds 1 i
0					0
2	2	i 1 i			=	1		1	i .
3	3	i 1 i			=	3		3	i .
3	3					3		3

	s	3	1		s	3	1
			1				1

s				i s			1 i
	3				3
	3		0		3		0
			0				0

Способ 2. Так как функция аналитическая, нам не важно, соединены точки по дуге окружности или по какой-то другой линии, на самом деле результат зависит только от первообразной в начальной и конечной точках.

i
z	2	dz
z		dz
1

z	3	i


3		1

i	3		3
i			1
		3

= i 1 3

1 3

	1	i
	3	i
	3

	Ответ.	1
	Ответ.	3
		3

Задача 59.

	1	i .
	3

Вычислить Re( z2 )dz			по отрезку от 0 до 1 3i .

			AB
Решение.	Так	как	Re( z	2	) x	2	y	2	0i ,	то	функция не

аналитическая,		т.к. частные			производные от					u	будут какие-то
функции,	а от v	нулевые, и точно не не будет совпадений, которые

нужны для условий Коши-Римана. Поэтому формулу НьютонаЛейбница здесь применить нельзя, а только универсальный способ с

разложением на u явным уравнением

iv y

. Отрезок от (0,0) 3x , при этом dy

до (1,3), он характеризуется

3dx , x [0,1] .

Re( z	2	)dz
Re( z		)dz
AB

(x	2	y	2	)(dx idy)
(x		y		)(dx idy)
AB

(x	2	y	2	)dx i (x	2	y	2	)dy
(x		y		)dx i (x		y		)dy
AB				AB

1				1
(x	2	9x	2	)dx i (x	2	9x	2	)3dx
(x		9x		)dx i (x		9x		)3dx

	1
=
=

		1
( 8x	2	)dx i ( 24x	2	)dx
( 8x		)dx i ( 24x		)dx

0										0					0	0
	8		1			24				1	8
	8	x	3	i		24		x	3	=	8	8i .
			3						3
	3		0				3			0	3
			0							0
Ответ.					8		8i .
Ответ.					3		8i .
					3
												1 i
Задача 60.							Вычислить						(3z	2	2z 1)dz .
														2

												1

Решение. Здесь сумма степенных функций, они являются аналитическими. Поэтому используем формулу Ньютона-Лейбница.

1 i

(3z2 2z 1)dz = z 3 1

z 2

i)3 (1

i)2 (1

z 1

= (1

i) 3

Отдельно вычислим (1 i)2

(1 i)(1 i) 2i ,

(1 i)

2i(1 i) 2 2i .

Тогда

2 2i ( 2i) (1 i) 3

= 4 5i .

Ответ. 4 5i .

5 i

Задача 61. Вычислить

)dz .

	5 i			z	2	5 i
Решение.		(z 3z2 )dz	=	z		z3 5 i =
Решение.		(z 3z2 )dz	=	2		z3 5 i =
						2	2
	2					2

Вычислим квадрат и куб этого числа.							(5
(5 i)3 (24 10i)(5 i) = 110 74i .

	(5 i)	2

	2

	i)(5 i)

4	((5 i)	3	8)

2

24 10i ,

Тогда	24 10i	2	(110	74i) 8				= 12 5i 110 74i 6	=
Тогда	2	2	(110	74i) 8				= 12 5i 110 74i 6	=
	2
92 69i .
Ответ. 92 69i .
			i
				2
Задача 62. Вычислить					e	z	dz .
						z

				0

Решение. Можно применять формулу Ньютона-Лейбница, так как


функция					e	z	аналитическая.
функция					e		аналитическая.
e	z	(e	x	cos y) i(e				x	sin y) , тогда:
e		(e		cos y) i(e					sin y) , тогда:

cos y vy ,

u y e

sin y

vx .

e z dz

= e z

= e

2 e0

= cos

i sin

0 1i 1

i 1 =

Ответ.

1 i1

Практика № 8.	22 и 25.10.2018
	Интегральная формула Коши.

Следующая серия задач решается с помощью формул Коши:

f (z		)	1		f (z)		dz и	f (n) (z		)	n!		f (z)			dz .
f (z	0	)	2 i z z				dz и	f (n) (z	0	)	2 i		(z z		)n 1	dz .
	0								0
						0								0
				L		0						L		0

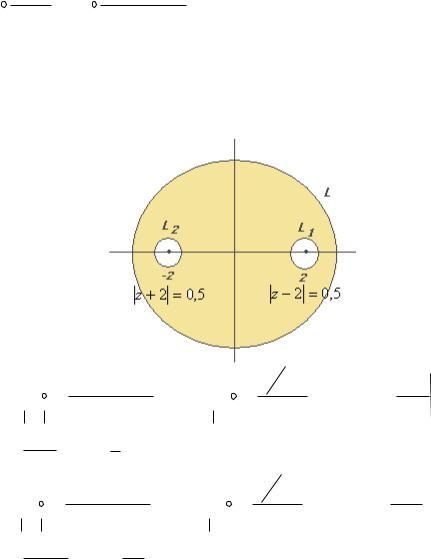
Здесь будут комбинированные задачи, состоящие из нескольких подзадач, где контур проводится сначала вокруг той или иной точки разрыва, а затем вокруг всех этих точек.

				z	3
Задача 63. Вычислить				z		dz , где контур
			z	2	4

		L
		L
А) z 2 0,5	Б) z 2		0,5			В)	z	3 .
А) z 2 0,5	Б) z 2		0,5			В)	z	3 .

Решение. В знаменателе разложим на множители, и станет видно, что корни многочлена там 2 и 2 .

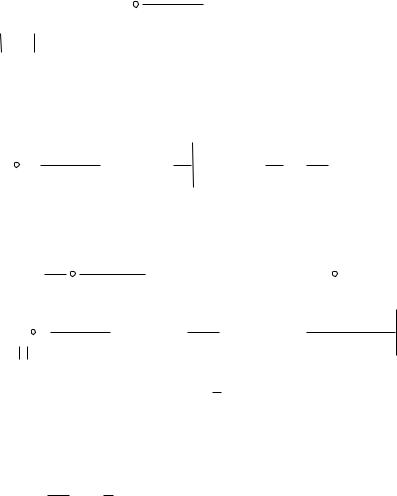
		z	3		=	z	3
				dz				dz .
	z	2	4			(z 2)(z 2)
L					L

Если контур радиуса 0,5 окружает одну из точек, интегральную формулу Коши, где точка z0 одна

то надо применить из них, а именно, в

первом пункте

, а во втором

. Надо убрать

знаменателя соответствующую скобку, и присвоить конкретное вместо z в оставшейся части функции.

из

А)

					(z
	z 2 0,5				(z
	z 2 0,5
	2	3
i	2			= 2
i	2		2	= 2
	2		2

	z	3
	z
	2)(z
	i	8
	i	4
		4

dz
2)
= 4	i

		z	3
			z 2
				dz
			z 2
z 2	0,5

	z	3
i	z
i	z 2
	z 2		z 2
			z 2

Б)

		(
	z 2 0,5	(
	z 2 0,5

i( 2)3

2 2

z	3

z 2)(

= 2

z i

2)	dz	=
2)
8	= 4 i .
4	= 4 i .
4

		z	3
			z 2
				dz
			z 2
z 2	0,5

i z

В) В третьем пункте, где контур окружает уже обе точки, будет воспользоваться теоремой Коши и суммировать двух предыдущих пунктов. Получится 8 i .

z	3
z			=
		2	=
		2	z 2
			z 2

достаточно

результаты

Ответы. А)

Б)

В)

Задача 64. Вычислить

		e	z
		e
z	2	(z 2)
z		(z 2)

, где контур

А)

z 2

0,5

Б)

z 0,5

В)

Решение. В 1 пункте здесь корень 2 соответствует z 2 0,5 , а во

втором корень 0, но он имеет кратность 2, поэтому надо будет сделать по обобщённой интегральной формуле Коши, то есть с помощью производной.

А)

= 2 i

= 2

z 2

0,5

z 2

Б)

Здесь корень 0, он соответствует множителю

, который,

впрочем, можно было бы записать в виде скобки (z 0) .

Конкретизируем обобщённую формулу Коши для 2 степени:

f (n) (z0 )

f (z)n 1

dz ,

при n=1:

f (z0 )

f (z)

2 i

2 i L (z z0 )2

L (z z0 )

(z 2) e

Тогда

2 i

(z 2)

z 0,5

z 0

2 i	e0 ( 2) e0	= 2 i	2 1	=	3	i .
	( 2)2		4		2

В) Здесь внутри контура обе особые точки, рассмотренные в предыдущих пунктах. По интегральной теореме Коши просто складываем результаты, полученные в 2 предыдущих пунктах.

	i	e	2		3	i .
Получаем					3

					2
2					2
Ответы. А)		i		e2		Б)	3	i	В)	i	e2	3	i .
Ответы. А)		2		e2		Б)	2	i	В)	2	e2	2	i .
		2					2			2		2

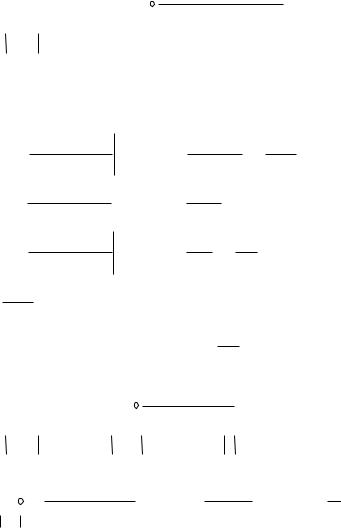
Задача 65. Вычислить


L	(z

12)(z 3)(z

, где контур

А)

z 2

0,5

Б)

z 3 0,5

В)

z 5 0,5

Г)

Решение. В каждом случае применяем интегральную формулу Коши к той или иной точке разрыва функции, 2, 3 и 5. Убирая соответствующий множитель из знаменателя, затем подставляем в оставшуюся часть функции это число.

	2			1						2	i	1					2	i
А)		i		1					=			1				=		.
А)		i				5)			=				3)			=		.
		(z 3)(z				5)		z 2			( 1)(		3)				3
								z 2
Б)	2	i		1					=	2	i	1		=			i .
				1								1
						5)
		(z 2)( z				5)		z 3			1( 2)
	2			1				z 3		2	i	1				i
																i
В)		i							=				=			.
В)		i				3)			=			2	=			.
		(z 2)(z				3)		z 5			3	2			3
								z 5
Г)	2	i	i +				i	= 0 .
Г)	3		i +			3		= 0 .
	3					3
Ответы.			А)		2 i			Б)	i		В)			i		Г)		0.
Ответы.			А)	3				Б)	i		В)		3			Г)		0.
				3									3

Задача 66. Вычислить L (z 1)3 (z 2) dz , где контур L :

А)

z 2

0,5

Б)

z 1 0,5

В)

z 3 .

Решение.

А)

= 2

(z 1)

z 2 0,5

(z 2)

z 2

= 4

Б) В этом случае корень знаменателя имеет кратность 3, так что придётся считать с помощью 2-й производной.

Конкретизируем обобщённую формулу Коши для 3 степени:

(n)

(z0 )

f (z)

dz ,

при n=2:

(

2 i

(z z

)

n 1

Тогда

= i

z 1 0,5

(z 2)

1 (z 2) 1 z

(z 2)

z0 )	2!		f (z)				3 dz
z0 )	2 i		(z z			)	3 dz
	2 i	L	(z z	0		)
		L		0
=
z 1
= i ( 2)(z 2)					2



								z 1
								z 1

i 4(z 2)

= i

i .

( 1)

z 1

В) 4 i 4 i = 0 .

Ответы.

А)

4 i

Б)

В)

0 .

Задача 67. Вычислить

, где контур

z(z 1)

А)

z 0,5

Б)

z 1 0,5

В)

z 3 .

Решение.

А)

= 2 i

= 0.

1)2

z(z 1)2

( 1)2

z 0,5

z 0

Б)

i z

= 2

i3z

z(z 1)

z 1 0,5

z 1

i .

В) 0+ 6

i .

Ответы. А) 0

Б)

В)

z 1

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20232.61 Mб4Математика.-2.pdf
#
05.02.20232.05 Mб3Математика.-3.pdf
#
05.02.20232.49 Mб3Математика.-4.pdf
#
05.02.20233.03 Mб3Математика.-5.pdf
#
05.02.20232.78 Mб3Математика.-6.pdf
#
05.02.20232.74 Mб5Математика.-7.pdf
#
05.02.20233.16 Mб4Математика..pdf
#
05.02.2023584.83 Кб53Математическая логика и теория алгоритмов.-1.pdf
#
05.02.2023886.2 Кб7Математическая логика и теория алгоритмов.-2.pdf
#
05.02.2023671.92 Кб5Математическая логика и теория алгоритмов.-3.pdf
#
05.02.2023482.94 Кб5Математическая логика и теория алгоритмов.-4.pdf