Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика.-7

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

во

2-м

	2		4	1
	2		4	sin
				sin
2		4
2		4		0
				0
слагаемом по

2	1	2 (		) d
2			3
0

	0

всё равно получается множитель 0, поэтому

интеграл по				можно и не вычислять.
1			1	1				1			3
1			1	0 2 (	3	) d = 3		1			3
3 2							2		0	=		.
3 2							2		0	=		.
2			4	0				4			2
				0
Ответ.	3	.
Ответ.	2	.
	2
				Потенциал векторного поля.

В следующих задачах найти потенциал, либо доказать, что поле не потенциально:

Задача 24. F ( yz, xz, xy) .

Решение.

Чтобы доказать, что поле потенциально, построим матрицу из всех 9

производных. В первом столбце по		x	, во втором по			y	и в 3-м по	z :
yz		0		z	y

xz	=	z		0	x
				x	0
xy		y		x	0

Матрица симметрична поле потенциально.

Теперь ищем потенциал. Для этого соединим начальную точку с произвольной с помощью ломаной, чтобы каждое звено было параллельно какой-либо из осей координат.

Начальная точка, как правило, (0,0,0). Изменяющуюся переменную при этом будем обозначать через t , чтобы отличать от переменных x ,

y ,	z , которые в этих вычислениях будут использять роль верхнего

предела в том или ином интеграле, либо роль фиксированной константы внутри функции. Получается такая сумма интегралов:

x	y	z
P(t,0,0)dt Q(x, t,0)dt R(x, y, t)dt
0	0	0

Применим это к конкретным функциям в этой задаче.

x	y	z
(0 0)dt (x 0)dt xydt
0	0	0

= 0

	0 xyt	z
	0 xyt	0
		0

xyz

Вспомнив, что потенциал определяется с точность до константы, окончательный ответ можно записать так: U xyz C .

Ответ. U xyz C .

Задача 25.	F (x	2	y	3	,	x	3	y	4	)

Решение. Найдём матрицу из всех производных:

x	2	y	3		2xy			3		3x	2	y	2


				=
	3	y	4		3x	2	y		4	4x	3	y	3
x

Матрица не симметрична. Тогда поле не потенциально. Ответ. Поле не потенциально.

Задача 26. F (3x 2 y 2 , 2x3 y) .

Решение. Найдём матрицу из всех производных:

6xy

Матрица симметрична. Поле потенциально.

Ищем криволинейный интеграл 2 рода по ломаной, соединяющей (0,0) с точкой (x, y) .

x	y	x				y							y
P(t,0)dt Q(x, t)dt		= (3t	2	0	2	)dt (2x	3	t)dt	= 0 x	3	t	2	y	=
			2		2		3			3		2
													0
0	0	0				0							0
0	0	0				0

Но потенциал вычисляется с точностью до константы, так что

x	3	y	2

U (x, y) x

C .

Ответ. U (x, y) x3 y 2 C .

Проверка.

C) x

C) y 2x

y .

Задача 27.

F ( y

2xy 2) .

Решение. Найдём матрицу из всех производных:

2 y

2xy 2

2 y

Матрица симметрична, значит, существует потенциал поля.

P(t,0)dt Q(x, t)dt

1)dt

(2xt 2)dt

x xy

2 y .

Ответ.

U (x, y) x xy

2 y C .

(x xy

Проверка.

(x xy

2y C) x 1

Задача 28.

F ( y

z,2xyz, xy

) .

Решение. Найдём производную матрицу.

2 yz

2xyz

2 yz

2xz

2xy

	t	x
	t	0
		0

2 y

    

xt	2

C) y

y	2t	y	=
		y
0		0
		0

2xy 2

Она симметрична, значит, поле потенциально. Ищем потенциал:

x	y	z
P(t,0,0)dt Q(x, t,0)dt R(x, y, t)dt =
0	0	0

0dt

(xy

)dt

0 0 xy

Ответ.

U xy

С .

Задача 29.

F (2xe

, x

) .

Решение.

Производная матрица симметрична:

2xe

Ищем потенциал поля.

xy	2	z

z	3

P(t,0)dt Q(x, t)dt

2te

)

Ответ.

U x

Задача 30.

(2e

2 x

sin y, e

2 x

cos y) .

2 x

sin

2 x

sin y

Решение.

2 x

cos y

dt	= t			2	x	x	2

					0

=	x	2	e	y	.

2e	2 x		cos y
2e			cos y

e		2 x
e			sin y

e	t	y	=

		0

симметрична.

x	y								x
P(t,0)dt Q(x, t)dt								= 2e				2t		sin
P(t,0)dt Q(x, t)dt								= 2e						sin
0	0								0
e2 x sin y .		Ответ.						U e2 x sin
					1		1		1
					1		1		1
Задача 31.	F					,		,		.
Задача 31.	F					,		,		.
							y		z
				x			y		z
			1								1
			1								1		x2
				x									x2
Решение.			1				=				0
				y
			1

											0
				z							0

	y							y
0dt		e	2 x	cos tdt	= 0 e	2 x	sin t	y


								0
	0							0
	0

y C .

0		0
0		0
1
1	y 2	0	симметрична.
	y 2	1
0		1
		z 2

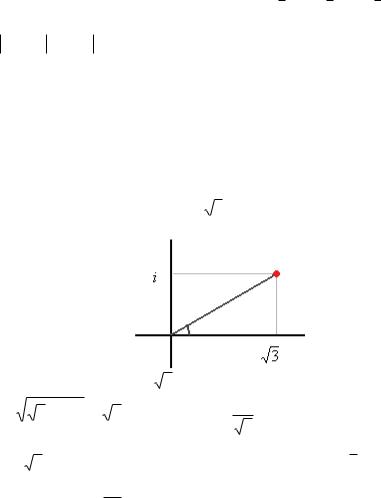
В данном случае мы не можем в качестве начальной точки взять (0,0,0), так как эти функции имеют там бесконечный предел. Однако можно рассматривать точку (1,1,1) .

P(t,0,0)dt Q(x, t,0)dt R(x, y,t)dt

ln t

= (ln x ln 1) (ln y

ln 1) (ln z ln 1)

ln x ln y ln z

ln( xyz) .

Ответ.

U ln( xyz) C .

Глава 2. Теория функций комплексного переменного. Действия над комплексными числами.

		18
Задача 32. Возвести в степень		3 i .
Решение. Чертёж:

Катеты имеют длину

3	2	2	4

		1

1	и		3	, поэтому в полярных коорданатах:

2		,	arctg		1		.
					3	6

Тогда

i

3 i 2e	6

в показательной форме, а тогда 3 i 18 =

	i		18
2e		6

			i	18
= 2	18	e	i	6
	18

18	e	i3
= 2	e

далее раскроем по формуле Эйлера:

218 (cos 3 i sin 3 ) , но синус и косинус не зависят от добавления и

вычитания полного оборота

, поэтому получается

18	(cos
2

Задача 33.

Решение.

i sin )	18	( 1 i0)	18
	= 2		= 2

Вычислить в показательной

. Ответ.
форме		3
	1

2	18

i	.

3i

Для 1-го числа:


		1		6
		1

(та же точка, как в прошлой задаче).

																															i
								2			2 ,		2					4								3 i			2e		i	6
																		4								3 i			2e

Для 2-го числа:																			.		Тогда							=			4			=

																		3						1 3i						i

																																3

																													2e
																													2e
			4				7							7									7											12
		6	3				6							7									7											12
	i				i					= cos							i sin								, прибавим 2
e				= e																															, для
e				= e																															, для
														6									6											6
удобства вычисления. Итак,																		5							5				3	i			1	.
удобства вычисления. Итак,																cos						i sin					=			i				.
																			6						6				2				2
																			6						6				2				2

Ответ.					3	i		1	.
Ответ.						i			.
				2				2
Задача 34.					Вычислить								(2 2i)10							.
												(					i)16
												(			3		i)16

Решение. Представим в показательной форме каждое из чисел.


		1		4
		1

				5
		2		6
		2

. Тогда



	10
(2 2i)		=
(2 2i)
(	16
	16
	3 i)

прибавили угол

			i		10
			i
2	2e			4
2	2e

						=
					16	=
		i	5		16
		i	5
	2e		6
	2e


8		, кратный
	4	, кратный
	4

		i	10							i
15		i		4					2	i
15
2	e					1	e
2	e				=	1	e				здесь в числителе
				80	=	2		8			здесь в числителе
			i	80			i	8
16			i	6			i		6
16
2		e					e
2		e					e
2	, а в знаменателе отняли											72	.
2	, а в знаменателе отняли											6	.
												6

									i											8										11
		1		e					i			1								8						1				11						1				i
		1		e				2				1						2			6	i				1				6		i				1	e			i
Далее,											=		e					2			6			=			e			6					=				6		=
Далее,		2					8				=	2	e											=		2	e								=	2					=
						i	8
				e		i		6
								6

1																1					3					1				3					1
1																1					3					1				3					1
	cos			i sin									=										i					=								i .
	cos			i sin									=										i					=								i .
2		6									6					2					2					2				4					4



Ответ.			3						1	i .
Ответ.		4							4	i .
		4							4
																										(		3		3i)			6									27
Домашняя задача.														Вычислить												(		3		3i)					. Ответ.							27	i
Домашняя задача.														Вычислить												( 1 i)					18				. Ответ.						8		i
																															18

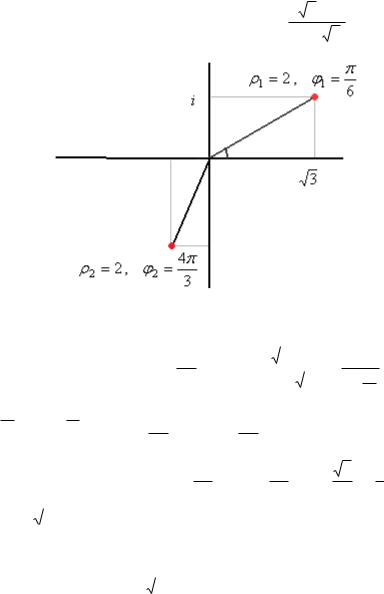
Задача 35.								Вычислить											4		2 2							3i
Задача 35.								Вычислить													2 2							3i
															n						n							2 k						i sin				2 k
Решение.					Формула:										n		z				n				cos
Решение.					Формула:												z								cos
																													n												n

Сначала найдём модуль и аргумент исходного числа.

 

2 (т.к. 90 градусов и ещё 30 во второй четверти),

			4 4 3								16 4 .
				n				n				2 k						2 k
Тогда				n	z			n	cos					i sin							=
Тогда					z				cos					i sin							=
													n						n
									2		2 k				2
										3	2 k				3				2 k
4	z	4		4			cos			3		i sin			3					=
	z			4			cos				4	i sin					4			=
											4						4


										k									таким образом, 4 точки лежат на
	2 cos									k	i sin					k			таким образом, 4 точки лежат на
						6			2				6		2
						6			2				6		2

окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня:

k 0	:
k 1:
k 2	:
k 3	:

Чертёж:


2 cos



2 cos



2 cos



2 cos

					=
i sin
6		6

4		4
	i sin
6			6

7		7
	i sin
6
			6
11			11
		i sin
6				6

				3			1				3						1
	2			3	i		1			=	3		i				1	.

			2				2				2						2



					1					3				1					3
=		2			1	i				3	=			1			i		3		.

					2				2
															2				2



						3				1							3		1
=		2				3		i		1	=						3	i	1

						2				2							2		2





					1					3		1						3
					1					3		1						3
	=		2			i					=					i				.
	=		2			i					=					i				.
					2				2
					2				2			2						2

			3			1
Ответ.			3	i		1				и
Ответ.				i						и
			2				2
			2				2

Задача 36.			Дано				z			2 i
Задача 36.			Дано				z			2 i		6
												6
			2 i						i
			2 i	6	= e			2	i	6	= e		2
Решение.		e			= e			2	e		= e		2

			3			1
Ответ. e	2			i					.
Ответ. e			2	i		2			.

1	i	3
2		2

. Найти e

		i
cos		i
	6


		.
		.

z
.
sin
sin
	6

e		3
e	2
		2
		2

i	1
i
	2
	2

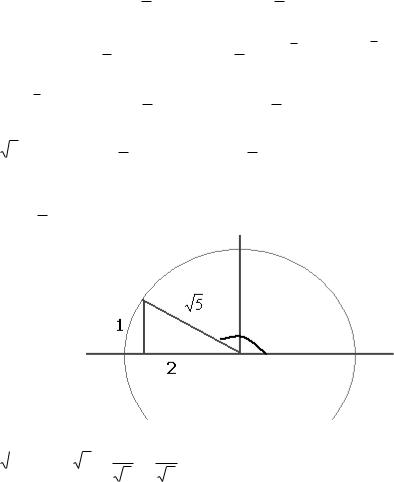
Задача 37. Дано z ln

40 i arctg(3) . Найти e

Решение.

ln 40 i arctg(3)

i arctg(3)

40 cos(arctg3) i sin( arctg3) .

Далее с

помощью

прямоугольного

треугольника

вычислим

cos(arctg3), sin( arctg3) .

Если надо

найти

синус и косинус того угла, тангенс которого равен 3, то сначала

подпишем длины катетов по известному тангенсу, гипотенуза

вычислится автоматом по теореме Пифагора, а далее будет уже известны синус и косинус.

40 cos(arctg3) i sin( arctg3) =

Ответ. 2 6i .

	1		3
	1		3
40		i		=
40		i		=
	10		10
	10		10

2 6i

Задача 38. Дано

z	1
z		ln 5 i
	2

arctg

1 2

 

. Найти

e	z

						1						1			1				1
						1						1				ln 5		i arctg
Решение.					exp			ln 5 i arctg					= e		2		e		2
															2				2
							2
							2					2
		1							1					1
e	ln 5					arctg			1		arctg			1		=
e			2	cos		arctg				i sin	arctg					=
			2
									2					2
									2					2

	1		arctg	1
5 cos arctg		i sin	arctg
	2
	2			2

. Делаем аналогично тому,

как в прошлой задаче,

arctg	1	отмеряется от
	2

просто треугольник здесь во 2 четверти (угол

180 в обратном направлении).

Но гипотенуза всё равно легко вычисляется по теореме Пифагора:

			2	i	1	= 2 i .
	5 , тогда		2		1
	5 , тогда	5
			5		5
			5		5
Ответ. 2 i .
Задача 39.		Найти все значения					Ln(e)

Решение. Используем формулу Ln(z)

Ln(e) ln e i( 2k) = 1 i( 2k)

комплексной плоскости, имеющие вид:

Ответ. 1 i( 2 k) .

ln i( 2 k) .

. Таким образом, это точки в

1 i , 1 i3 ,1 i5 , ...

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20232.61 Mб4Математика.-2.pdf
#
05.02.20232.05 Mб3Математика.-3.pdf
#
05.02.20232.49 Mб3Математика.-4.pdf
#
05.02.20233.03 Mб3Математика.-5.pdf
#
05.02.20232.78 Mб3Математика.-6.pdf
#
05.02.20232.74 Mб5Математика.-7.pdf
#
05.02.20233.16 Mб4Математика..pdf
#
05.02.2023584.83 Кб53Математическая логика и теория алгоритмов.-1.pdf
#
05.02.2023886.2 Кб7Математическая логика и теория алгоритмов.-2.pdf
#
05.02.2023671.92 Кб5Математическая логика и теория алгоритмов.-3.pdf
#
05.02.2023482.94 Кб5Математическая логика и теория алгоритмов.-4.pdf

				3			1				3						1
	2			3	i		1			=	3		i				1	.

			2				2				2						2



					1					3				1					3
=		2			1	i				3	=			1			i		3		.

					2				2
															2				2



						3				1							3		1
=		2				3		i		1	=						3	i	1

						2				2							2		2





					1					3		1						3
					1					3		1						3
	=		2			i					=					i				.
	=		2			i					=					i				.
					2				2
					2				2			2						2

				3			1				3						1
	2			3	i		1			=	3		i				1	.

			2				2				2						2



					1					3				1					3
=		2			1	i				3	=			1			i		3		.

					2				2
															2				2



						3				1							3		1
=		2				3		i		1	=						3	i	1

						2				2							2		2





					1					3		1						3
					1					3		1						3
	=		2			i					=					i				.
	=		2			i					=					i				.
					2				2
					2				2			2						2

				3			1				3						1
	2			3	i		1			=	3		i				1	.

			2				2				2						2



					1					3				1					3
=		2			1	i				3	=			1			i		3		.

					2				2
															2				2



						3				1							3		1
=		2				3		i		1	=						3	i	1

						2				2							2		2





					1					3		1						3
					1					3		1						3
	=		2			i					=					i				.
	=		2			i					=					i				.
					2				2
					2				2			2						2