Математика.-7

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

cos2 t sin 2 tdt sin 2 t cos tdt =

(2 cos t sin t)2 dt sin 2 t d (sin t)

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.74 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

45sin

0 30 sin

15cos

15(sin

18sin t cos t 50sin t cos

cos2 t) 32 sin t cos t dt

t dt

0
		1 cos 2t
	30	1 cos 2t
	30		15 16 sin 2t dt
0		2
0


15	dt 16 sin 2tdt 15 1 cos 2t dt
0	0	0

						15
= 15t		8cos 2t		15t			sin 2t
	0		0		0	2

							0

30 . Ответ. 30 .

= 15 8(1 1) 15 152 (0 0) =

В следующих задачах кривые будут замкнутые, и в них будем применять формулу Грина, доказанную на лекции:

			Q	P
	Pdx Qdy
	Pdx Qdy			dxdy.
L		D	x	y

Наиболее удобно её применение именно в тех случаях, когда граница состоит из нескольких частей, ведь работу векторного поля надо было бы отдельно вычислять по каждой части (у которой своё уравнение в плоскости), а двойной интеграл сразу по единой плоской области.

Задача 15.

Найти циркуляцию векторного поля F x2 y, y 2 по перемещению

точки по границе верхнего полукруга радиуса 1 двумя методами: А). без формулы Грина. Б). по формуле Грина.

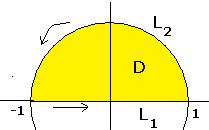
Решение.

Решение А). без формулы Грина. В этом случае нужно для каждого участка - отрезка L1 и полуокружности L2 - вычислить работу поля

отдельно. Чтобы обход всего контура осуществлялся один раз и

против часовой стрелки, надо, чтобы движение по отрезку было слева направо x [ 1,1] (при этом y 0 , и dy 0 ), а по

полуокружности справа налево, т.е. на ней использовать обычный метод параметрического задания точек: x cos t, y sin t .

По L1

По L2 :

cos2

1
		x	2	0dx			= 0.
			2

1
	(cos									t) cos t dt
					2	t sin t)( sin t) (sin			2		=
					2				2

0

t sin 2 tdt sin 2 t cos tdt ,								во втором интеграле очевидно,
						0

подведение под знак дифференциала, а в первом есть несколько путей решения:

1)с помощью замены, учитывая то, что суммарная степень чётна (изучали во 2 семестре).

2)применить формулу понижения степени к каждому из квадратов.

3) использовать то, что (sin t cos t) Наиболее оптимальным наверное,

и формулу sin 2t 2sin t cost .

здесь будет 3-й путь.

		1						1									1
=			sin	2	2tdt					sin	3	t			=
=		4	sin		2tdt			3		sin		t	0		=		4
		4	0					3									4	0


	1										1					1
	1	(1 cos 4t)dt						=			1					1
		(1 cos 4t)dt						=				t		0			sin
	8	0									8					4
	8										8					4

Решение Б). По формуле Грина.
Если			F x			2	y, y	2	то			Q				P
						2		2
												x				y
												x				y

1 cos
		2
4t
	0


0 x			2

4t	dt
	dt
=
.

1 (0 0)

Двойной интеграл по полукругу вычисляется с помощью полярных координат, это стандартная задача, которые решали во 2 семестре. Так как полукруг в верхней полуплоскости, то [0, ] , а радиус 1,

[0,1].

		x		2	dxdy	=
				2

D
			cos 2
	1		cos 2
					2
0					2
0

d 4

										1
( cos )			2	d =		cos	2	d			3	d
			2				2				3

					0					0
1	1								1
	1	1		cos 2 d					1
=		1		cos 2 d				=			0
0	8	0							8
	8								8

1	sin 2
2	sin 2	0
		0

 

=	1	1		=		.
=			(0 0)	=		.
	8	2			8
	8	2			8

Ответ. 8 .

Задача 16.

Найти циркуляцию векторного поля F x 2 y 3 ,1 по перемещению

точки по треугольнику с вершинами (0,0), (0,1), (1,1) с помощью формулы Грина.

Решение. Если не использовать формулу Грина, то на каждой из сторон - горизонтальной, вектикальной и наклонной - надо было бы отдельно провести вычисление работы поля. Используя формулу Грина, мы вычислим лишь один двойной интеграл.

	x 2 y 3 ,1	Q	P	0 3x2 y 2 .
F
		x	y

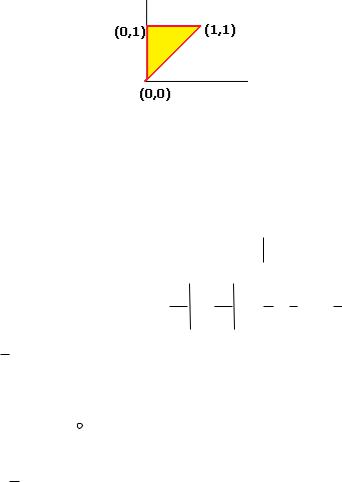
Чертёж этого треугольника:

Далее следует стандартный метод вычисления двойного интеграла, изученный в прошлом семестре. Сначала спроецируем фигуру на ось Ох и найдём глобальные границы по x , это x [0,1] . При каждом

конкретном									x		высота				изменяется								от наклонной										линии
горизонтальной											y 1		, то есть							y [x,1]				. Итак,
												1			1									1							1		1
3x		2		y		2	dxdy			=		dx 3x					2	y	2	dy	=			dx x				2	y	3	1	=	x		2
		2				2											2		2									2		3					2
	D											0			x									0							x		0
	D											0			x									0									0
	1											1										6	1			3	1
	x								dx		= x							dx =			x	6			x	3					1	1		1
=			2		x			5						5	x	2					x				x				=		1	1	=	1
			2					5						5		2
																					6				3						6	3		6
	0											0									6		0		3		0				6	3		6
	0											0

(1 x

x
3	)
	)

до

Ответ.	1	.
	6

Задача 17.

Найти циркуляцию

(1 x	2	) ydx (1 y	2	)xdy
(1 x		) ydx (1 y		)xdy
L

где L - это граница

четверти круга радиуса 1 (лежащего в

Решение. F (1 x2 ) y, (1 y 2 )x

1-й четверти).
Q	P	(1 y	2	) (1 x	2	)

x	y

x	2

y	2

. Если бы мы не применяли формулу Грина, то пришлось бы 3

раза вычислять работу силы по трём разным участкам, из которых состоит этот замкнутый контур: часть окружности, горизонтальный и вертикальный отрезки. Чертёж:

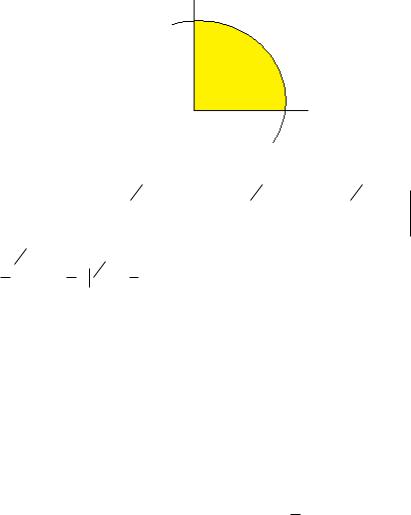
А по формуле Грина надо найти двойной интеграл по четверти круга, с очевидным переходом к полярным координатам.

												1
(x			y			)dxdy =				2		1			d
(x		2	y		2	)dxdy =				d				2	d
		2			2									2
D										0		0
1					1					1
1	2				1					1
	d			=				2	=			= .
	d			=			0		=			= .

4	0				4					4	2		8
	0

	1
2	1
d		3	d
d			d
0	0

2	4	1
= d			=
= d			=
	4
0		0

Ответ.

Контрольная работа

(30 минут, по 15 минут на задачу).

Задача 1. Тройной интеграл в сферических координатах. Задача 2. Криволинейный интеграл 1-го рода.

Практика № 4.

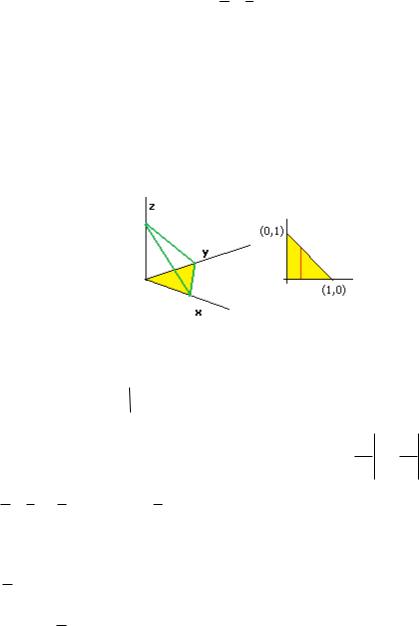
Поверхностные интегралы 2 рода (поток поля через поверхность). Задача 18. Найти поток векторного поля F (x z, y, y z) через

часть плоскости

z 1 x y

в 1-м октанте.

Решение. Данная поверхность это треугольник с вершинами (1,0,0), (0,1,0) и (0,0,1). При этом очевидно, что

f (1 x y)
x	x

, а также

f (1 x y)		1 .
y	y

Воспользуемся формулой

F , dS S

	x
	P f Q
D

f
	y

R dxdy

При этом ещё и повсеместно

(x (1 x y)) ( 1) y

z представим в виде 1 x ( 1) ( y (1 x y)) dxdy

3x 4 y

2 dxdy

, где D

- проекция исходного треугольника на

плоскость, плоскости,

т.е. треугольник с вершинами ограниченный сверху линией

(0,0),

y 1 x

(1,0) и (0,1) в (см. такой же

треугольник в задаче 10).

		3x 4 y 2 dxdy												1	1 x
Тогда		3x 4 y 2 dxdy											=	dx (3x 4 y 2)dy						=
		D												0	0
1						2							1					2
						2				1 x		= 3x(1 x) 2(1 x)						2	2(1 x) dx
dx 3xy 2 y								2 y		1 x														=
dx 3xy 2 y								2 y																=
0										0			0
0													0
1																1						2	1		3	1
3x 3x															2x dx	= x x		dx			x	2		x	3
				2	2		2x		2	4x 2							2			=	x			x
				2					2								2
																					2			3
0																0					2		0	3		0
0																0

1	1	=	1		.		Ответ.				1	.
2	3	=	6		.		Ответ.				6	.
2	3		6								6

Аналогично прошлой задаче, но с другим векторным полем: Задача домашняя Д-2. Найти поток векторного поля

F (2x 2 , x 2 y 2 , z y) через поверхность

Ответ. 12 .

z 1 x y

в 1 октанте.

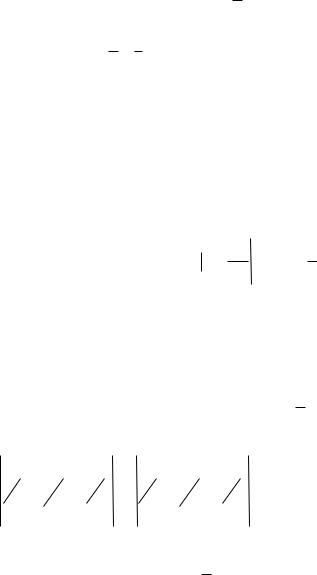
Задача 19. Найти поток векторного поля

F (x, y,3z)

через

поверхность

z x

, где

z [0,1].

f x

Q f y R dxdy .

Решение. Формула:

F , dS

= P

Здесь

f x

)x 2x ,

f y (x

) y 2 y .

) dxdy =

P f x

Q f y

R dxdy =

x 2x y 2 y 3(x

dxdy , причём D это проекция параболоида на плоскость

0ху, то есть D круг радиуса 1. Делаем обычный переход к полярным координатам для такого круга, как в прошлом семестре.

x				dxdy =	2	1				2
	2	y	2		d		2	d	=	2
		y			d			d	=	0

D					0	0

Ответ. 2 .

Ротор, дивергенция. Формулы Стокса, их применение.

	4	1	1

		= 2		=		.
4			4		2
		0

Остроградского-Гаусса и

Задача 20. Решение.

Вычислить дивергенцию и ротор поля

			y z 0	= y z .
divF Px	Qy Rz =			= y z .

(xy,

yz,

rot(F) =

Ответ.

	i
	x
	x
	P
divF

	j
	y

Q
y z

	k			i		j	k
	z	=		x		y	z
	z	=		x		y	z
R			xy		yz		x

, rotF y, 1, x .

y, 1,

Задача 21. Найти циркуляцию поля F (xy, yz, x) по треугольнику с

вершинами (1,0,0), (0,1,0), (0,0,1).

Решение. Если вычислять без формулы Стокса, то надо найти 3 раза работу поля по 3 различным сторонам треугольника.

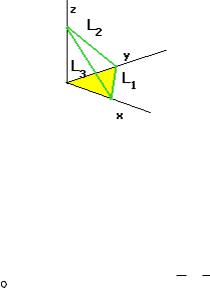
Например, можно на каждой стороне описать движение точки с помощью параметра t так:

на	L1	:	x 1 t, y t, z 0	,
на	L2	:	x 0, y 1 t, z t	,
на	L3	:	x t, y 0, z 1 t .

Но по формуле Стокса мы можем не делать 3 разных вычисления работы поля, а вычислить через двойной интеграл по единой области.

Формула Стокса.

Pdx Qdy Rdz

(rotF , dS ) S

Для этого векторного поля, ротор был найден в задаче 20: rotF y, 1, x .

Нужно найти поток через данный треугольник, как в задаче 18, но не самого векторного поля, а ротора (нового векторного поля,

полученного с помощью исходного).						R dxdy где
Вычислим интеграл
Вычислим интеграл			P f x Q		f y

		D
		,				1 , а	P, Q, R это компоненты
f x (1 x y) x 1		,	f y (1	x y) y		1 , а	P, Q, R это компоненты
ротора, т.е. векторного поля y, 1, x ,
				( y) ( 1) ( 1) ( 1) x dxdy =
P f x	Q f y R dxdy =			( y) ( 1) ( 1) ( 1) x dxdy =
D				D
						1	1 x
y 1 x dxdy =		x y 1 dxdy = dx (x y 1)dy =

	1					1
dx				xy		1	y		2
									2
						2
	0					2
	0
	1						1
					2		1	(1
x x								(1
	0						2
	0
1	1						3
	1	x	2	x			3
		x		x					dx
0	2						2
0

	1 x					1
				=
y								x(1
y								x(1

	0					0
	0
x	2	2x)
x		2x)				1 x dx

		x	3	1	x		2	1	3
			3				2
=
=		6				2			2
		6		0		2		0	2
				0				0

x)		1
x)		2
		2
		1
=
=
		0
1
x	=
0

(1 x)				2

	3		1		x	2

	2		2
1		1			3
6		2			2


	x)


	x dx

		5
		6
		6

Ответ.	5	.
Ответ.	6	.
	6
Задача 22. Найти поток поля			F (x	2	yz, x y, xyz)	через поверхность
Задача 22. Найти поток поля			F (x		yz, x y, xyz)	через поверхность

куба	x, y, z [0,1] .

Решение. Если не использовать формулу Остроградского-Гаусса:

(F , dS ) div(F )dxdydz
S	D

то нужно было бы вычислить 6 раз поток поля (через каждую грань поверхности куба). А по формуле Остроградского-Гаусса будет всего лишь одно вычисление тройного интеграла по внутренности куба.

Во-первых,				divF 2xyz 1 xy .
											1		1	1
Тогда div(F )dxdydz										= dx dy (2xyz xy 1)dz									=
		D									0		0	0
1	1											1	1				1
				2	xyz z				1		= dx 2xy 1 dy					=	dx xy			2	y	1
dx dy xyz					xyz z						= dx 2xy 1 dy					=	dx xy				y
0	0								0			0	0				0					0
									0													0

1					x	2	1				1			3			3
1						2		1
(x 1)dx			=				x	1	=			1 =			. Ответ.			.
								0
					2			0			2			2			2
0					2		0				2			2			2
0

Задача 23. Найти поток поля	F (x	2	,2y, z)

ограниченную эллиптическим параболоидом плоскостью z 1.

через поверхность, z x2 y 2 и

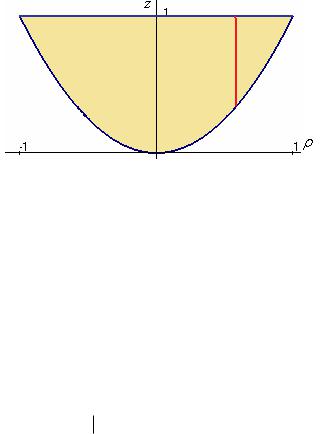
Решение.

Снова воспользуемся формулой Остроградского-Гаусса. Иначе пришлось бы вычислять 2 потока поля: по параболоиду и кругу.

divF 2x 3

Построим вертикальное сечение проходящее через ось Oz , причём неважно, в какую сторону оно повёрнуто: для тела вращения, диапазон изменения z зависит только от (расстояния от оси Oz ),

но не зависит горизонтальную

от


угла	. Поэтому			так	и	обозначим	оси:
вертикальную		z	.	Так	как	в сечении	снизу

парабола а сверху прямая линия на уровне 1, то	z [	2

на горизонтальную плоскость - круг радиуса 1. Поэтому

,1]

. Проекция

2	1	1
d d (3 2 cos)dz
0	0		2

. Обратите внимание, что

divF 2x 3

мы

тоже выразили в полярных координатах. Сначала применим формулу

Ньютона-Лейбница по						z	, получается:
Ньютона-Лейбница по							, получается:
2		1									2	1
d d (3 2 cos )z							1			=	d (3 2 cos)(1		2	) d	=
													2
							2
0		0									0	0
2		1	3(						) cos d
	d			3	) 2(			3				, разобьём на 2 интеграла: здесь
				3				3

0		0

в первом слагаемом нет

, а во

вынести множитель, зависящий от

2 1	2	1
d 3( 3 ) d cos		d 2 (

втором есть, там можно будет

3 ) d =

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20232.61 Mб4Математика.-2.pdf
#
05.02.20232.05 Mб3Математика.-3.pdf
#
05.02.20232.49 Mб3Математика.-4.pdf
#
05.02.20233.03 Mб3Математика.-5.pdf
#
05.02.20232.78 Mб3Математика.-6.pdf
#
05.02.20232.74 Mб5Математика.-7.pdf
#
05.02.20233.16 Mб4Математика..pdf
#
05.02.2023584.83 Кб53Математическая логика и теория алгоритмов.-1.pdf
#
05.02.2023886.2 Кб7Математическая логика и теория алгоритмов.-2.pdf
#
05.02.2023671.92 Кб5Математическая логика и теория алгоритмов.-3.pdf
#
05.02.2023482.94 Кб5Математическая логика и теория алгоритмов.-4.pdf